3001. 捕获黑皇后需要的最少移动次数
题目
现有一个下标从 0 开始的 8 x 8 棋盘,上面有 3 枚棋子。
给你 6 个整数 a 、b 、c 、d 、e 和 f ,其中:
(a, b)表示白色车的位置。(c, d)表示白色象的位置。(e, f)表示黑皇后的位置。
假定你只能移动白色棋子,返回捕获黑皇后所需的最少移动次数。
请注意:
- 车可以向垂直或水平方向移动任意数量的格子,但不能跳过其他棋子。
- 象可以沿对角线方向移动任意数量的格子,但不能跳过其他棋子。
- 如果车或象能移向皇后所在的格子,则认为它们可以捕获皇后。
- 皇后不能移动。
示例 1:
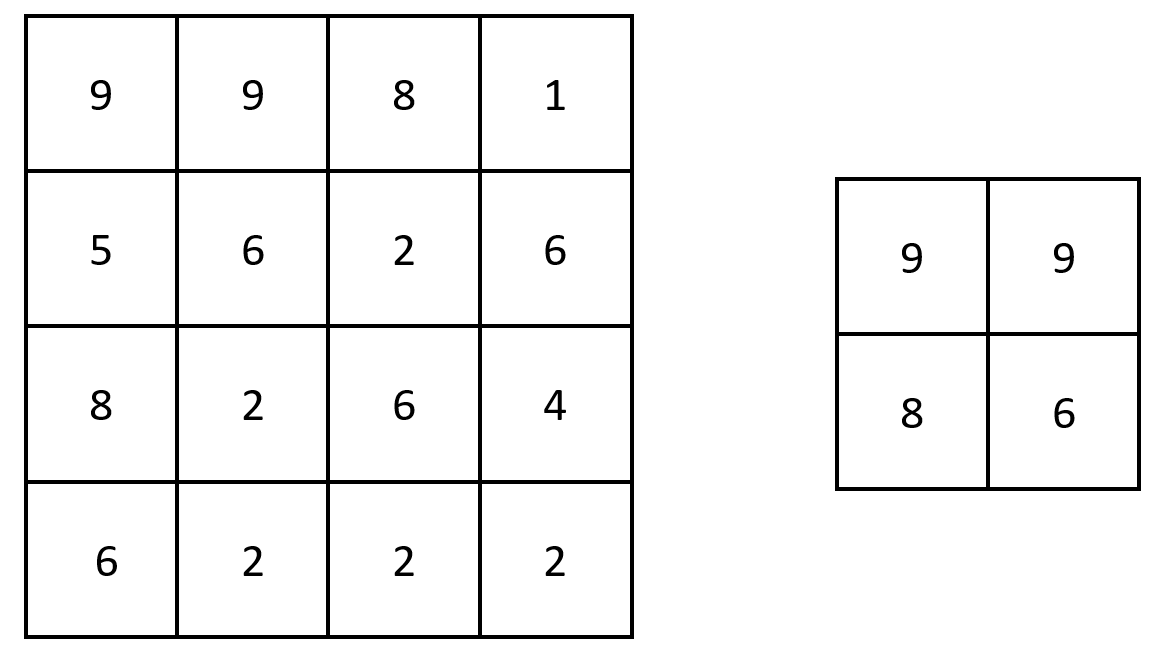
输入:a = 1, b = 1, c = 8, d = 8, e = 2, f = 3
输出:2
解释:将白色车先移动到 (1, 3) ,然后移动到 (2, 3) 来捕获黑皇后,共需移动 2 次。
由于起始时没有任何棋子正在攻击黑皇后,要想捕获黑皇后,移动次数不可能少于 2 次。示例 2:
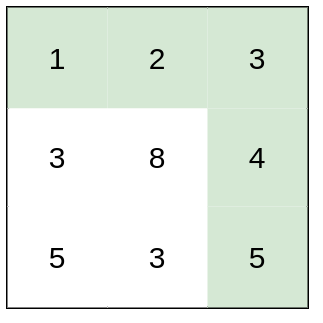
输入:a = 5, b = 3, c = 3, d = 4, e = 5, f = 2
输出:1
解释:可以通过以下任一方式移动 1 次捕获黑皇后:
- 将白色车移动到 (5, 2) 。
- 将白色象移动到 (5, 2) 。提示:
1 <= a, b, c, d, e, f <= 8- 两枚棋子不会同时出现在同一个格子上。
解答
思路
直接攻击:
- 白车可以直接攻击到黑后
- 白象可以直接攻击到黑后
如果不能直接攻击到,那么一定只需要 2 步即可:
- 车被象挡住了,那么移开白象即可
- 没有被挡住,那么白车一定可以两步内攻击到黑后(一步将军)总有一个方向不会被挡住
所以只需要判断是否能直接攻击即可,以及是否被挡住的情况。
第一个数字是行,第二个数字是列。
代码
python
class Solution:
def minMovesToCaptureTheQueen(self, a: int, b: int, c: int, d: int, e: int, f: int) -> int:
def not_inside(left: int, mid: int, right: int) -> bool:
return not min(left, right) < mid < max(left, right) # 象不在中间
if a == e and (c != e or not_inside(b, d, f)) or \
b == f and (d != f or not_inside(a, c, e)) or \
c + d == e + f and (a + b != e + f or not_inside(c, a, e)) or \
c - d == e - f and (a - b != e - f or not_inside(c, a, e)):
return 1
return 2