98. 验证二叉搜索树
题目
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3]
输出:true示例 2:
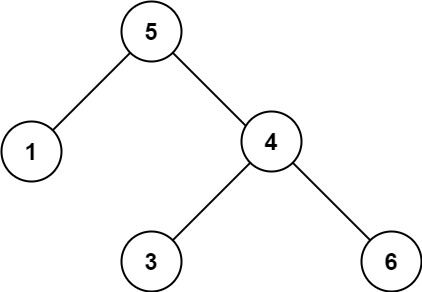
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。提示:
- 树中节点数目范围在
[1, 10^4]内 -2^31 <= Node.val <= 2^31 - 1
解答
思路:前序遍历
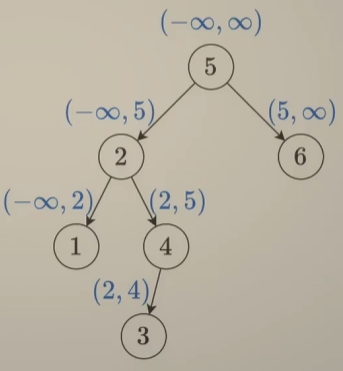
二叉搜索树:
- 左子树都小于根节点:左子树的值区间为
(-inf, 5) - 右子树都大于根节点:右子树的值区间为
(5, +inf) - 对于 4 而言,它的区间经过累计计算后为
(2, 5),也就是祖先的最小值和最大值
递归时除了传入结点 node,还需要传入开区间的范围:对于每个节点值,先判断它的 val 是否在开区间内,然后再往下递归:往左递归就更新开区间的右边界值,往右递归就更新开区间的左边界值。这种先访问节点值,再递归左右子树的做法叫做 前序遍历。
注意:根节点传入 (-inf, inf) 即可。
代码
Python 代码
python
class Solution:
def isValidBST(self, root: Optional[TreeNode], left=-inf, right=inf) -> bool:
if root is None:
return True
x = root.val
return left < x < right and \
self.isValidBST(root.left, left, x) and \
self.isValidBST(root.right, x, right)思路:中序遍历
如果按照先遍历左子树,再遍历根节点,最后遍历右子树的方式,我们遍历 二叉平衡树 就会得到一个严格递增的数组。可以用数学归纳法证明(因为 BST 始终有左子树 < 根节点 < 右子树)。
如何验证数组是严格递增的?比较相邻的数字即可。在二叉树中,比较当前的节点值是否大于上一个节点值,然后把节点值记录下来方便后续比较。第一个节点没有前驱,可以将其初始化为 -inf。
代码
Python 代码
python
class Solution:
pre = -inf
def isValidBST(self, root: Optional[TreeNode]) -> bool:
if root is None:
return True
if not self.isValidBST(root.left):
return False
if root.val <= self.pre:
return False
self.pre = root.val
return self.isValidBST(root.right)思路:后序遍历
我们还可以把节点值的范围往上传:
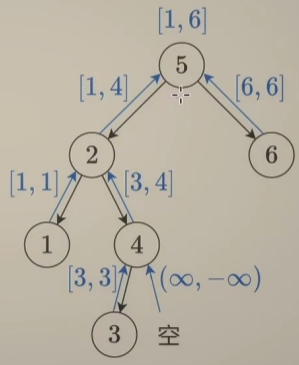
以 5 为例,它左子树的范围是 [1, 4],右子树的范围是 [6, 6]。那么由于 5 大于左边的最大值,小于右边的最小值,因此 5 这个值是合理的。这种做法需要先遍历左右子树,得到范围,再判断根节点和范围的关系,被称为 后序遍历。
注意:并不是左边只需要返回最大值才行,左子树的最大值用于和根节点比较,左子树的最小值用于范围框定,右子树同理。最小值和最大值都需要返回。递归到空节点时,可以返回 (inf, -inf),这样通过空节点对于 BST 的判断就一定不成立。
最后如果返回的结果是 (-inf, inf),说明不是 BST。
代码
Python 代码
python
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
def f(node):
if node is None:
return inf, -inf
l_min, l_max = f(node.left)
r_min, r_max = f(node.right)
x = node.val
if x <= l_max or x >= r_min: # (inf, -inf) 一定保证它不成立
return -inf, inf
return min(l_min, x), max(r_max, x)
return f(root)[1] != inf