78. 子集
题目
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]示例 2:
输入:nums = [0]
输出:[[],[0]]提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
解答
思路:顺序视角
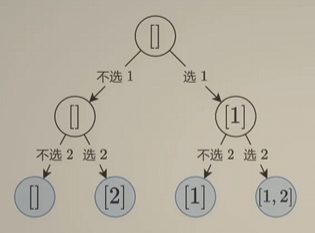
子集型回溯:对于集合的每个元素,都有选/不选两种操作。
我们以 [1, 2] 的子集个数来思考。站在 输入 的角度:枚举第
回溯三问:
- 当前操作:枚举第
个数,选还是不选, dfs(i) - 当前问题:从下标
的所有集合元素中构造子集 - 当前问题的子问题:从下标
的数字中构造子集
注意边界条件和非边界条件。
- 时间复杂度为
- 空间复杂度为
代码
python
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
ans = []
path = []
n = len(nums)
def dfs(i):
if i == n:
ans.append(path.copy()) # path 是个全局变量,每次都在变化,加入深拷贝
return
dfs(i + 1) # 不选
path.append(nums[i])
dfs(i + 1) # 选
path.pop() # 恢复现场
dfs(0)
return ans所谓的恢复现场就是:从一个分支转移到另一个分支的过程。至于 dfs(i) 可以理解为当函数执行完毕后,从下标
思路:答案视角
站在答案的视角:
- 空集什么都不选
- 枚举第一个数选什么
- 枚举第二个数选什么
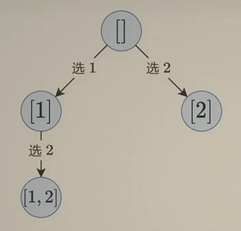
注意:由于 [1, 2] 和 [2, 1] 是相同的子集。因此我们可以规定一个 严格递增 的顺序,即后选的数要比先选的数要大。此时,每个节点都是答案。
回溯三问:
- 当前操作:枚举一个下标
的数字,加入 path - 当前问题:从下标
的集合所有数字中构造子集 - 它的子问题:从 下标
的数字中构造子集
于是在 递归树 中,dfs(i) 的子节点为 dfs(i + 1), dfs(i + 2), ..., dfs(n)
代码
python
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
ans = []
path = []
n = len(nums)
def dfs(i):
ans.append(path.copy()) # 每个节点都是答案
if i == n:
return
for j in range(i, n):
path.append(nums[j])
dfs(j + 1)
path.pop()
dfs(0)
return ans