104. 二叉树的最大深度

题目

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

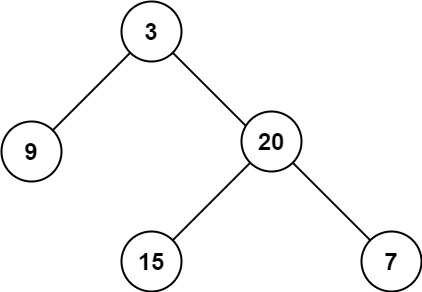
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 10^4] 区间内。
• -100 <= Node.val <= 100

解答

思路

最大深度的定义：根节点到最远叶子节点的最长路径上的节点个数。

对于二叉树问题，不要一上来就陷入数学上的计算细节，而是思考 整棵树和其左右子树 之间的关系，比如问题能否转换成左右子树的子问题，或者说：已经知道了左右子树的最大深度，如何求出整棵树的最大深度。显然：

$$\text{depth}=max({\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{h}}_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}},{\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{h}}_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}})+1$$

注意到：

• 原问题：计算整棵树的最大深度
• 子问题：计算左右子树的最大深度
• 子问题和原问题是类似的

类比循环，循环执行的是同一份代码，而这种相似的问题，自然也是使用同一份代码。唯一的区别就是：子问题需要 把计算结果返回给上一级问题，更适合用 递归 实现（循环是把计算结果返回给一个循环外的变量）。

由于子问题的规模比原问题小，因此不断执行下去，总会有个尽头，即递归的 边界条件 base case，此时问题是平凡的，我们可以直接返回这个子问题的答案（子问题再经过计算后把计算结果返回它的上一级问题）。

由于每个节点我们都只遍历了一次，因此：

• 时间复杂度为 $O(n)$
• 空间复杂度为 $O(n)$

我们子问题在返回的时候，它怎么知道把计算结果 return 到内存的什么位置上呢？计算机在执行递归的时候会把递归调用者的位置保留下来，可以理解为数组，但实际上是通过 栈 来实现的，由于计算需要遍历所有节点，因此每个节点都会被计算机保留下来，等到它们的 下一级计算出结果 返回后，它们再计算后返回它的上一级节点。

TODO：这里一定是最坏情况（一条左子树链）才是 $O(n)$ 的吗？当然这种情况下栈的大小一定是 $n$ 的。

代码

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        
        l_depth = self.maxDepth(root->left)
        r_depth = self.maxDepth(root->right)

        return max(l_depth, r_depth) + 1

思路：传递路径上的节点个数

递归过程中，也可以向下一级传递信息。例如这里可以每个节点可以把 从根节点到你这里经过的节点个数 这个信息传递下去。递归边界是空节点，此时每个叶子节点上都有一个值，只需要取这些中的最大值就可以得到 最大深度，可以用一个全局变量来维护，每次 +1 后都更新：

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        ans = 0

        def f(node, cnt):
            if node is None:
                return
            
            cnt += 1
            nonlocal ans
            ans = max(ans, cnt)

            f(node.left, cnt)
            f(node.right, cnt)
        
        f(root, 0)
        
        return ans