77. 组合

题目

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

解答

思路

回顾从 [3, 2, 1] 中选出所有子集的搜索树：

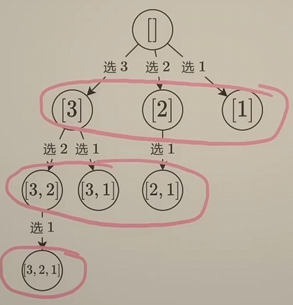
可以看出：每一层的子集长度是一样的，因此从 $n$ 个数中选 $k$ 个数的组合问题可以看作是 长度固定的子集。

两种剪枝方法：

• 如果选择长度为 2 的子集，那么递归到长度为 2 就可以直接返回
• 如果选择长度为 3 的子集，那么递归到数字 2 时就可以直接返回，因此剩余的数字不够组成长度为 3 的子集

设路径当前长度为 $m$，还需要选择 $d=k-m$ 个数。由于是从大到小枚举，设当前需要从 $[1,i]$ 中选择，如果 $i<d$，那么最后无法选出 $k$ 个数，不需要进一步递归，直接 剪枝。

代码

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        ans = []
        path = []

        def dfs(i):
            d = k - len(path)
            if i < d:
                return

            if len(path) == k:
                ans.append(path.copy())
                return

            for j in range(i, 0, -1): # (i, d - 1, -1)
                path.append(j)
                dfs(j - 1)
                path.pop()
            
        dfs(n)

        return ans

如何计算 回溯的时间复杂度？我们把每个叶子都拆开看，也就是每个叶子的计算时间是从根到叶子这一条路径上的计算时间，由于路径上基本上时间都是 $O(1)$，因此总的时间复杂度为 叶子个数乘以路径长度。

• 时间复杂度 $O(k{C}_n^k)$
• 空间复杂度 $O(k)$

思路：选或不选

代码

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        ans = []
        path = []
        
        def dfs(i: int) -> None:
            d = k - len(path)  # 还要选 d 个数

            if d == 0:
                ans.append(path.copy())
                return
            
            # 不选 i
            if i > d:
                dfs(i - 1)
            
            # 选 i
            path.append(i)
            dfs(i - 1)
            path.pop()
        
        dfs(n)
        return ans