543. 二叉树的直径

题目

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

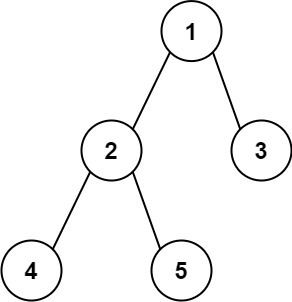
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

• 树中节点数目在范围 [1, 10^4] 内
• -100 <= Node.val <= 100

解答

思路

首先我们知道：树的直径对应的路径 起点和终点一定是叶子节点，否则我们可以继续延伸到叶子节点，从而得到一个更长的路径。

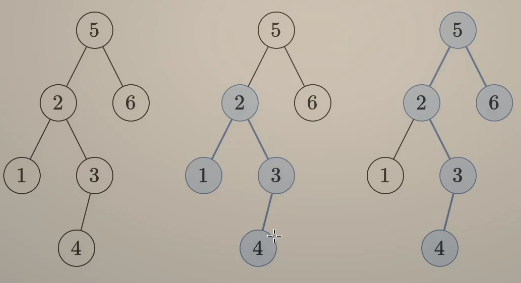
通过观察我们发现：直径 一定会在树的某个节点拐弯，也就是在某个节点处，直径左边在它的左子树里，直径的右边在它的右子树里，而它的左右岔路的长度分别是它 左右子树的深度。

在当前拐弯的直径长度 = 左子树的最长链（深度）+ 右子树的最长链（深度）+ 2

而计算最长链也有明显的递归方程：

父节点为根节点的子树的最长链 = max（左子树的最长链，右子树的最长链）+ 1

由于每个点都遍历了一次，最差情况递归需要 $n$ 的栈空间：

• 时间复杂度为 $O(n)$
• 空间复杂度为 $O(n)$

代码

class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        ans = 0

        def dfs(node):
            if node is None:
                return -1 # 叶子节点链长为 0
            
            l_len = dfs(node.left)
            r_len = dfs(node.right)

            nonlocal ans
            ans = max(ans, l_len + r_len + 2)

            return max(l_len, r_len) + 1
        
        dfs(root)

        return ans