124. 二叉树中的最大路径和

题目

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

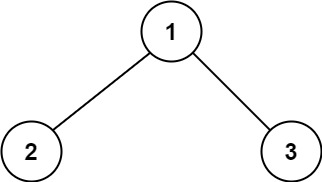
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

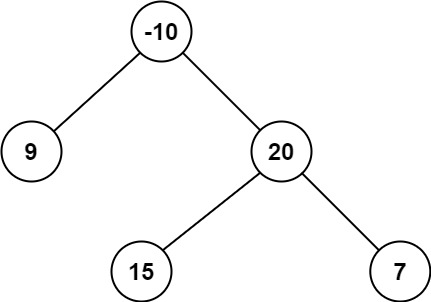
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

• 树中节点数目范围是 [1, 3 * 10^4]
• -1000 <= Node.val <= 1000

解答

思路

和 543 类似，仍然枚举拐弯点的位置，从枚举最大链长变成枚举 最大链和。

• 以拐点为根节点的 路径 的最大链和 = 左子树的最大链和 + 右子树的最大链和 + 当前节点值。
• 以拐点为根节点的子树中的最大链和 = max（左子树的最大链和，右子树的最大链和）+ 当前节点值。

注意：这里的节点值可能为负数，因此当碰到 最大链和小于零 的情况，可以直接剪枝掉这一棵子树。所谓路径并不一定是要 从叶子节点到叶子节点 的。

由于每个点都遍历了一次，最差情况递归需要 $n$ 的栈空间：

• 时间复杂度为 $O(n)$
• 空间复杂度为 $O(n)$

代码

class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        ans = -inf

        def dfs(node):
            if node is None:
                return 0
            
            l_sum = dfs(node.left)
            r_sum = dfs(node.right)

            nonlocal ans
            ans = max(ans, l_sum + r_sum + node.val)

            res = max(l_sum, r_sum) + node.val

            return res if res > 0 else 0 # max(max(l_sum, r_sum) + node.val, 0)
        
        dfs(root)

        return ans