17. 电话号码的字母组合

题目

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

• 0 <= digits.length <= 4
• digits[i] 是范围 ['2', '9'] 的一个数字。

解答

思路

如果要求构造一个长为 2 的字符串，其中第一个字符要在 abc 中选，第二个字符要在 def 中选，那么可以写一个二重循环来做。那如果要构造一个长为 5 的字符串呢？由此我们发现：单纯的 循环嵌套 表达能力是有限的（比如不能表达未知长度的字符串）。

• 原问题：构造长为 $n$ 的字符串
• 子问题：当我们枚举了第一个字母之后，就转为构造长为 $n-1$ 的字符串
• 将子问题的计算结果返回给原问题，既可以得到原问题的答案：适合使用递归来解决

回溯问题和递归有什么关系呢？回溯 往往有一个增量构造答案的过程，即在原计算结果的基础上再枚举一下就可以得到答案。

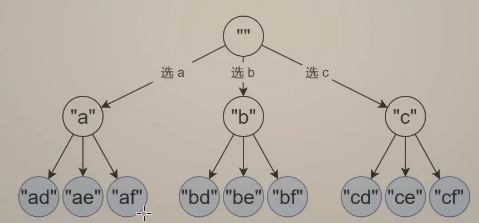
其实只要 边界条件 和 非边界条件 写对了，其他的事情交给数学归纳法即可。此时递归结果一定是正确的。我们需要把重点放在：如何从 选 a 切换到选 b 这个过程上面去。

我们用一个 path 数组记录路径上的字母。回溯三问：

• 当前操作是什么：枚举 path[i] 要填入的字母，这里引入了参数 i，因此是 dfs(i)
• 当前问题是什么：构造字符串 >= i 的部分
• 它的子问题是什么：已经枚举了一个字母，接下来是构造字符串 >= i + 1 的部分

注意需要做一个数字键盘到字母表的映射关系。

path 的每个位置最多有 $4$ 个不同的数，一共长度为 $n$，最后还需要一步把数组转化成字符串加入答案。而一般只算额外的空间复杂度，因此：

• 时间复杂度为 $O(n{4}^n)$
• 空间复杂度为 $O(n)$

代码

Python 代码

MAPPING = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"]

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        n = len(digits)

        if n == 0:
            return []
        
        ans = []
        path = [''] * n

        def dfs(i):
            if i == n:
                ans.append(''.join(path)) # 数组转化成字符串加入答案
                return
            
            for c in MAPPING[int(digits[i])]:
                path[i] = c  # 当前操作
                dfs(i + 1)   # 子问题
        
        dfs(0)

        return ans