102. 二叉树的层序遍历
题目
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
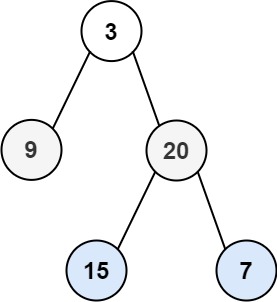
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]示例 2:
输入:root = [1]
输出:[[1]]示例 3:
输入:root = []
输出:[]提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
解答
思路:双数组替换
我们之前讲的递归也被称为 深度优先搜索 depth first search,DFS,而层序遍历则是一层一层的遍历。
- 初始化
cur数组,把根节点放入 - 遍历
cur数组,把当前数的左右儿子放到下一层节点数组nxt中去,得到 下一层节点 - 同时把节点值记录到
vals中 - 每当遍历结束,先将
vals加入答案数组中,再把cur替换为nxt开启下一轮循环
最后一层遍历完得到 nxt 是空的,为 cur 替换后也是空的,于是循环退出条件是 cur.size() == 0。
每个节点遍历一次,满二叉树情况下最后一层节点数目为 n/2,因此:
- 时间复杂度为
- 空间复杂度为
代码
C++ 代码
cpp
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (root == nullptr) {
return {};
}
vector<vector<int>> ans;
vector<TreeNode*> cur = {root};
while (cur.size()) {
vector<TreeNode*> nxt;
vector<int> vals;
for (auto& node : cur) {
vals.push_back(node->val);
if (node->left) {
nxt.push_back(node->left);
}
if (node->right) {
nxt.push_back(node->right);
}
}
ans.push_back(vals);
cur = nxt;
}
return ans;
}
};Python 代码
python
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
ans = []
cur = [root]
while cur:
nxt = []
vals = []
for node in cur:
vals.append(node.val)
if node.left:
nxt.append(node.left)
if node.right:
nxt.append(node.right)
cur = nxt
ans.append(vals)
return ans思路:队列
上一个代码中我们使用了两个数组 cur, nxt,我们试试能不能把它们拼接起来。当我们把下一层的节点加到末尾时,我们把当前层的节点去掉。这种 左出右进,也称为 先进先出 的数据结构叫做 队列 queue。当前层的所有节点出队后,队列中剩下的就恰好是下一层的所有节点。循环次数就是队列长度。
代码
Python 代码
python
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
ans = []
q = deque([root])
while q:
vals = []
for _ in range(len(q)):
node = q.popleft()
vals.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
ans.append(vals)
return ans层序遍历需要手写入队出队代码,和计算机自动维护的递归栈有所不同。