42. 接雨水
题目
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。示例 2:
输入:height = [4,2,0,3,2,5]
输出:9提示:
n == height.length1 <= n <= 2 * 10^40 <= height[i] <= 10^5
解答
思路
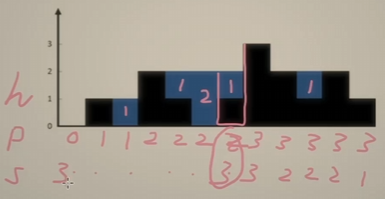
计算每个位置能接多少雨水:
- 左边高度是左边数组中的最大值,可以认为是左边有一个高的木板挡住了水
- 右边高度是右边数组中的最大值,同理
- 二者取较小值,就是当前 虚拟木板 的高度,减去 底座高度,得到结果
计算前缀最大值与后缀最大值:
- 前缀:从左到右取
max(nums[i], pre_max[i - 1]) - 后缀:从右到左取
max(nums[i], suf_max[i + 1])
由于需要两个额外的数组:
- 时间复杂度为
- 空间复杂度为
代码
C++ 代码
cpp
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
vector<int> pre_max(n);
vector<int> suf_max(n);
pre_max[0] = height[0];
for (int i = 1; i < n; i ++) {
pre_max[i] = max(pre_max[i - 1], height[i]);
}
suf_max[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; i --) {
suf_max[i] = max(suf_max[i + 1], height[i]);
}
int ans = 0;
for (int i = 0; i < n; i ++) {
ans += min(pre_max[i], suf_max[i]) - height[i];
}
return ans;
}
};Python 代码
python
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
pre_max = [0] * n
pre_max[0] = height[0]
for i in range(1, n):
pre_max[i] = max(pre_max[i - 1], height[i])
suf_max = [0] * n
suf_max[-1] = height[-1]
for i in range(n - 2, -1, -1):
suf_max[i] = max(suf_max[i + 1], height[i])
ans = 0
for h, pre, suf in zip(height, pre_max, suf_max):
ans += min(pre, suf) - h
return ans思路:空间优化
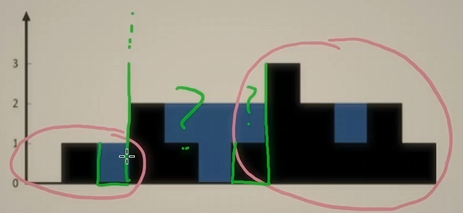
我们的时间复杂度已经是最优的了,接下来看能否优化空间。如图所示:图中红圈部分为已经确定前缀最大值和后缀最大值的部分。对于 height[2] 这个水块,虽然它右边的后缀最大值可能还会变大,但是前缀为 1 时已经确定的了,由于 height[2] 能盛多少水。
我们可以用两个指针分别指向左端点和右端点,同时用 pre_max, suf_max 记录前后缀的最大值:
- 初始值
pre_max = height[0], suf_max = height[n - 1] - 当
pre_max <= suf_max时,说明height[l]能盛多少水已经确定,因此l ++,更新pre_max = max(pre_max, height[l]) - 当
pre_max > suf_max时,说明height[r]能成多少水已经确定,因此r --,更新suf_max = max(suf_max, height[r]) - 二者相遇停止
由于没有额外空间:
- 时间复杂度为
- 空间复杂度为
代码
C++ 代码
cpp
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
int ans = 0;
int left = 0;
int right = n - 1;
int pre_max = height[left];
int suf_max = height[right];
while (left < right) {
if (pre_max <= suf_max) {
ans += pre_max - height[left];
left ++;
pre_max = max(pre_max, height[left]);
}
else {
ans += suf_max - height[right];
right --;
suf_max = max(suf_max, height[right]);
}
}
return ans;
}
};Python 代码
python
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
ans = 0
left = 0
right = n - 1
pre_max = 0
suf_max = 0
while left < right:
pre_max = max(pre_max, height[left])
suf_max = max(suf_max, height[right])
if pre_max < suf_max:
ans += pre_max - height[left]
left += 1
else:
ans += suf_max - height[right]
right -=1
return ans