区间动态规划
石子合并
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
cpp
4
1 3 5 2 -> 1 3 7 -> 4 7 -> 11
7 4 11 (22)显然不能用贪心来做。
- 状态表示:
f[i][j]去掉所有其他石子堆,只研究[i,j]区间内的石子堆,此时所有将第i堆石子到第j堆石子合并成一堆石子的合并方式(代价的最小值),而所求的最小值就是f[1][n] - 状态计算:合并一定存在最后一次合并,因此以最后一次合并所在的分界线位置来分类
- 分界线有
1 ~ n - 1共种,而对于 f[i][j]只有i ~ j - 1一共个 - 于是可以分为
类(或者可以这么分类:按照最后一次合并时左边已经合并了 [i,j]区间内的多少堆来分) - 一定要注意:
f[i][j]表示去除了其他的石子堆后的结果,因此任何一种合并方式最后一步的代价都是相同的,这里可以用前缀和来求解a[i]+...+a[j] = s[j] - s[i-1]; - 而剩下的
类合并则是 f[i][k] + f[k+1][j],其中。
- 分界线有
- 时间复杂度为
。
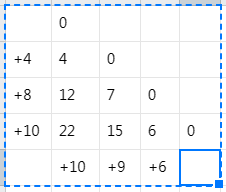
如上图所示,这是区间 DP 相较于线性 DP 的一大不同,打表方式这里是斜对角线依次打表,先算出 4, 7, 6,再算出 12, 15,最后算出答案 22。对于这种情况下的下三角矩阵,我们的循环代码为:
cpp
// normal
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= i; j ++) {
cin >> f[i][j];
}
}
// diagonal first
for (int t = 0; t < n; t ++) {
for (int i = 1; i <= n; i ++) {
cin >> f[i + t][i];
}
}它是先算:
cpp
f[1][1] f[2][2] f[3][3]
f[2][1] f[3][2]
f[3][1]体现的是 f[i][j] 中 j-i 的大小。因此也可以说这是以 长度 作为第一重循环变量,这也是区间 DP 的循环方式。
核心代码:
cpp
// ...
for (int len = 2; len <= n; len ++) {
for (int i = 1; i + len - 1 <= n; i ++) {
int l = i;
int r = i + len - 1;
f[l][r] = 1e9;
for (int k = l; k < r; k ++) {
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
}
}
}- 长度为 1 的
f[i][i]自然是 0,从长度为 2 开始计算 - 由于取的是最小值,因此先给
f[l][r]一个较大的数,之后会舍掉