前缀和与差分
前缀和
有一个长度为
- 如何求前缀和数组:递推公式,
,定义 - 前缀和数组的作用:快速求出原数组中 一段区间 的和,将时间复杂度从
变为
[l, r] 中的所有数的和,即 S[r] - S[l - 1]。
注意数组下标从 1 开始,为了定义 [1, 10] 就是 S[10] - S[0] = S[10]。将 前缀与区间和 合并成一类情况。
二维前缀和
快速求出某个子矩阵中所有元素的和。
定义二维前缀和数组
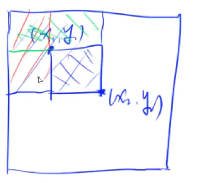
由图可知,所求阴影部分元素和为:
S[x2][y2] - S[x2][y1 - 1] - S[x1 - 1][y2] + S[x1 - 1][y1 - 1]
同理,计算二维前缀和数组也是类似的情况:
S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j]
差分
差分是前缀和的逆运算。
对于给定的 a[n] 数组,需要构造一个 b[n] 数组,使得 a[n] 是 b[n] 的前缀和。显然可以这么构造:
b[1] = a[1]b[2] = a[2] - a[1]b[i] = a[i] - a[i - 1]
b[n] 数组就称为 a[n] 数组的差分,a[n] 数组称为 b[n] 数组的前缀和。
如果我们有了 b[n] 数组,可以在 a[n] 数组。
差分数组主要用来解决以下这一类问题:现在有大量如下操作,需要对 a[n] 数组的不同区间 [l, r] 同时加上不同的数 c[i],询问返回的新数组。
差分数组可以在 a[n] 数组。相较于原先的
假如区间 [l, r] 同时加上数 c,那么:
b[l] = b[l] + c,表示a[l] += c,但是a[l - 1]不变b[r + 1] = b[r + 1] - c,表示a[r] += c,但是a[r + 1]不变- 中间不发生变化,说明
a[l, r]中间的任意相邻两个数之间的差不变
那么如何构造 b[n] 数组呢?我们可以假设 a[n] 数组初始的时候为 0,之后是看作进行了 n 次插入操作,将 [i, i] 区间加上 a[i]。
b[1] = 0 + a[1]b[2] = 0 - a[1] + a[2]b[i] = 0 - a[i - 1] + a[i]
差分矩阵
需要满足原矩阵 a[i][j] 是差分矩阵 b[i][j] 的前缀和矩阵。
一样的,也不考虑如何构造,而是考虑如何更新。二维差分要解决的问题就是给 a[i][j] 中的某个子矩阵加上一个特定的值 c。
考虑 b[i][j] += c; 对应的前缀和矩阵 a[i][j] 中的效果,是将 += c。因此:
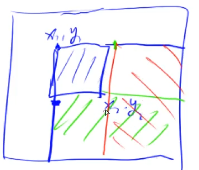
b[x1][y1] += c;将右下角的一片都 += cb[x2 + 1][y1] -= c;将右下角的一片都 -= cb[x1][y2 + 1] -= c;将右下角的一片都 -= cb[x2 + 1][y2 + 1] += c;将右下角的一片都 += c
因此将
也可以认为是先对全零矩阵做操作,然后再将 a[i][j] 做插入操作,利用了加法的交换不变性。