BFS

宽度优先搜索 Breadth First Search，BFS。也称为广度优先搜索。从根节点出发后，优先从离起点更近的顶点开始搜索，可以看作是每一层每一层进行搜索。

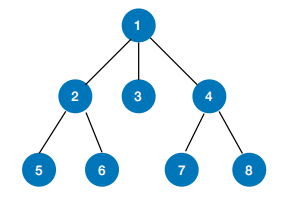
如图所示，从 1 开始的 BFS 结果为：

cpp

1 2 3 4 5 6 7 8

BFS 使用 优先级队列 来实现，因为它对于每个点都需要判断 它和起点之间的距离，从而看是否将其加入搜索队列。BFS 每次会把整个一层的节点（距离相同的节点）存储下来，因此树的 BFS 需要空间为 $O (2^{h}) = O (n)$ 。

由于 BFS 优先从离起点近的点开始搜索，因此 BFS 搜索到的路径具有 最短路 的性质。

八数码

cpp

1 2 3      1 2 3
x 4 6  ->  4 5 6
7 5 8      7 8 x

求的是最小步数。

把每个 状态看作是图中的一个节点。如果状态能够互相转移，则连一条边。找到起始状态和终点状态之间边的个数。

难点就在于：

状态表示比较复杂，每一个状态是 3*3 的矩阵（字符串？）
如何把状态放到 BFS 的队列中
如何定义 dist 数组，也就是每个状态的距离（两个信息，状态 & 距离）
状态转移该怎么做？（上下左右四个方向）
- 首先将字符串转译成矩阵
- 矩阵进行操作，上下左右移动
- 最后将结果矩阵转译成字符串存储

AC845. 八数码

对于字符串 "1234x5678" 需要熟练掌握一维转二维的坐标变换：

cpp

// 1d to 2d
int x = k / 3;
int y = k % 3;

// 2d to 1d
int k = 3*x + y;

在上下左右完成状态转移之后，记得要恢复现场：

cpp

// ...
for (int i = 0; i < 4; i ++) {
    int nx = x + dx[i];
    int ny = y + dy[i];

    if (nx >= 0 && nx < 3 && ny >= 0 && ny < 3) {
        swap(t[k], t[3*nx + ny]);  // 更新新的状态

        if (!d.count(t)) {
            d[t] = distance + 1;
            q.push(t);
        }

        swap(t[k], t[3*nx + ny]);  // 恢复现场
    }
}

BFS ​

八数码 ​

BFS

八数码