堆

使用数组模拟堆，C++ 中就是 priority_queue，默认是大顶堆，堆需要满足的操作：

向堆中插入一个元素
求堆中的最小值
删除最小值
删除任意一个元素（数组支持，STL 不支持）
修改任意一个元素（数组支持，STL 不支持）

堆的基本结构是一棵 完全二叉树，除了最后一层节点之外，上面所有节点都是满的，最后一层节点按照从左到右排列。小根堆满足：根节点元素的值 小于等于左右儿子，因此整个堆的根节点是全堆的最小值。

首先我们要用一个一维数组来存储这一棵完全二叉树：

a[1] 为根节点
a[x] 的左儿子为 a[2 * x]
a[x] 的右儿子为 a[2 * x + 1]（数学归纳法易证）

堆的两个操作函数：

down(x)：往下调整
up(x)：往上调整
以上五个操作可以用这两个操作函数组合实现

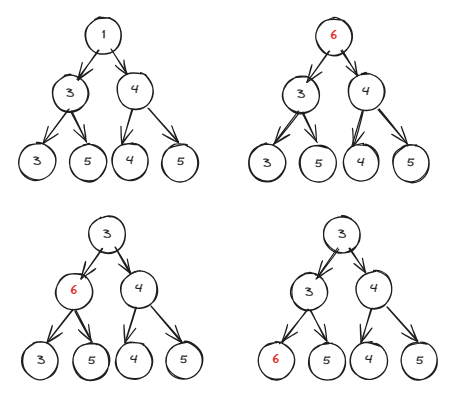
down(x) 操作如图所示，当根节点变大后：

比较它的左右儿子，选择其中的较小者，二者交换
重复上述操作，直到根节点比左右儿子小或者到达叶子节点时结束
down(x) 操作主要针对插入元素数值变大的情况

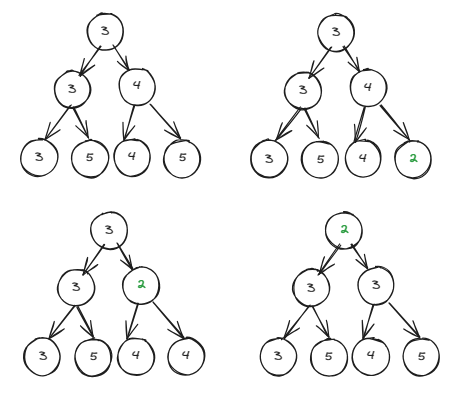
up(x) 操作如图所示，当某个节点变小后：

和它的根节点对比，如果比根节点小，则与根节点交换
注意：根节点交换下来后，一定比它新的左右儿子小（因为每一层都比下一层小）
重复上述操作，直到到达顶点或者大于根节点时结束
up(x) 操作主要针对堆中元素数值变小的情况

五个操作分解：

插入操作：
- 尾部插入：heap[++ size] = x;
- 不断将其往上移动：up(size)
查询最小值：
- 返回堆顶元素：heap[1]
删除最小值：
- 把最后一个元素 t 覆盖到堆顶（此时最小值相当于已经被删除）heap[1] = heap[size];
- size --; 删除最后一个元素
- 不断将堆顶元素下移：down(1);
- 这是因为数组删除头元素很困难
删除任意一个元素：
- heap[k] = heap[size], size --;
- 可能会有变大变小两种情况，直接 up(k), down(k) 都来一遍即可
- 上面只会执行一次
修改任意一个元素：
- heap[k] = x, down(k), up(x);
注意到，up(k), down(k) 这两个操作中的参数都是下标 $k$

堆排序

需要用到的操作：

建堆
删除元素
注意到只会使用 down() 操作，它和 up() 操作的时间复杂度都与堆的高度成正比， $O (\log n)$
- 如果采用一个一个插入的方式建堆，时间复杂度就已经是 $O (n \log n)$ 了
- 而我们只需要从下标 n/2 位置开始，依次做 down 操作到 1 即可，时间是 $O (n)$ 的

下标为 n 的位置是堆的最后一个数，也在最后一层，因此 n/2 的数在倒数第二层
它的 down() 操作时间复杂度为 $O (1)$ ，本层一共有 n/4 个点
同理，倒数第三层有 n/8 个点，down() 操作时间复杂度为 $O (2 \times n / 8)$
同理，倒数第四层有 n/16 个点，down() 操作时间复杂度为 $O (3 \times n / 16)$
等等

综上可知：总的时间复杂度为：

\frac{n}{4} \times 1 + \frac{n}{8} \times 2 + \frac{n}{16} \times 3 + \dots + 1 \times \log n

这是一个等差乘等比数列：

\begin{aligned} S & = \frac{1}{2^{2}} \times 1 + \frac{1}{2^{3}} \times 2 + \frac{1}{2^{4}} \times 3 + \dots \\ 2 S & = \frac{1}{2} \times 1 + \frac{1}{2^{2}} \times 2 + \frac{1}{2^{3}} \times 3 + \dots \\ 2 S - S & = \frac{1}{2} \times 1 + \frac{1}{2^{2}} \times 1 + \frac{1}{2^{3}} \times 1 + \dots < 1 \end{aligned}

因此总的时间复杂度就是 $O (n)$ 。

为什么从下标 n/2 位置开始 down 就能得到一个正确的堆呢？可以这么理解，就算把所有数都 down 一遍，事实上进行了 down 操作的也只有下标 n/2 位置开始的数，其他数都是叶子节点，不会进行 down 操作。

AC838. 堆排序

down 函数核心代码：

cpp

void down(int k) {
    int t = k;
    
    if (k * 2 <= size && h[k * 2] < h[t]) {
        t = k * 2;
    }
    if (k * 2 + 1 <= size && h[k * 2 + 1] < h[t]) {
        t = k * 2 + 1;
    }

    if (k != t) {
        swap(h[k], h[t]);
        
        down(t);
    }
}

up 函数核心代码：

cpp

void up(int k) {
    while (k / 2 >= 1 && h[k / 2] > h[k]) {
        swap(h[k / 2], h[k]);

        k /= 2;
    }
}

甚至比 down 还要简单。

可以直观理解一下：一个 1,000,000 节点的堆也不过 20 层。

模拟堆

AC839. 模拟堆

由于不使用哈希表，因此加入两个额外数组：

ph[j] = k：表示第 $j$ 个插入的数在 heap 中的下标为 $k$
hp[k] = j：表示在 heap 中下标为 $k$ 的数是第 $j$ 个插入的数

核心交换代码：

cpp

void heap_swap(int i, int j) {
    int k1 = hp[i];
    int k2 = hp[j];
    swap(ph[k1], ph[k2]); // swap ph

    swap(h[i], h[j]);     // swap heap 

    swap(hp[i], hp[j]);   // swap hp
}

想要交换 heap 中下标为 i, j 的两个元素
首先找到它们分别是第 k1, k2 个插入的元素
交换 heap 数组，原先下标为 i 的变成 j，下标为 j 的变成 i
交换 ph[] 数组，此时第 k1 个插入的元素变成了 heap[j]，也就是下标为 j 的元素
交换 hp[] 数组，下标为 j 的元素此时在 ph[] 数组中，需要用 k1 来进行索引

堆 ​

堆排序 ​

模拟堆 ​

堆

堆排序

模拟堆