匈牙利算法

匈牙利算法可以求二分图的最大匹配。

最坏情况下： $O (n m)$
一般实际情况下运行时间远小于最坏情况（这种情况常见于 最大流算法）

图的匹配定义：图中匹配是指这个图的一个 边的集合，集合中任意两条边都没有公共的顶点，则称这个边集为一个匹配。我们称匹配中的边为匹配边，边中的点为匹配点；未在匹配中的边为非匹配边，边中的点为未匹配点。

最大匹配：一个图中所有匹配中，所含 匹配边数最大 的匹配称为最大匹配。
完美匹配：如果一个图的某个匹配中，图的所有顶点都是匹配点，称为完美匹配
显然，完美匹配一定是最大匹配，不是所有图都存在完美匹配

如图所示：

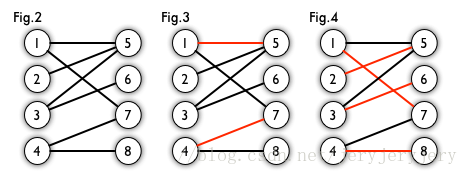
1701421910175

Fig.2 是某个二分图
Fig.3 是该二分图的一个匹配
Fig.4 是该二分图的一个最大匹配，同时也是完美匹配

匈牙利算法流程：

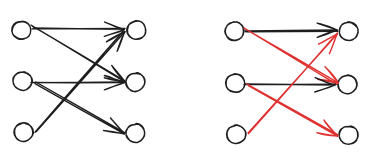
根据增广路的思想，以一个未匹配的节点出发，遍历图，不断的寻找增广路来扩充匹配的边数，直到不能扩充为止。

比如左侧的 1 号点，原先匹配右侧的 1 号点（同时它也能匹配右侧的 2 号点）
此时左侧的 2 号点，可以匹配右侧的 2 号点（同时它也能匹配右侧的 3 号点）
然而左侧的 3 号点，只能匹配右侧的 1 号点
- 此时回溯寻找左侧 1 号点有无其他可匹配点，发现 2 号点
- 但此时 2 号点被占，依然回溯去看占有其的左侧 2 号点有无其他可匹配点
- 直到无法匹配或者匹配成功为止

时间复杂度： $O (n m)$ ， $n$ 为左侧点个数， $m$ 为所有边数。

AC861. 二分图的最大匹配

核心代码：

cpp

bool find(int x) {
    for (int i = h[x]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {
            st[j] = true;

            if (match[j] == 0 || find(match[j])) {
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}

对每个点 x，依次寻找邻接表上相连的右侧点 j
二话不说先把 j 占了，然后回头看 match[j] 是否有主
- 没有，直接宣布主权 match[j] = x;，返回匹配成功
- 有，只能让上家重新找右侧的匹配点
- 注意此时在 if 判断中，只有上家找到了无冲突的点，才能进入作用域中
这里的 st[j] 每一层递归只会将一个变为 true，它保证之后的递归中无法被使用

需要理解这个递归函数 find()，它表示 找到一个和之前都不冲突的匹配点。也就是说 match[j] < x。

以及这一段：

cpp

// ...
    for (int i = 1; i <= n1; i ++) {
        memset(st, 0, sizeof st);

        if (find(i)) {
            res ++;
        }
    }

对于每个左侧的点，在找它的匹配点之前需要将上一个点的 st 数组清空

匈牙利算法 ​

匈牙利算法