KMP

KMP 算法用于字符串匹配。

给定一个字符串 S，以及一个模式串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。模式串 P 在字符串 S 中多次作为子串出现。求出模式串 P 在字符串 S 中所有出现的位置的起始下标。

首先思考暴力做法：

cpp

for (int i = 1; i <= n - m; i ++) {
    int j = 1;
    
    while (j <= m) {
        if (s[i + j] != p[j]) {
            break;
        }
        j ++;
    }

    if (j == m + 1) {
        return i;
    }

    return -1;
}

循环字符串 S 的起点 s[i]，以及模式串 P 的起点 p[j]
按照模式串长度挨个匹配 s[i + j] ?= p[j]
- 不匹配，跳过这次循环 i ++
- 匹配，继续匹配 P 中的下个字符，j ++
直到模式串的最后一个字符匹配完成，此时 j == m + 1，返回字符串 S 的起点 i

我们回顾一下匹配的过程：当我们匹配失败的时候，如图所示，在绿色和红色圈圈的位置匹配失败：

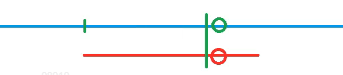
此时暴力做法是将红色的模式串往后移动一位，我们认为这样做太慢了，因为我们前面已经匹配了很长的一段，一定保留了一些信息。于是我们就思考，如果不仅仅移动一位，那么需要将红色的模式串往后移动多少位呢？

假设移动了 $k$ 位，那么说明模式串的前缀 p[0~k] 一定和模式串中间的一段相同才行
模式串向右移动的长度越少，说明前缀串内匹配的长度越长
如果前缀在串内都没有匹配，例如 "abcdef" 中的任意前缀都没有串内匹配，那么可以飞速跳跃
于是我们可以知道，循环节越少的模式串匹配起来越快

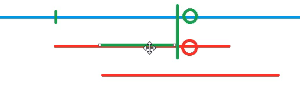
因此我们需要对模式串 P 的每一位 p[k] 预处理 以它为终点的后缀 和前缀有多少匹配，也就是 p[0~i] == p[k-i,k] 的最大的 i 是多少。当然满足上述式子的 i 可能不止一个，但是最大的 i 才能保证最小的右移幅度。我们用 next[k] 记录这样的 i。

因此我们的流程变为：

每当发现 s[i] != p[j] 时
找到 p[j - 1] 对应的 next[j - 1] = k
将模式串右移，继续比较 s[i] 和 p[k + 1]
- 因为此时 p[0, k] == p[j-k-1, j-1]

一般而言，我们为了简化，可以让 S 和 P 下标都从 1 开始，p[0] = * 认为是一个通配符，这样做的好处是，当 "abcdef" 这种模式串出现时，那么它的所有 next[i] 均为 0。

每次比较 s[i] 和 p[j + 1]
- 相等，则 i ++, j ++（注意 i ++ 是外层大循环）
- 不等，跳跃：j = next[j]，继续比较（写作一个 while 循环）
由于 j 一直向左跳跃，因此可能会到 0，此时说明没有前缀与以 p[j] 结尾的后缀相同
- 也说明 s[i] 前面的所有字符串和 P 都无法匹配
- i ++, j = 0，重新比较 s[i + 1] 和 p[1]

cpp

// ...
    // KMP match
    for (int i = 1, j = 0; i <= m; i ++) {
        while (j > 0 && s[i] != p[j + 1]) {
            j = ne[j];
        }

        if (s[i] == p[j + 1]) {
            j ++;
        }

        if (j == n) {
            // success

        }
    }

这里有另一种解释：

每次比较 s[i] 和 p[j + 1]
一旦发现不等，进入 while 循环，循环是 j = next[j]，注意循环退出条件
- s[j] == p[j + 1]，此时循环退出
- j = 0 说明无前缀匹配，循环退出
循环退出后由于有两种情况，需要判断一下 s[i] ?= p[j + 1]
- 例如 s[i] == p[1] 这种特殊情况
- 二者相等，说明匹配成功，i ++, j ++
- 二者不等，说明 s[i] 以及它之前的字符串都无法和 P 匹配，i ++
最后判断 j ?= n，相等说明匹配成功

那么如何求出模式串 P 的 next 串呢？

next[1] = 0
i = 2 开始循环，每次判断 p[i] ?= p[j + 1]，也就是将 p[1~i] 当作 S 串重写上述操作
由于每次向右移动的幅度是最小的，因此当循环中 p[i] == p[j + 1] 时，前缀最长，记录 next 数组
- 由此可以理解为暴力算法的 next 数组满足 next[i] = i - 1;
当下一位直接 p[i] == p[j + 1] 时，由反证法可知此时的 next[i] = j
- 如若不然，那么有更长的前缀，与 next[i - 1] = j - 1 的结论矛盾

核心代码：

cpp

// ...
    // KMP next
    for (int i = 2, j = 0; i <= n; i ++) {
        while (j > 0 && p[i] != p[j + 1]) {
            j = ne[j];
        }

        if (p[i] == p[j + 1]) {
            j ++;
        }

        ne[i] = j;
    }

似乎这么写更好理解？但是太不美观，注意合并 if 和 while。

cpp

for (int i = 2, j = 0; i <= n; i ++) {
    if (p[i] != p[j + 1]) {
        while (j > 0 && p[i] != p[j + 1]) {
            j = ne[j];
        }
    }

    if (p[i] == p[j + 1]) {
        j ++;
    }

    ne[i] = j;
}

AC831. KMP 字符串

最后来手动算一个 next 数组：

cpp

P = "ababaaab"

next[1] = 0;
next[2] = 0;
next[3] = 1;
next[4] = 2;
next[5] = 3;
next[6] = 1;
next[7] = 1;
next[8] = 2;

在计算 next[6] 的时候，j = next[5] = 3 不行，j = next[3] = 1 还是不行，最后 j = next[1] = 0，然后又发现此时 p[i] == p[j + 1]，因此 next[6] = 1。

j ++ 就是在增长匹配前缀的长度，使得向右移动幅度最小。

这个例子也很有意思：

cpp

P = "aaaa"

next[1] = 0;
next[2] = 1;
next[3] = 2;
next[4] = 3;

思考 KMP 算法的时间复杂度：

i 循环 $m$ 次，j 最多 ++ $m$ 次
while 循环最多 -- $m$ 次
时间复杂度为 $O (2 m)$

KMP ​

KMP