Trie
Trie 树也被称为字典树。可以用来高效地 存储和查找 字符串集合。
例子:
cpp
abcdef
abdef
aced
bcdfTrie 树一般要求字符集合的元素个数不是很多(全是小写字母、全是大写字母、全是数字等等)它可以存储上述的数据:
- 从根节点开始,对于
"abcdef"首先观察根节点有没有"a"节点,没有就创建- 再找
"a"节点有没有"b"节点 - 以此类推
- 再找
- 再看第二个单词,此时根节点有
"a"子节点,因此不用创建,接着往下走- 直到走到
"b",发现它没有"d"节点,因此创建
- 直到走到
- 重复上述操作,直到遍历所有字符串
- 注意:当我们插入完成后,在结束位置打一个标记
Trie 树大致样子:
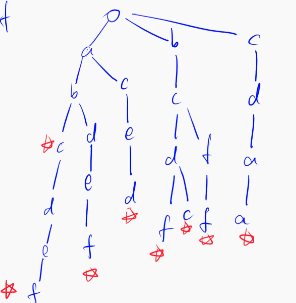
Trie 树除了存储之外,还能快速查找,注意当我们字符匹配后,还需要看结尾有没有标记,这样才能判断 Trie 树中是否有该字符串。没有路径或者结束时没有标记都算作没有这个字符串。
核心代码:
cpp
void insert(char str[]) {
int p = 0;
for (int i = 0; str[i] != '\0'; i ++) {
int u = str[i] - 'a';
if (son[p][u] == 0) {
idx ++;
son[p][u] = idx;
}
p = son[p][u];
}
cnt[p] ++;
}其中:
son[p][u]的值为p节点的子节点编号,u表示p节点对应的字符串- 感觉可以用结构体数组来写?
node[k]的子节点和本节点存储的字符
- 初始值为 0,表示子节点为空
- 最后在结束下标的位置上打一个标记,
cnt[p] ++;
cpp
struct Node {
int son;
char c;
} node[N];查找代码:
cpp
int query(char str[]) {
int p = 0;
for (int i = 0; str[i] != '\0'; i ++) {
int u = str[i] - 'a';
if (son[p][u] == 0) {
return 0;
}
p = son[p][u];
}
return cnt[p];
}最大异或对
在给定的
思考暴力做法:二重循环来做
cpp
int res = 0;
for (int i = 0; i < n; i ++) {
for (int j = 0; j < n; j ++) {
res = max(a[i] ^ a[j], res);
}
}思考,在给定 a = 11001100....0011 这种。对于它,我们从高位到低位思考:
- 第 31 位一定是为 0 的比为 1 的异或结果大,因此进入第 31 位为 0 的数分支
- 第 30 位一定是为 0 的比为 1 的异或结果大,因此进入第 30 位为 0 的数分支
- 第 29 位一定是为 1 的比为 0 的异或结果大,因此进入第 29 位为 1 的数分支
- 重复上述操作,如果某一位只有一个分支,直接进入即可
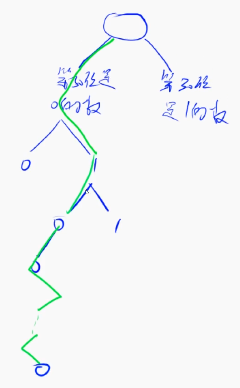
长得很像 Trie 树,因此可以用 Trie 树存储。在使用 Trie 树之后,只需要走 31 步就能找到
Trie 树的节点个数为 t[3100010][2]。