拓扑排序
有向图的 拓扑序列 就是图的 BFS 的一个应用。拓扑序列一定是针对有向图而言的。
若一个由图中所有点构成的序列
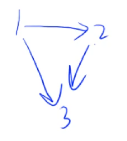
如图所示,1 2 3 就是一个拓扑序列,对于每一条边而言:
cpp
1 2 3
1 -> 2
2 -> 3
1 -> 3起点相较于终点都在拓扑序列的前面。当我们按照拓扑序排列好之后,所有的边都是从前指向后的。
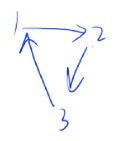
- 并不是所有的有向图都有拓扑序
- 显然存在环的图一定不存在拓扑序
- 可以证明:有向无环图一定存在拓扑序列
有向无环图 Directed Acyclic Graph,DAG 也被称为拓扑图。
入度和出度的介绍:
- 入度:一个点有多少条边指向自己(以它为终点)
- 出度:一个点有多少条边出发(以它为起点)
对于一个拓扑序列来说,由于所有的边都是从前指向后的,因此任何一个 入度为 0 的点都可以作为拓扑序列的起点(或者说靠前的位置)。显然,DAG 一定至少存在一个入度为 0 的点,否则以任意点出发找它上一个点,最终一定可以得到一个环(抽屉原理),这与 DAG 矛盾。
求拓扑序列的算法:
- 把所有入度为 0 的点入队
- 从队头取出一个节点
t- 枚举
t的所有出边t -> j - 删除这条边,因为
t此时已经放置于拓扑序列前端,t -> j一定是从前指向后的 j的入度将会 -1:d[j] --;- 如果此时
j的入度为 0,说明j的所有前驱已经在拓扑序列中,将j入队
- 枚举
- 因此对于一个没有环的图,一定可以按照这个算法获得一个拓扑序列
核心代码:
cpp
bool topsort() {
int hh = 0, tt = -1;
for (int i = 1; i <= n; i ++) {
if (d[i] == 0) {
q[++ tt] = i;
}
}
while (hh <= tt) {
int t = q[hh ++];
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
d[j] --;
if (d[j] == 0) {
q[++ tt] = j;
}
}
}
return tt == n - 1;
}