Ereshki's Blog

Appearance

线性动态规划 ​

什么是线性 DP？指的是我们的 递推方程是线性的，例如之前的背包问题。由于递推方程是线性的，因此线性 DP 的状态求解顺序也是线性的，可以从左到右，从上到下依次求解。

数字三角形 ​

数字三角形堪称 DP 第一题。

由于只能朝左下方或者右下方，因此调整成直角三角形，要求只能朝正下方或者右下方即可：

cpp
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5
  • 状态表示：f[i][j] 表示以 (i,j) 坐标为终点的路径上和的最大值
  • 状态计算：它只能由左上方或正上方转移过来
  • 即 f[i][j] = max(f[i-1][j-1], f[i-1][j]) + a[i][j]
  • 初始化：给外部包裹一层 -INF，这样递推的时候更方便

核心代码：

cpp
// ...
    for (int i = 1; i <= n; i ++) {
        f[i][0] = -INF;
        f[i][i + 1] = -INF;
    }

    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= i; j ++) {
            f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
        }
        
    }
  • 注意这里不仅要让 f[i][0] 为 -INF
  • 由于 f[i][i] 会用到 f[i-1][i]，因此 f[i][i+1] 也都要设置为 -INF
  • 既然如此，直接把整个 f[][] 设置为 -INF 不就好了，时间复杂度也没有增加
  • 最后考虑最后一行中的 max，因此可以设置 res 的初始值也为 -INF
cpp
// ...
    for (int i = 0; i <= n; i ++) {
        for (int j = 0; j <= n; j ++) {
            f[i][j] = -INF;
        }
    }
    f[1][1] = a[1][1];

    for (int i = 2; i <= n; i ++) {
        for (int j = 1; j <= i; j ++) {
            f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
        }
    }

这样就需要设置初始值 f[1][1] = a[1][1];，以及从第二行开始求。

AC898. 数字三角形

DP 的时间复杂度：状态数量 * 转移计算时间复杂度，本题为 O(n2)。

一维优化：记得倒序

cpp
// ...
    for (int i = 0; i <= n; i ++) {
        f[i] = -INF;
    }
    f[1] = 0;

    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= i; j ++) {
            cin >> a[j];
        }

        for (int j = i; j > 0; j --) {
            f[j] = max(f[j], f[j - 1]) + a[j];
        }
    }

最长上升子序列 I ​

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

cpp
3 1 2 1 8 5 6
->
1 2 5 6
  • 状态表示：f[i] 表示以 a[i] 结尾的上升子序列集合（长度的最大值）
  • 状态计算：
    • 显然，可以分 i 类，分别为 a[0]...a[i-1] 结尾的上升子序列集合
    • 保证单调递增，因此需要 a[j] < a[i]
    • 要求长度的最大值，因此是 max(f[j] + 1)
  • 初始化：f[0] = 1

状态数量为 n，每个状态需要考虑的转移方程个数也为 n，因此时间复杂度为 O(n2)。

核心代码：

cpp
// ...
    for (int i = 0; i < n; i ++) {
        f[i] = 1;

        for (int j = 0; j < i; j ++) {
            if (a[j] < a[i]) {
                f[i] = max(f[i], f[j] + 1);
            }
        }
    }

AC895. 最长上升子序列

还可以用一个 g[] 数组存储转移过程下标：

cpp
for (int j = 0; j < i; j ++) {
    if (a[j] < a[i]) {
        if (f[i] < f[j] + 1) {
            f[i] = f[j] + 1;

            g[i] = j;
        }
    }
}

// ...
for (int i = 0, len = f[k]; i < len; i ++) {
    cout << a[k] << " ";
    k = g[k];
}

最长公共子序列 ​

给定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。

  • 状态表示：f[i][j] 表示所有由第一个序列前 i 个字母和第二个序列前 j 个字母中的公共子序列（长度的最大值）
  • 状态计算：分为四种子结构
    • 不选 a[i]，不选 b[j]：f[i-1][j-1] 不如第四种情况，可以舍去
    • 不选 a[i]，选 b[j]：f[i-1][j] 包含这种情况
    • 选 a[i]，不选 b[j]：f[i][j-1] 包含这种情况
    • 选 a[i]，选 b[j]：f[i-1][j-1] + 1
  • 我们注意到这四种子结构可能会互相包含（例如 f[i-1][j] 一定包含了 f[i-1][j-1]），但是一定不会漏掉。而我们要求的是最大值，因此即使互相包含了，只需要分别求出最大值，再取最大值即可。

AC897. 最长公共子序列

核心代码：

cpp
// ...
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]);

            if (a[i] == b[j]) {
                f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
            }
        }
    }

注意读取的时候需要从字符串的第 1 位而不是第 0 位开始读取，为 f[i-1][j-1] 留出空间。

如果我们用的是 int a[N];，然后用 scanf("%s", a + 1); 读入，也就是把 abcd 放到了整型数组的第二位上，因此 a[1] = 0x61626364。

最长上升子序列 II ​

上一道题的时间复杂度是 O(n2)。这里 N=105 会超时。

回顾一下之前的做法：

  • 对于以 a[i] 结尾的数，根据它倒数第二个数分为 i 类
  • 只要满足 a[k] < a[i]，就将其考虑进入，f[i] = max(f[k] + 1);

思考一下求的过程中有没有冗余？考虑这样的序列 1 3 1 2 5：

  • 对于 5 而言，1 3 和 1 2 都是长度为 2 的序列，但是 3 比 2 更大
  • 因此对于这之后的数，想要扩展为长度为 3 的上升子序列，则只需要选择 1 2 序列即可
  • 因此我们可以对于 a[i] 之前的所有序列按照长度分类，然后只存储每一类中最小的那个序列即可（存储结尾值）
  • 例如对于 5 而言，长度为 1, 2, 3 的单调上升序列结尾值是 1, 2, 5

所以结尾值是否一定是随着长度上升而 单调递增 的呢？

显然，如果长度为 4 的结尾值比长度为 3 的结尾值要小的话（或者等于），说明该长度为 4 的序列倒数第二个数比长度为 3 的结尾值也要小，而这与我们仅存储同等长度序列中 结尾值最小 的相矛盾。

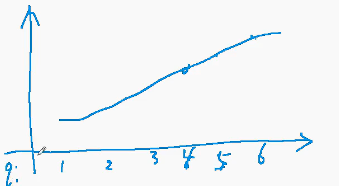
image-20231206145200233

  • 横坐标为最长上升子序列的长度
  • 纵坐标为结尾值最小的那个结尾值（对于长度为 1 的序列，结尾值在 a[0->n-1] 的过程中它是不断降低的）
  • 我们要找以 a[i] 结尾的最长上升子序列，就是找到纵坐标小于 a[i] 的横坐标（二分问题）

考虑时间复杂度：

  • 每次更新是 O(log⁡n) 的，二分查找到 a[i] 应该在哪个结尾值 q[j] 的后面
  • 然后比较 q[j + 1] 和 a[i] 大小，如果 a[i] 更小就替换
  • 一共循环 n 次，所以时间复杂度为 O(nlog⁡n)

AC896. 最长上升子序列 II

最短编辑距离 ​

  • 状态表示：
    • 集合：所有将 A[1~i] 变为 B[1~j] 的操作方式
    • 属性：操作次数最小值 f[i][j]
  • 状态计算：
    • 删除：需要使得 A[1~i-1] 已经和 B[1~j] 匹配了，f[i-1][j] + 1
    • 增加：需要使得 A[1~i] 已经和 B[1~j-1] 匹配了，f[i][j-1] + 1
    • 修改，需要使得 A[1~i-1] 已经和 B[1~j-1] 匹配了，这里需要判断 A[i] ?= B[j]，所以是 f[i-1][j-1] + 0 或者 f[i-1][j-1] + 1
    • 以上三种子状态取最小值
  • 时间复杂度 O(3n2)

这里有人会问了？凭什么 f[i][j] 一定只从这三个状态转移过来呢？比如我 ABCDA -> ABEDA 明明就是中间 D -> E 这一步啊，看上去并不是从 [ABCD, ACEDA], [ABCDA, ACED], [ABCD, ABED] 这三种状态通过增加删除修改操作转移过来的啊？

这时候我们就要画一幅状态转移图：

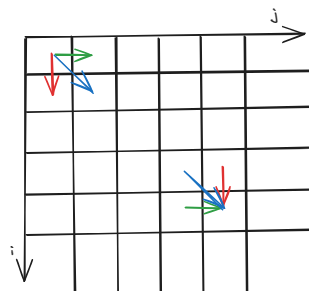
image-20231206153757204

  • 红色代表删除：f[i-1][j] + 1，每次转移 +1
  • 绿色代表增加：f[i][j-1] + 1，每次转移 +1
  • 蓝色代表修改：f[i-1][j-1] + 1, f[i-1][j-1] + 0，每次转移可以 +0

f 矩阵为：

cpp
0 1 2 3 4
1 0 1 2 3
2 1 1 2 3
3 2 2 1 2
4 3 3 2 1

可以看出沿着对角线下来的是最快的。而且它确实是由 [ABCD, ABED] 经过 0 步转移得到的。

AC902. 最短编辑距离

核心代码：

cpp
// ...
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);

            if (a[i] == b[j]) {
                f[i][j] = min(f[i][j], f[i - 1][j - 1]);
            }
            else {
                f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
            }
        }
    }

注意边界：

cpp
// ...
    for (int i = 0; i <= m; i ++) {
        f[0][i] = i;
    }
    for (int i = 0; i <= n; i ++) {
        f[i][0] = i;
    }

编辑距离 ​

求每个字符串与给定字符串的编辑距离，判断是否小于给定操作次数即可。

AC899. 编辑距离

Released under the MIT License.

Copyright © 2024-present Ereshki