DFS
深度优先搜索 Depth First Search,DFS。每次会尽量往深处搜索,直到叶节点处进行回溯(回溯指的是返回上一层节点,再查看当前节点有无 没有搜索过的子节点。
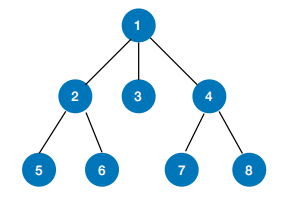
如图所示,从 1 开始的 DFS 结果为:
cpp
1 2 5 6 3 4 7 8DFS 使用栈(递归函数栈)实现,由于 DFS 需要记录路径上的点(方便回溯),因此 DFS 需要使用的空间与树的高度成正比
排列数字
DFS 的搜索流程是一棵树。
如何思考 排列数字?正常来说人类都是划出 3 个空格,然后挨个填入数字,注意,下一个填入的数字要求前面从来没有出现过。
path[N]:结果数组,占位空格st[N]:当我们for循环遍历数字的时候,用来表示前面是否用过该数字- 回溯需要 恢复现场
核心代码:
cpp
// ...
for (int i = 1; i <= n; i ++) {
if (!st[i]) {
path[u] = i;
st[i] = true;
dfs(u + 1); // 这一步结束就是回溯到上一层节点
st[i] = false;
}
}注意到,这里的搜索顺序就是 空格。
八皇后
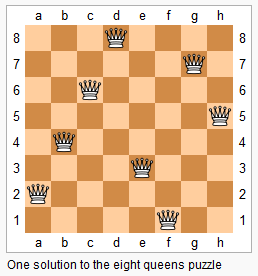
首先思考搜索顺序。
- 64 格子,一个格子一个格子进行搜索
- 8 行,由于皇后可以攻击一整行,所以一行一行搜索,看这一行的皇后放在哪一列
- 这么一看,如果对角线不能攻击的话,似乎就是一个全排列问题
因此这里还需要边做边判断是否相互攻击,攻击了就剪枝掉(有点类似 st[N])。
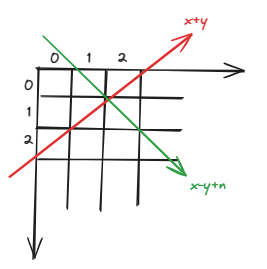
- 对角线是
,因此开 dg[20] - 正对角线为红色,截距为
x + y - 反对角线为绿色,截距为
x - y,将它们集体下移就不会出现负数了
这里可以考虑
按行遍历的核心代码:
cpp
// ...
for (int i = 0; i < n; i ++) {
if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
g[u][i] = 'Q'; // u row i col
col[i] = true;
dg[u + i] = true;
udg[n - u + i] = true;
dfs(u + 1);
g[u][i] = '.';
col[i] = false;
dg[u + i] = false;
udg[n - u + i] = false;
}
}- 最优性剪枝(当前一定不如最优解)
- 可行性剪枝(当前一定不可行)
另一种写法,每一格每一格搜索:
首先,按照坐标枚举的时候,防止坐标越界:
cpp
// ...
if (y == n) {
y = 0;
x ++;
}然后在内部有放或者不放皇后两种做法:
- 不放皇后,
y坐标自然增长,待放置皇后个数不变 - 放皇后,
y坐标自然增长,待放置皇后个数少一个
cpp
// ...
dfs(x, y + 1, s); // not put queen
if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {
g[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
dfs(x, y + 1, s + 1); // put queen
g[x][y] = '.';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
}