第五章 学习理论

回顾一下机器学习的基本框架：

• 任务是求出未知的目标函数：$f:\mathcal{X}\to \mathcal{Y}$
• 给出一组训练数据 ${\mathcal{D}}_n=\{({\mathit{x}}_1,y_1),...,({\mathit{x}}_n,y_n)\}$
• 选定一个假设空间 $\mathcal{H}$：一般由先验知识给出
• 通过某个学习算法 $\mathcal{A}$：一般是经验风险最小化 Empirical Risk Minimization，ERM 方法
• 最后找到关于该组训练数据的假设函数 $h_{{\mathcal{D}}_n}\approx f$

这其中有几个理论上的问题：

• 学习是否是可行的？什么条件下是可学习的？
• 是否可以高效地进行学习？如何对学习算法进行理论分析？

统计学习

我们这一代机器学习也被称为统计学习，从统计的视角来看，我们一般会有一些基本假设：

• 数据都是由一个潜在分布 ${\mathcal{D}}_{\mathcal{X}\times \mathcal{Y}}$ 采样得到的
• 训练、测试样本都是由分布 ${\mathcal{D}}_{\mathcal{X}\times \mathcal{Y}}$ 独立同分布采样生成的

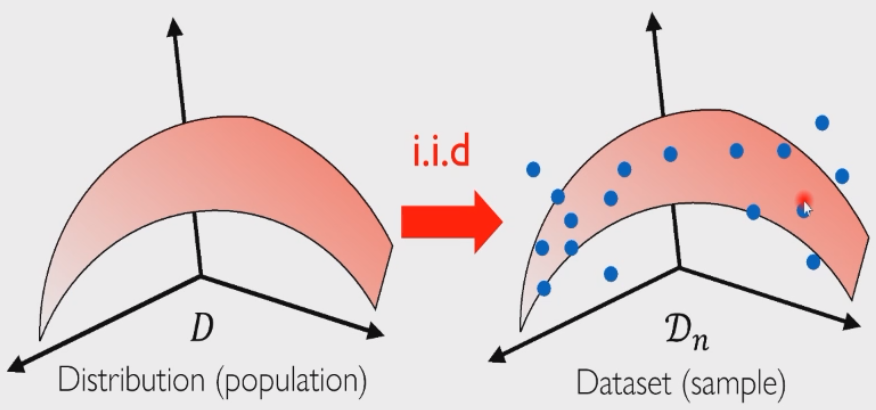
那么这 $n$ 条样本构成的数据集 ${\mathcal{D}}_{\mathcal{n}}$ 能否刻画原数据的潜在分布呢？显然由于采样的随机性，这是不一定的，例如采样数过少就不能表征潜在分布的特点。

独立同分布

首先我们介绍所谓独立同分布 Independent and Identically Distributed，i.i.d 假设：

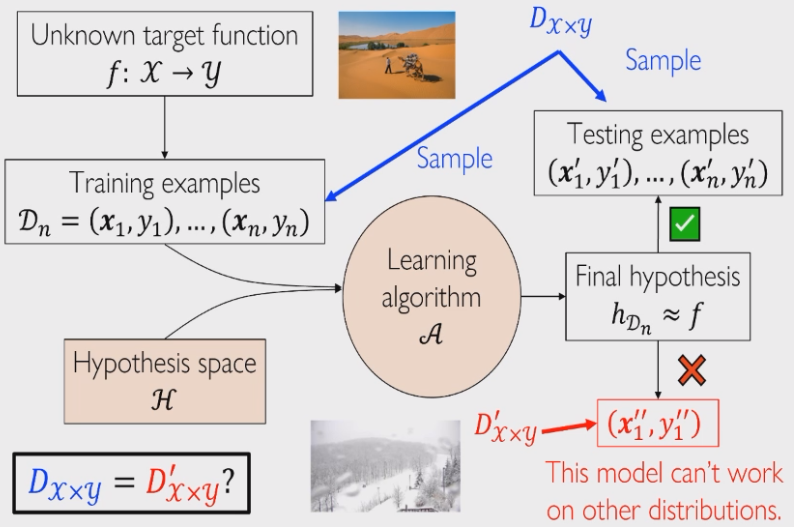
• 首先从潜在分布 ${\mathcal{D}}_{\mathcal{X}\times \mathcal{Y}}$ 中采样得到训练数据 ${\mathcal{D}}_n=\{({\mathit{x}}_1,y_1),...,({\mathit{x}}_n,y_n)\}$
• 然后训练模型，得到我们的假设函数 $h_{{\mathcal{D}}_{\mathcal{n}}}\approx f$
• 之后再从潜在分布 ${\mathcal{D}}_{\mathcal{X}\times \mathcal{Y}}$ 中采样另外一组测试数据 ${\mathcal{D}}_m^{\prime }=\{({\mathit{x}}_1^{\prime },y_1),...,({\mathit{x}}_m^{\prime },y_m)\}$
• 将模型作用到测试数据上，研究模型的预测值和真实值之间的差距

这里面有一个隐藏的假设就是：测试样本和训练样本都是从潜在分布 ${\mathcal{D}}_{\mathcal{X}\times \mathcal{Y}}$ 中独立同分布采样得到的。这是一个严苛的假设，现实世界中的测试样本可能会从另一个潜在分布 ${\mathcal{D}}_{\mathcal{X}\times \mathcal{Y}}^{\prime }$ 中采样得到，如果我们将刚才的模型直接作用过来，一般来说是不能保证得到有效的预测值。因此，测试和训练要从同一分布采样是机器学习/深度学习的一个基本假设，当然有前沿方向研究：迁移学习 Transform Learning，本门课不讲。

泛化

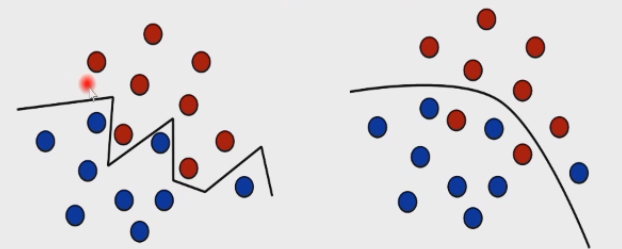
我们知道，学习 learning 和拟合 fitting 不同，例如左图就是一个很好的拟合，但是它不是一个好的学习；右图就是一个很好的学习，但有些点没有完全拟合。二者的区别就在于泛化 generalization 能力。如果一个学习模型在由分布 ${\mathcal{D}}_{\mathcal{X}\times \mathcal{Y}}$ 生成的所有样本中都表现得好 best overall，那么这种模型我们就称之为可泛化的。但是现实中的训练样本总是全体中的一部分，而且还不一定有代表性，因此刻意去拟合一些离群点是不合适的。

这代表了我们的一个偏好：正确的决策面往往不会过于复杂。就好比麦克斯韦方程组，真理往往都是简单的。同样，过于复杂的模型往往会被噪声所干扰，同时也不好解释。

泛化不是记忆，人类学习知识的过程也是泛化的过程，“举一反三”和“触类旁通”就是泛化。机器学习的终极目标就是追求更好的泛化性。现实世界往往需要做一些权衡 trade-off，例如样本大小和模型复杂性之间，以尽量获得好的效果。

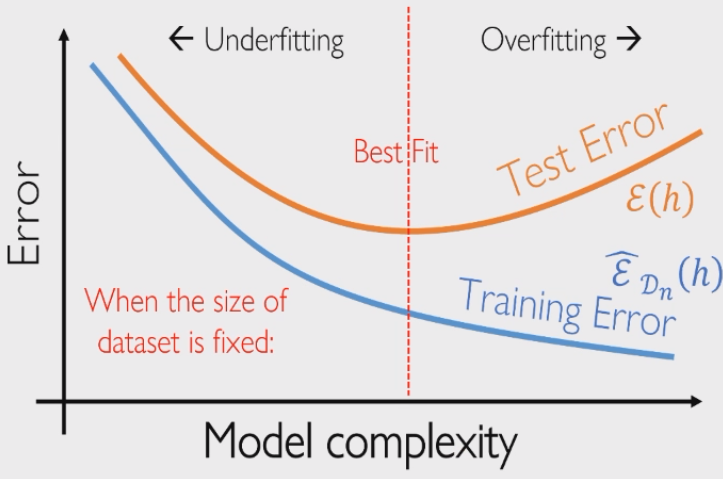
期望误差和经验误差

期望误差 expected error 描述的是：某个假设模型 $h:\mathcal{X}\to \mathcal{Y}$ 在某个分布 $\mathcal{D}$ 上随机采样得到的误差的期望：

$$\mathcal{E}(h)={\mathbb{E}}_{(\mathit{x},y)\sim \mathcal{D}(\mathit{x},y)}\ell (h(\mathit{x}),y)$$

表面上是随机采样了一条样本 $(\mathit{x},y)$，实际上是对分布中所有/无穷条样本求损失函数的平均值。因此期望误差表征了模型在分布全体 population 上的性能。因此机器学习/深度学习/强化学习的终极目标就是降低期望误差。但我们不知道潜在分布 ${\mathcal{D}}_{\mathcal{X}\times \mathcal{Y}}$（概率就是已知分布，统计就是不知道分布，从数据猜测分布，因此机器学习也叫统计机器学习，而不叫概率机器学习）期望误差是放之四海皆准但是却无法计算的准则。

经验误差/训练误差 empirical/training error 描述的是：某个假设模型 $h:\mathcal{X}\to \mathcal{Y}$ 在由分布 $\mathcal{D}$ 上随机采样得到的训练数据集 ${\mathcal{D}}_{\mathcal{n}}$ 中损失函数的平均值：

$${\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)={\displaystyle \frac{1}{n}}\sum _{i=1}^n\ell (h({\mathit{x}}_i),y_i)$$

期望误差和测试误差 test error 之间是否一样？期望误差是在分布 $\mathcal{D}$ 上全体计算得到的，而测试误差仍然只是在分布 $\mathcal{D}$ 上某个样本集计算得到的，只是这个样本集合在训练时是不知道的罢了，因而测试误差只是期望误差的一个近似/代理 proxy。

我们要在测试集上计算模型的测试误差，而如果测试集是一个足够大的随机分布的集合，那么测试误差可以很好地反映期望误差——大数定律。这就引出一个问题：测试集和训练集都要足够大，因此这里也需要做权衡。

经验误差是期望误差的无偏估计，需要对 ${\mathcal{D}}_{\mathcal{n}}$ 求期望，而由于每个样本点都由分布 $\mathcal{D}$ 独立同分布随机采样得到，因此 $n$ 个样本 ${\mathcal{D}}_{\mathcal{n}}\sim {\mathcal{D}}^{\mathcal{n}}$：

$$\mathcal{E}(h)={\mathbb{E}}_{{\mathcal{D}}_{\mathcal{n}}\sim {\mathcal{D}}^{\mathcal{n}}}{\hat{\mathcal{E}}}_{{\mathcal{D}}_{\mathcal{n}}}(h)$$

如果我们知道这个数据集是由 $\mathbb{P}[y|\mathit{x}]$ 生成的，那么我们可以取假设模型为：

$$h_{\text{Bayes}}(\mathit{x})={\text{argmax}}_{y\in \{0,1\}}\mathbb{P}[y|\mathit{x}]$$

即取概率更大的标签作为输出值，这也叫贝叶斯决策准则，此时犯的错误就是最小的。如果这个时候还是犯错了，那么就把这种不可约减的错误率称为贝叶斯错误率：

$${\mathcal{E}}^{\mathcal{\ast }}\triangleq \underset{\mathcal{h}}{min}\mathcal{E}\mathcal{(}\mathcal{h}\mathcal{)}$$

偏差方差分解

定理：对于任何一个样本 $\mathit{x}$，采用模型对其做预测，错误率满足：

$${\mathcal{E}}_{\mathrm{L}2}(\mathit{x})=\mathrm{Var}(y|\mathit{x})+\mathrm{Bias}[h_D(\mathit{x})|\mathit{x}{]}^2+{\mathrm{Var}}_D[h_D(\mathit{x})|\mathit{x}]$$

• $\mathrm{Var}(y|\mathit{x})$：条件方差：随机变量 $y$ 在 $p(y|\mathit{x})$ 下的方差
• ${\mathrm{Var}}_D[h_D(\mathit{x})|\mathit{x}]$：在数据集 $\mathcal{D}$ 上学到一个模型

首先这个定理是在回归问题上推导的，因此损失函数采用 L2 loss，它的微积分性质是最好的。我们记从样本集 ${\mathcal{D}}_{\mathcal{n}}$ 上学习得到的模型为 $h_{{\mathcal{D}}_{\mathcal{n}}}$，那么对于给定的样本数据 $\mathit{x}$，它的预测值为 $h_{{\mathcal{D}}_{\mathcal{n}}}(\mathit{x})$。假定存在一个回归方程为 ${\mathbb{E}}_y[y|\mathit{x}]$，它也是一个条件期望，表示在潜在分布 $\mathcal{D}$ 的意义下，给定样本数据得到的输出值的期望，显然它就是我们所有回归模型想要逼近的目标函数，因此记为：

$${\mathbb{E}}_y[y|\mathit{x}]=f^{\ast }(\mathit{x})$$

由于模型 $h_{{\mathcal{D}}_{\mathcal{n}}}$ 是建立在样本集 ${\mathcal{D}}_{\mathcal{n}}$ 上的，而样本集 ${\mathcal{D}}_{\mathcal{n}}$ 又是随机采样得到的，因此 $h_{{\mathcal{D}}_{\mathcal{n}}}(\mathit{x})$ 也是一个随机变量，它的随机性来自于样本集 ${\mathcal{D}}_{\mathcal{n}}$ 在 $\mathcal{D}$ 上的随机采样。

接下来，我们求这样一个条件期望：${\mathbb{E}}_{{\mathcal{D}}_n,y}[{(h_{{\mathcal{D}}_n}(\mathit{x})-y)}^2|\mathit{x}]$，它指的是模型预测值 $h_{{\mathcal{D}}_{\mathcal{n}}}(\mathit{x})$ 与标签真实值 $y$ 在给定数据点下的二范数误差的期望，也就是回归模型的期望误差（不同训练样本集训练得到的回归模型参数不同）这是对 ${\mathcal{D}}_{\mathcal{n}}$ 和 $y$ 同时求期望：

$$\begin{array}{rl}& {\mathbb{E}}_{{\mathcal{D}}_n,y}[{(h_{{\mathcal{D}}_n}(\mathit{x})-y)}^2|\mathit{x}]\\ =& \mathbb{E}[{(h_{{\mathcal{D}}_n}(\mathit{x})-f^{\ast }(\mathit{x})+f^{\ast }(\mathit{x})-y)}^2|\mathit{x}]\\ =& \mathbb{E}[{(h_{{\mathcal{D}}_n}(\mathit{x})-f^{\ast }(\mathit{x}))}^2+{(f^{\ast }(\mathit{x})-y)}^2+2(h_{{\mathcal{D}}_n}(\mathit{x})-f^{\ast }(\mathit{x}))(f^{\ast }(\mathit{x})-y)|\mathit{x}]\end{array}$$

上式最后一项利用期望的独立性可以写成：

$$2{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})-f^{\ast }(\mathit{x})|\mathit{x}]\cdot {\mathbb{E}}_y[f^{\ast }(\mathit{x})-y|\mathit{x}]=0\Leftarrow {\mathbb{E}}_y[y|\mathit{x}]=f^{\ast }(\mathit{x})$$

因此可以写为：

$${\mathbb{E}}_{{\mathcal{D}}_n,y}[{(h_{{\mathcal{D}}_n}(\mathit{x})-y)}^2|\mathit{x}]={\mathbb{E}}_{{\mathcal{D}}_n}[{(h_{{\mathcal{D}}_n}(\mathit{x})-f^{\ast }(\mathit{x}))}^2\mid \mathit{x}]+{\mathbb{E}}_y[{(f^{\ast }(\mathit{x})-y)}^2\mid \mathit{x}]$$

红色项就是标签噪音，也就是贝叶斯错误率 $\mathrm{Var}(y|\mathit{x})$，不可约减

蓝色项可以写为，加减了 ${\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]=\mathcal{E}\mathcal{(}\mathcal{h}\mathcal{)}$，也就是期望误差：

$$\begin{array}{rl}& {\mathbb{E}}_{D_n}[{(h_{D_n}(\mathit{x})-f^{\ast }(\mathit{x}))}^2\mid \mathit{x}]\\ =& {\mathbb{E}}_{{\mathcal{D}}_n}[{(h_{{\mathcal{D}}_n}(\mathit{x})-{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]+{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]-f^{\ast }(\mathit{x}))}^2\mid \mathit{x}]\\ =& {\mathbb{E}}_{{\mathcal{D}}_n}[{\left(h_{{\mathcal{D}}_n}(\mathit{x})-{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]\right)}^2\mid \mathit{x}]+{\mathbb{E}}_{{\mathcal{D}}_n}[{\left({\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]-f^{\ast }(\mathit{x})\right)}^2\mid \mathit{x}]\\ +& 2{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})-{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]\mid \mathit{x}]\cdot {\mathbb{E}}_{{\mathcal{D}}_n}[{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]-f^{\ast }(\mathit{x})\mid \mathit{x}]\end{array}$$

由于：

$${\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})-{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]\mid \mathit{x}]={\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]-{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]=0$$

因此原式最后只剩前面两项：

$$\begin{array}{rl}& {\mathbb{E}}_{{\mathcal{D}}_n}[{(h_{{\mathcal{D}}_n}(\mathit{x})-{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})])}^2\mid \mathit{x}]+{\mathbb{E}}_{{\mathcal{D}}_n}[{({\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]-f^{\ast }(\mathit{x}))}^2\mid \mathit{x}]\\ =& {\mathbb{E}}_{{\mathcal{D}}_n}[{(h_{{\mathcal{D}}_n}(\mathit{x})-{\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})])}^2\mid \mathit{x}]+{({\mathbb{E}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})]-f^{\ast }(\mathit{x}))}^2\\ =& {\mathrm{Var}}_{{\mathcal{D}}_n}[h_{{\mathcal{D}}_n}(\mathit{x})|\mathit{x}]+\mathrm{Bias}{[h_{{\mathcal{D}}_n}(\mathit{x})|\mathit{x}]}^2\end{array}$$

• 偏差：估计值 $h_{{\mathcal{D}}_n}(\mathit{x})$ 的期望与真实值 $f^{\ast }(\mathit{x})$ 的差距
• 方差：将 $h_{{\mathcal{D}}_n}(\mathit{x})$ 看作随机变量，因此这就是 $h_{{\mathcal{D}}_n}(\mathit{x})$ 的方差/离散度

如果对于不同的训练集，$h_{{\mathcal{D}}_n}(\mathit{x})$ 给出的预测值偏差很大，说明这个模型是不稳定的，因此它代表了模型对不同采样的鲁棒性。综上所述，期望误差的来源有：贝叶斯错误率、偏差的平方以及在不同的训练集上的估计值的方差。

$${\mathcal{E}}_{\mathrm{L}2}(\mathit{x})=\mathrm{Var}(y|\mathit{x})+\mathrm{Bias}[h_{\mathcal{D}}(\mathit{x})|\mathit{x}{]}^2+{\mathrm{Var}}_{\mathcal{D}}[h_{\mathcal{D}}(\mathit{x})|\mathit{x}]$$

因此我们能否找到一个模型，使得上述三项都很小，这样模型的期望误差就很小。遗憾的是，这是不能成立的：

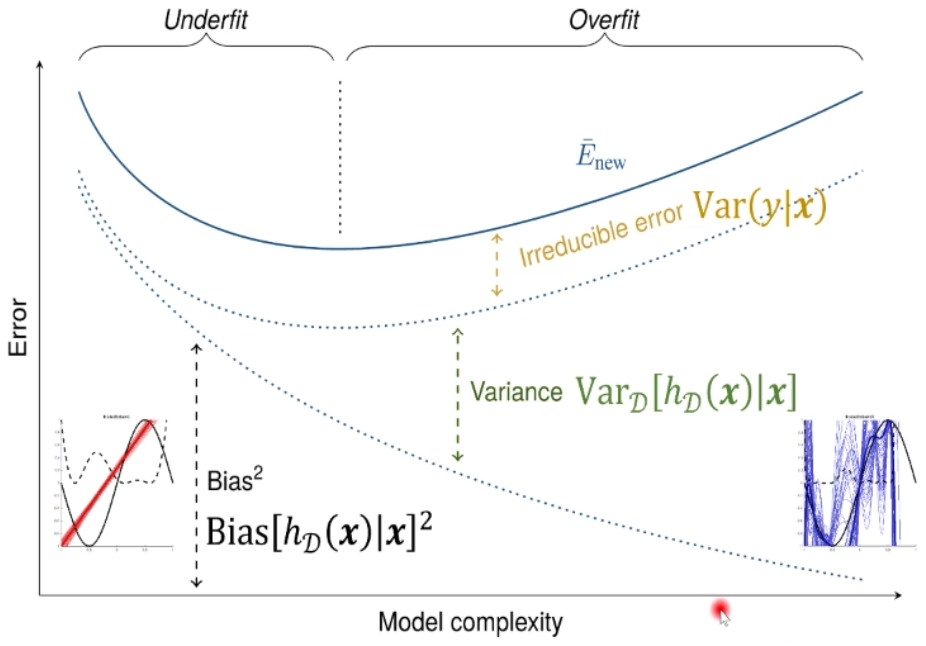
• 贝叶斯错误率是不可约减的 irreducible
• 模型简单时：参数不容易变化，方差小；容易欠拟合，偏差大
• 模型复杂时：参数易发生变化，方差大；拟合较准确，偏差小

偏差方差权衡定理告诉我们：方差和偏差不能同时减小。例如深度学习模型就是用一个非常复杂的模型使得偏差非常小，同时为了避免方差过大，它需要大量的数据用于训练。或者可以使用多个模型做投票/结果求平均值，取均值也会降低方差。

概率近似正确

近似误差与估计误差

偏差方差是在回归问题中推导出来的，而近似误差和估计误差适用于所有机器学习问题：

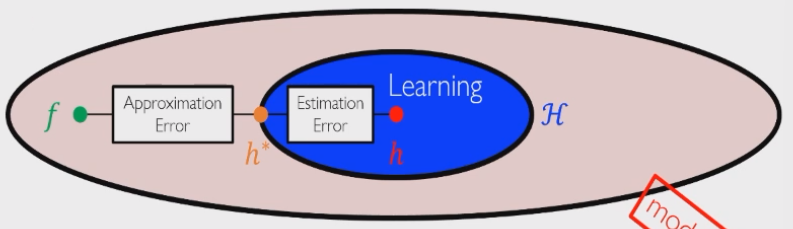
现实中我们只会取到蓝色区域作为假设空间，假设空间中自然存在一个最优的函数 $h^{\ast }$，它与真实函数 $f$ 之间的差距是近似误差 approximation error，近似与随机过程/采样过程无关，是假设空间选定后就确定的量。但我们一般在假设空间中也是找不到这个最优函数 $h^{\ast }$ 的，例如样本数太少，因此最后学习得到的模型 $h$ 和最优模型 $h^{\ast }$ 之间的差距是估计误差 estimation error，表示通过数据进行参数估计产生的误差。

$$\mathcal{E}(h)-{\mathcal{E}}^{\ast }(f)=\underset{\text{estimation}}{\underbrace{[\mathcal{E}(h)-\mathcal{E}(h^{\ast })]}}+\underset{\text{approximation}}{\underbrace{[\mathcal{E}(h^{\ast })-{\mathcal{E}}^{\ast }(f)]}}$$

• 近似误差：表示假设空间的选取优劣程度，是一个确定量
• 估计误差：表示假设函数的选取优劣程度，我们可以给出估计误差的上界

泛化界

估计误差也就是期望误差 $\mathcal{E}\mathcal{(}\mathcal{h}\mathcal{)}$ 与经验误差 ${\mathcal{E}}_{{\mathcal{D}}_{\mathcal{n}}}\mathcal{(}\mathcal{h}\mathcal{)}$ 之差（上面的式子的符号不够严谨）同时我们知道经验误差是期望误差的无偏估计，因此对经验误差求期望就是期望误差。这表示经验误差相对于期望误差的均值为 0，因此我们刻画的是经验误差相对于期望误差的方差，并且我们希望这个随机变量不要太大，也就表示方差不会太大：

$$|{\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)-\mathcal{E}(h)|(\le \epsilon ?)$$

如果这个式子尽量小，说明随着随机变量 ${\mathcal{D}}_{\mathcal{n}}\sim {\mathcal{D}}^{\mathcal{n}}$ 取不同的随机采样点，得到的经验误差不会偏离期望误差太远，也就是泛化能力强。

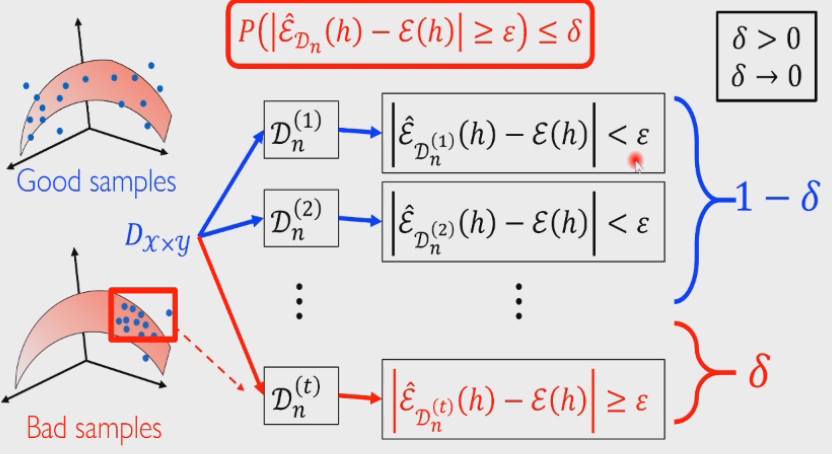
但显然，由于采样具有随机性，我们也许会采样到有偏的一个样本，而且在机器学习中收集数据是很容易发生这种情况的，由此衍生出数据科学 data science 这一门学科。因此我们只能做妥协：希望这个随机变量尽可能满足比较小的性质，也就是随机变量比较大是一个小概率事件：

$$P(|{\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)-\mathcal{E}(h)|\ge \epsilon )\le \delta$$

如果某个学习模型满足：经验误差和期望误差之差大于某个给定常数 $\epsilon$ 是一个小概率事件，那么就可以认为这个学习是以很大的概率成功，也就是可学习的。

PAC 可学习性理论

PAC 学习：概率近似正确学习 Probably Approximately Correct Learning，它是整个机器学习得以实现的基础工作。

一个假设空间 $\mathcal{H}$ 是 PAC 可学习的，如果存在一个算法 $\mathcal{A}$ 和一个多项式函数 $\text{poly()}$，使得存在两个正数 $\epsilon >0,\delta >0$，对于 $\mathcal{X}$ 上的所有分布 $\mathcal{D}$，以及任意一个目标假设 $h\in \mathcal{H}$，在样本复杂度/最少样本数满足 $n\ge \text{poly}(\frac{1}{\epsilon },\frac{1}{\delta },|\mathcal{H}|)$ 时，有下面的不等式成立：

$$P_{{\mathcal{D}}_n\sim {\mathcal{D}}^n}\left[\mathcal{E}(h_{{\mathcal{D}}_n})-\underset{h\in \mathcal{H}}{\min }\mathcal{E}(h)\ge \epsilon \right]\le \delta$$

$\mathcal{E}(h_{{\mathcal{D}}_n})$ 表示在 ${\mathcal{D}}_{\mathcal{n}}$ 上学到的模型在全体分布 $\mathcal{D}$ 上的期望误差。$min\mathcal{E}\mathcal{(}\mathcal{h}\mathcal{)}$ 表示所有模型对应的期望误差中最小的那个。这个概率不等式表示两个期望误差之间（采样得到模型的期望误差与最优模型的期望误差）的差值不会太大，也就是学到的模型足够准确。注意，这些期望误差都是在已知分布 $\mathcal{D}$ 才能算出来的。这其中，红色项被称作近似正确 approximately correct，蓝色项被称作概率正确 probably correct。

到此为止才会发现，概率近似正确是统计学习的上界了。PAC 可学习性理论由图灵奖获得者 Leslie Variant 由 1984 年在《A Theory of the Learnable》中提出。

一般来说，样本条数 $n$ 越大，计算复杂度越高，统计推断复杂度越低。

概率工具

基本性质

并集的上界 Union bound：

$$P(A\cup B)\le P(A)+P(B)$$

概率的反函数：如果有 $P(X\ge \epsilon )\le f(\epsilon )$，那么对于任意 $\delta >0$，有至少 $1-\delta$ 的概率满足：

$$X\le f^{-1}(\delta )$$

证明：记 $\delta =P(X\ge \epsilon )$，那么 $1-\delta =P(X\le \epsilon )$，由于 $f$ 是一个单调递减函数，也就是说：$X\ge \epsilon$ 是一个小概率事件，$\epsilon$ 越大这件事越不容易发生，即 $f(\epsilon )$ 越小，故：

$$X\le \epsilon \le f^{-1}(\delta )$$

既然 $X\le \epsilon$ 发生的概率为 $1-\delta$，那么 $X\le f^{-1}(\delta )$ 发生的概率就有至少 $1-\delta$，证毕。

琴生不等式 Jensen's inequality：如果 $f$ 是一个凸函数，那么有：

$$f(\mathbb{E}[X])\le \mathbb{E}[f(X)]$$

这就是凸函数的定义。

集中不等式

回顾我们在 PAC 学习中的目标（这个似乎和 Variant 的理论不一样？那个是两个期望误差之差，这个是经验误差和期望误差之差，不急，先卖个关子）：

$$P(|{\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)-\mathcal{E}(h)|\ge \epsilon )\le \delta$$

改写上述不等式：即有至少 $1-\delta$ 的概率使得：

$$|{\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)-\mathcal{E}(h)|\le \epsilon \Rightarrow \mathcal{E}(h)\le {\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)+\epsilon$$

这个就是求出了期望误差的上界。注意到期望误差是经验误差的期望，即：$\mathcal{E}(h)={\mathbb{E}}_{D_n}{\hat{\mathcal{E}}}_{D_n}(h)$，我们令 $Z={\mathcal{E}}_{{\mathcal{D}}_n}(h)$，那么不等式转化为如下的集中不等式 concentration inequality 型：

$$P(|Z-\mathbb{E}Z|\ge \epsilon )\le \delta$$

概率中几乎所有的不等式都是集中不等式：大数定律、中心极限定理等等，集中不等式能够控制住随机变量的范围，注意到我们没有对随机变量 $Z$ 做任何假设。

马尔可夫不等式

Markov's Inequality：对于任意一个非负随机变量 $Z$，对任意 $\epsilon >0$，我们有：

$$P(Z\ge \epsilon )\le \frac{\mathbb{E}[Z]}{\epsilon }$$

证明：利用期望的定义，$P_Z(z)$ 是分布函数：

$$\begin{array}{rl}\mathbb{E}[Z]& ={\int }_0^{+\mathrm{\infty }}z\text{ d}{P}_Z(z)\\ & ={\int }_0^{\epsilon }z\text{ d}{P}_Z(z)+{\int }_{\epsilon }^{+\mathrm{\infty }}z\text{ d}{P}_Z(z)\\ & \ge {\int }_0^{\epsilon }0\text{ d}{P}_Z(z)+{\int }_{\epsilon }^{+\mathrm{\infty }}\epsilon \text{ d}{P}_Z(z)\\ & =\epsilon P(Z\ge \epsilon )\end{array}$$

这里要求 $\mathbb{E}[Z]\le +\mathrm{\infty }$，马尔可夫不等式往往用于推导其他的高级不等式。

切比雪夫不等式

Chebyshev's Inequality：如果 $\varphi$ 表示一个非递减的非负函数，$V$ 是一个非负随机变量且有 $\mathbb{E}[V]\le +\mathrm{\infty }$，那么就有：

$$P(V\ge \epsilon )\le P(\varphi (V)\ge \varphi (\epsilon ))\le \frac{\mathbb{E}[\varphi (V)]}{\varphi (\epsilon )}$$

第一个不等式是利用了事件的包含关系，由于 $\varphi$ 表示一个非递减函数，那么就能从 $V\ge \epsilon$ 推导出 $\varphi (V)\ge \varphi (\epsilon )$，因此后面事件发生的概率更大。第二个不等式利用了马尔可夫不等式。实际中取 $\varphi (t)=t^2,V=|Z-\mathbb{E}[Z]|$，就得到了一般意义下的切比雪夫不等式：

$$\begin{array}{rl}P(|Z-\mathbb{E}[Z]|\ge \epsilon )& \le P(|Z-\mathbb{E}[Z]{|}^2\ge {\epsilon }^2)\\ & \le \frac{\mathbb{E}[|Z-\mathbb{E}[Z]{|}^2]}{{\epsilon }^2}\\ & =\frac{\mathrm{Var}(Z)}{{\epsilon }^2}\end{array}$$

切比雪夫不等式就是一个集中不等式：某个随机变量以它均值为核心的事件是一个大概率事件，偏离核心的是一个小概率事件。

弱大数定律

Weak Law of Large Numbers：设 $Z_1,\cdots ,Z_n$ 是独立随机变量序列，它们有着相同的均值 $\mu$ 以及方差 ${\sigma }^2<+\mathrm{\infty }$，记统计量：

$${\overline{Z}}_n=\frac{1}{n}\sum _{i=1}^n{Z}_i$$

因此对于任意的 $\epsilon >0$，有：

$$\underset{n\to \mathrm{\infty }}{lim}P[|{\overline{Z}}_n-\mu |\ge \epsilon ]=0$$

证明：由于 $Z_i$ 独立同分布，利用独立变量的方差和公式：

$$\mathrm{Var}\left[{\overline{Z}}_n\right]=\sum _{i=1}^n\mathrm{Var}\left[\frac{Z_i}{n}\right]=\frac{n{\sigma }^2}{n^2}=\frac{{\sigma }^2}{n}$$

利用切比雪夫不等式，有：

$$P[|{\overline{Z}}_n-\mu |\ge \epsilon ]\le \frac{{\sigma }^2}{n{\epsilon }^2}\to 0(n\to \mathrm{\infty })$$

大数定律在机器学习中基本没有作用，因为 $n\to \mathrm{\infty }$ 是一个不可能的条件。我们需要有限样本 finite-sample 下的结果，但是利用切比雪夫不等式可以得到一个与样本数据 $n$ 有关的上界。

有限样本界

切尔诺夫限

Chernoff Bound：在马尔可夫不等式中，令函数不是二次函数，而是指数函数 $\varphi (t)=e^{\lambda t},\lambda >0$：

$$P(V\ge \epsilon )\le \frac{\mathbb{E}\left[e^{\lambda V}\right]}{e^{\lambda \epsilon }}$$

指数函数的好处就是乘法可以转化为指数相加，适合做极大似然估计。同时我们令 $V=|Z-\mathbb{E}[Z]|$，获得集中不等式：

$$P(Z-\mathbb{E}[Z]\ge \epsilon )\le \frac{\mathbb{E}\left[e^{\lambda (Z-\mathbb{E}[Z])}\right]}{e^{\lambda \epsilon }}$$

如果 $Z$ 是 $n$ 个独立同分布随机变量 $X_i$ 之和，那么有：

$$P(\sum _{i=1}^n(X_i-\mathbb{E}{X}_i)\ge \epsilon )\le \frac{\mathbb{E}\left[e^{\lambda \sum _{i=1}^n(X_i-\mathbb{E}{X}_i)}\right]}{e^{\lambda \epsilon }}=\frac{\prod _{i=1}^n\mathbb{E}\left[e^{\lambda (X_i-\mathbb{E}{X}_i)}\right]}{e^{\lambda \epsilon }}$$

这里运用了独立事件期望的独立性，即 $\mathbb{E}[XY]=\mathbb{E}[X]\mathbb{E}[Y]$，如果事件 $X$ 和 $Y$ 相互独立。

霍夫丁引理

Hoeffding's Lemma：如果 $V$ 是一个有界随机变量且 $\mathbb{E}[V]=0$，并且 $a\le V\le b,b>a$，因此对于任意的 $\lambda >0$：

$$\mathbb{E}\left[e^{\lambda V}\right]\le e^{\frac{{\lambda }^2(b-a{)}^2}{8}}$$

证明：利用指数函数是凸函数的性质，由琴生不等式，函数值小于端点弦上一点：

$$\begin{array}{rl}{e}^{\lambda v}& \le \frac{b-v}{b-a}{e}^{\lambda a}+\frac{v-a}{b-a}{e}^{\lambda b}\end{array}$$

两边对于随机变量 $v$ 取期望，同时注意到 $\mathbb{E}[V]=0$：

$$\begin{array}{rl}\mathbb{E}\left[e^{\lambda V}\right]& \le \mathbb{E}[\frac{b-V}{b-a}{e}^{\lambda a}+\frac{V-a}{b-a}{e}^{\lambda b}]\\ & =\frac{b}{b-a}{e}^{\lambda a}+\frac{-a}{b-a}{e}^{\lambda b}\triangleq e^{\varphi (\lambda )}\end{array}$$

因此我们只需要证明：

$$\varphi (\lambda )=\log [\frac{b}{b-a}{e}^{\lambda a}+\frac{-a}{b-a}{e}^{\lambda b}]\le \frac{{\lambda }^2(b-a{)}^2}{8}$$

证明：对 $\varphi (\lambda )$ 求导（已验算）：

$${\varphi }^{\prime }(\lambda )=a-\frac{a}{\frac{b}{b-a}{e}^{-\lambda (b-a)}-\frac{a}{b-a}}$$

令：

$$\alpha =-\frac{a}{b-a},u=\frac{\frac{-a}{b-a}}{\frac{b}{b-a}{e}^{-\lambda (b-a)}-\frac{a}{b-a}}=\frac{\alpha }{(1-\alpha )e^{-\lambda (b-a)}+\alpha }\le 1$$

原式改写为：

$${\varphi }^{\prime }(\lambda )=a+(b-a)u,1-u=\frac{(1-\alpha )e^{-\lambda (b-a)}}{(1-\alpha )e^{-\lambda (b-a)}+\alpha }$$

求导（已验算）：

$${\varphi }^{\prime \prime }(\lambda )=u(1-u)(b-a{)}^2\le \frac{(b-a{)}^2}{4}$$

注意到：$\varphi (0)=0,{\varphi }^{\prime }(0)=0$，因此存在 $0\le \theta \le \lambda$ 使得（二阶泰勒展开的带拉格朗日余项的形式）：

$$\varphi (\lambda )=\varphi (0)+\lambda {\varphi }^{\prime }(0)+\frac{{\lambda }^2}{2}{\varphi }^{\prime \prime }(\theta )\le \frac{{\lambda }^2(b-a{)}^2}{8}$$

霍夫丁不等式

Hoeffding's Inequality：对于 $n$ 个随机变量 $a_i\le X_i\le b_i$，记 $V_i=X_i-\mathbb{E}[X_i]$，由于：$\mathbb{E}[V_i]=0$，利用切尔诺夫限与霍夫丁引理有：

$$\frac{\prod _{i=1}^n\mathbb{E}\left[e^{\lambda (X_i-\mathbb{E}{X}_i)}\right]}{e^{\lambda \epsilon }}\le \frac{e^{\sum _{i=1}^n\left[\frac{{\lambda }^2{(b_i-a_i)}^2}{8}\right]}}{e^{\lambda \epsilon }}=e^{[\frac{\sum _{i=1}^n{\lambda }^2{(b_i-a_i)}^2}{8}-\lambda \epsilon ]}$$

可以看到指数项是一个关于 $\lambda$ 的二次函数，我们求其对称轴：

$${\lambda }^{\ast }=\arg \underset{\lambda }{min}\frac{\sum _{i=1}^n{\lambda }^2{(b_i-a_i)}^2}{8}-\lambda \epsilon =\frac{4\epsilon }{\sum _{i=1}^n{(b_i-a_i)}^2}$$

代入上式就求到了最紧的一个限：

$$\begin{array}{rl}P(\sum _{i=1}^n(X_i-\mathbb{E}{X}_i)\ge \epsilon )& \le \frac{\prod _{i=1}^n\mathbb{E}\left[e^{\lambda (X_i-\mathbb{E}{X}_i)}\right]}{e^{\lambda \epsilon }}\\ & \le \exp [\frac{\sum _{i=1}^n{\lambda }^2{(b_i-a_i)}^2}{8}-\lambda \epsilon ]\\ & \stackrel{min}{⟹}\exp [-\frac{2{\epsilon }^2}{\sum _{i=1}^n{(b_i-a_i)}^2}]\end{array}$$

• 第一个不等式：切尔诺夫限
• 第二个不等式：霍夫丁引理
• 第三个不等式：二次函数的最小值

最后，如果我们用 $-X_i\in [-b_i,-a_i]$ 替换掉 $X_i$，同样可以得到一个上界：

$$P(\sum _{i=1}^n(X_i-\mathbb{E}{X}_i)\le -\epsilon )\le \exp [-\frac{2{\epsilon }^2}{\sum _{i=1}^n{(b_i-a_i)}^2}]$$

加起来写成绝对值的形式，就得到了最终的霍夫丁不等式，对于 $n$ 个随机变量 $a_i\le X_i\le b_i$：

$$P(\left|\sum _{i=1}^n(X_i-\mathbb{E}{X}_i)\right|\ge \epsilon )\le 2\exp [-\frac{2{\epsilon }^2}{\sum _{i=1}^n{(b_i-a_i)}^2}]$$

$n$ 个随机变量之和与它们的期望之和的差，如果它 $\ge \epsilon$ 这个事件发生是有概率上界的，而且是一个有限样本的界，哪怕 $n=1$ 都成立。

麦克迪尔米德不等式

McDiarmid's Inequality：（霍夫丁不等式的推广版本）记 $X_1,\cdots ,X_n\in \mathcal{X}$ 是独立同分布的随机变量，存在一个以它们这些随机变量为自变量的函数 $f:{\mathcal{X}}^n\to \mathbb{R}$，同时要求这个函数对自变量变化是稳定的，即：

$$\underset{x_1,x_2,\dots ,x_n,x_i^{\prime }}{sup}|f(x_1,\dots ,x_i,\dots ,x_n)-f(x_1,\dots ,x_i^{\prime },\dots ,x_n)|\le c_i$$

自变量发生了变化，但函数值的变化始终有上界 $c_i$。那么对于任意 $\epsilon >0$，我们就有下面的不等式成立：

$$P(|f(X_1,\dots ,X_n)-\mathbb{E}f(X_1,\dots ,X_n)|\ge \epsilon )\le 2\exp (-\frac{2{\epsilon }^2}{\sum _{i=1}^n{c}_i^2})$$

如果令函数 $f$ 是均值函数，且：

$$f(x_1,\dots ,x_i,\dots ,x_n)=\frac{1}{n}\sum _{i=1}^n{x}_i,c_i=\frac{|b_i-a_i|}{n}$$

此时就可以得到霍夫丁不等式（即 $\epsilon \to n\epsilon$）。

麦克迪尔米德不等式就是有限样本情况下的集中不等式：它表示了任意一个随机变量 $f$ 与它的期望之间的差/偏离程度超过 $\epsilon$ 是一个小概率事件。同时可以发现：它的准确的上界是一个关于 $\epsilon$ 的减函数，如果 $\epsilon$ 越大，上界就越小，即偏离程度过大是一个小概率事件。又注意到，这个上界与 $c_i$ 的关系是一个增函数，即 $c_i$ 越大，也即 $f$ 越不稳定，也就越容易导致函数值和均值之间的偏离程度超过 $\epsilon$，上界就越大。同时也是关于 $n$ 的增函数？卖个关子。

因此只有当 $\epsilon$ 比较大，同时 $c_i$ 比较小的时候，这个上界才会趋近于 0，也就是说：稳定函数且距离均值中心较远这一事件所发生的概率很低。由此我们看到：麦克迪尔米德不等式就是一个放之四海而皆准的不等式。例如可以套用经验误差和期望误差。

有限假设空间上的泛化界

单假设函数

有限假设空间 Finite Hypothesis Space：$|\mathcal{H}|<\mathrm{\infty }$。回顾霍夫丁不等式：

$$P(\left|\sum _{i=1}^n(X_i-\mathbb{E}{X}_i)\right|\ge \epsilon )\le 2\exp [-\frac{2{\epsilon }^2}{\sum _{i=1}^n{(b_i-a_i)}^2}]$$

如果令随机变量 $X_i=\ell (h\left({\mathit{x}}_i\right),y_i)$ ，即任何一条样本数据在模型 $h$ 上的损失函数值（随机性由样本点给出），那么对于所有训练数据 $(x_i,y_i)\in {\mathcal{D}}_n$ ：

$$\begin{array}{rl}\sum _{i=1}^n(X_i-\mathbb{E}{X}_i)& =n\{\left[\frac{1}{n}\sum _{i=1}^n\ell (h\left({\mathit{x}}_i\right),y_i)\right]-{\mathbb{E}}_{(x,y)\sim \mathcal{D}}\ell (h(\mathit{x}),y)\}\\ & =n({\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)-\mathcal{E}(h))\end{array}$$

$n$ 是一个提到外面的一个系数，这个更直观地反映了期望误差就是经验误差的期望。这里需要引入一个假设：要求损失函数是有界的，因为霍夫丁不等式和麦克迪米尔德不等式都要求损失函数有界，即： $\ell (h(\mathit{x}\ast i),y\ast i)\in [0,1]=[a_i,b_i]$（这里不讨论无界的损失函数，合页损失函数 Hinge Loss 就是无界损失函数，但是我们后面会证明采用无界损失函数学习得到的模型与采用有界损失函数学习得到的模型是一样的 —— 叫做一致性，即换一个损失函数学到的模型与原来的损失函数学到的模型是一样的），代入霍夫丁不等式得到：

$$P(n|{\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)-\mathcal{E}\mathcal{(}\mathcal{h}\mathcal{)}|\ge \epsilon )\le 2e^{-\frac{2{\epsilon }^2}{n}}$$

我们可以控制住经验误差与期望误差的差！再用 $n\epsilon$ 替代 $\epsilon$，这个式子就变成了：

$$P(|{\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)-\mathcal{E}\mathcal{(}\mathcal{h}\mathcal{)}|\ge \epsilon )\le 2e^{-\frac{2n^2{\epsilon }^2}{n}}=2e^{-2n{\epsilon }^2}$$

回顾概率的反函数性质（右边是减函数），我们令：

$$\delta =P(|{\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)-\mathcal{E}(h)|\ge \epsilon )\le 2e^{-2n{\epsilon }^2}\Rightarrow \epsilon \le \sqrt{\frac{\log \frac{2}{\delta }}{2n}}$$

因此反事件就有至少 $1-\delta$ 的概率，对于任意采样 ${\mathcal{D}}_{\mathcal{n}}$，使得 $|{\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)-\mathcal{E}(h)|\le \epsilon$ 发生，或者：

$$\mathcal{E}(h)\le {\hat{\mathcal{E}}}_{{\mathcal{D}}_n}(h)+\sqrt{\frac{\log \frac{2}{\delta }}{2n}}$$

这就是期望误差 $\mathcal{E}(h)$ 的上界，也被称为有限假设空间下的泛化误差界。期望误差的界可以被经验误差界定。

多假设函数

无限假设空间上的泛化界

线性分类器的泛化界

采样的随机性导致的模型的随机性，因此模型的经验误差需要和期望误差之间不能差的太远。