第四章 支持向量机

支持向量机

支持向量机 Support Vector Machine。

首先，我们再重新思考一下如何二分类？对于高维空间中的样本点，要将它们分开来，一个几何视角就是：找到一个超平面，将它们分开。注意，超平面自然是一个线性模型，但是我们之前研究线性模型更多的是从统计观点来看的，现在我们就从几何视角入手。

我们不在用 $\{0,1\}$ 表示类别，改用 $\{-1,+1\}$ 来表示类别。用 $h(\mathit{x})=\mathit{w}\cdot \mathit{x}+b$ 表示预测值。由于超平面对应 $\mathit{w}\cdot \mathit{x}+b=0$，那么点在上半平面就是 $\mathit{w}\cdot \mathit{x}+b>0$，而如果此时真实值 $y$ 也在上半平面，那么 $y=+1$，对应的就是 $y(\mathit{w}\cdot \mathit{x}+b)>0$。因此分类的 01 损失函数为：

• 分对了：$\mathbf{1}[h(\mathit{x})\ne y]=0$，即 $y(\mathit{w}\cdot \mathit{x}+b)>0$
• 分错了：$\mathbf{1}[h(\mathit{x})\ne y]=1$，即 $y(\mathit{w}\cdot \mathit{x}+b)<0$

标签值和样本之于超平面所处的位置是否一致：标签为正表示样本在超平面上半部分：

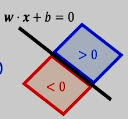
问题：怎样去选择最好的分类器/超平面？之前在统计的意义下已经解决了这个问题。现在我们从几何视角下回顾：

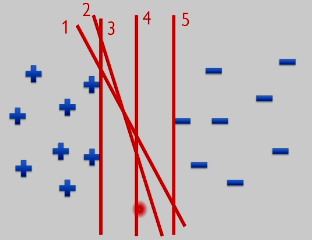
显然 4 号超平面是最好的，因为它离所有样本最远。计算点到超平面的距离！找一个最大间隔 margin 的超平面，它对于噪声数据的鲁棒性最强。那么如何确定带有最大间隔的超平面呢？首先要找到一个正例的上夹板和负例的下夹板，使得上夹板和下夹板之间的间隔达到最大，将其称之为 margin，居中的超平面就是我们要找的超平面。（最小间隔，最大间隔，平均间隔？）

间隔：距离两个类中最近的点之间的距离称为间隔：也被称为 最小间隔。

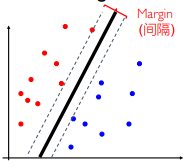
需求：

• 间隔尽量大
• 所有的点都分对

$$\begin{array}{rl}& \underset{\mathit{w},b}{max}\mathrm{margin}(\mathit{w},b)\\ \text{s.t. }& y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\ge 1,1\le i\le n\end{array}$$

这里的 1 是一个 裕度。如果我们说 $y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\ge 0$，那么上下夹板就重合了。其中，裕度也可以看作一种抗噪声能力（统计意义下的置信度就对应几何下的间隔 margin，#TODO 但是我现在觉得裕度没啥用）：

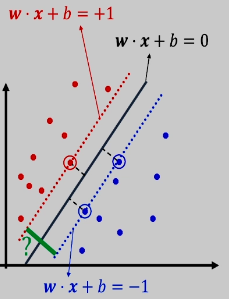
点到平面的距离公式

定理：设平面外的一点 ${\mathit{x}}_0$，求它到以 $\mathit{w}$ 为法向量，以 $b$ 为截距的超平面之间的距离：

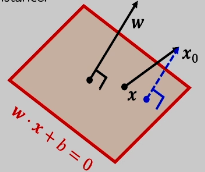
设超平面上有一点 $\mathit{x}$，则它一定满足 $\mathit{w}\cdot \mathit{x}+b=0$，同时它到 ${\mathit{x}}_0$ 的向量为 ${\mathit{x}}_0-\mathit{x}$，那么所求的就是它在法向量 $\mathit{w}$ 上的投影：

$$\begin{array}{rl}\left|{\mathrm{Proj}}_{\mathit{w}}({\mathit{x}}_0-\mathit{x})\right|& =\frac{|\mathit{w}\cdot ({\mathit{x}}_0-\mathit{x})|}{\parallel \mathit{w}\parallel }\\ & =\frac{|\mathit{w}\cdot x_0-\mathit{w}\cdot \mathit{x}|}{\parallel \mathit{w}\parallel }\\ & =\frac{|\mathit{w}\cdot {\mathit{x}}_0+b|}{\parallel w\parallel }\end{array}$$

Project 就是投影。我们再以二维向量来说明这个间隔：

首先，满足 $y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\ge 1$ 一定存在吗？是一定的，因为超平面也就是 $\mathit{w}\cdot {\mathit{x}}_i+b=0$，那么我们在构造的时候不妨这么思考，该超平面一定可以转化为 $w_0^{\prime }+w_1^{\prime }{x}_1+x_2=0$，以 $x_2$ 为纵轴的话，那么截距就是 $-w_0^{\prime }$。而我们知道原超平面是 $w_1{x}_1+w_2{x}_2+b=0$，以正例为例的话，所求的上夹板就是 $w_1{x}_1+w_2{x}_2+b=1$，截距就是 $(1-b)/w_2$，斜率为 $-w_1/w_2$，想要找一个这样的直线自然是轻而易举。因为对于某两个分属于正负例的点而言，它们之间的间隔可以小的近乎为 0（也就是穿过二者的直线，这样上下夹板重合），也可以得到一条这样要求的直线。

但是问题就在于：找到了上夹板，那么下夹板就一定存在吗？不一定，举一个极端的例子来看：假设正例全部分布在 $x_2=2x_1+1$ 上，负例全部分布在 $x_2=2x_1$ 上。那么永远无法找到合适的夹板。

于是我们这里就又有了一个前提：这样的夹板是可以找到的。那么样本点中离分类面最近的点最近的所在只能是在上下夹板上，即 $\mathit{w}\cdot \mathit{x}+b=\pm 1$，也就是说：虽然不能保证上下夹板上一定都有样本点，但是这是可以被允许的最近距离。因此总间隔为：

$$\gamma =\frac{1}{\parallel \mathit{w}{\parallel }_2}+\frac{|-1|}{\parallel \mathit{w}{\parallel }_2}=\frac{2}{\parallel \mathit{w}{\parallel }_2}$$

这里求的间隔不是到点的间隔，或者穿过点的直线的间隔，而就是到裕度为 1 的上下夹板之间的间隔。当然我们最后所求的最大值一定能够满足至少一个夹板上有数据点：

$$\begin{array}{rl}& \underset{\mathit{w},b}{max}\frac{2}{\parallel \mathit{w}{\parallel }_2}\\ \text{s.t. }& y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\ge 1,1\le i\le n\end{array}$$

在我们实现了这个约束条件的时候，就说明我们创造了两个夹板，并不需要夹板上有没有数据点，我们所求的最大值也是夹板间的间隔最大值。例如只有两个点 $(0,2)$ 和 $(2,0)$，对应的“间隔”最大值显然是 $2\sqrt{2}$，超平面显然是 $y=x$ 最佳。

$\mathit{w}\cdot \mathit{x}+b=1$ 和 $\mathit{w}\cdot \mathit{x}+b=-1$ 就是两个夹板。但这并不代表着夹板之间的截距是 2，而是 $2/w_2$，通过调整 $w_2$ 的值可以使得任何这样的夹板都是可以找到的，例如假设正例全部分布在 $x_2=x_1+1$ 上，负例全部分布在 $x_2=x_1$ 上。也可以找到。

任意给两个点都能找到恰好满足 $\mathit{w}\cdot \mathit{x}+b=1$ 和 $\mathit{w}\cdot \mathit{x}+b=-1$ 的上下夹板。数据集中距离最近的那两个点一定会在上下夹板上。因为夹板就是三个未知数两个方程，说明夹板有无穷多组满足的解，在其中找出使得所求间隔最大的解 —— 其实就是穿过这两个点的平行线族。

$$\{\begin{array}{l}{w}_1{x}_1+w_2{x}_2+b=1\\ w_1{x}_1^{\prime }+w_2{x}_2^{\prime }+b=-1\end{array}$$

这也被称为硬间隔支持向量机 High-margin SVM：

$$\begin{array}{rl}& \underset{\mathit{w},b}{min}\frac{1}{2}\parallel \mathit{w}{\parallel }_2^2\\ \text{s.t. }& y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\ge 1,1\le i\le n\end{array}$$

• 1/2 为了方便计算
• $\parallel \mathit{w}{\parallel }_2$ 不是凸函数，但是 $\parallel \mathit{w}{\parallel }_2^2$ 是凸函数

这是一个 线性约束的二次优化问题。前面的都是线性可分的数据 —— 很强的假设。

线性不可分情况下的分类

线性不可分或者过拟合的情况：

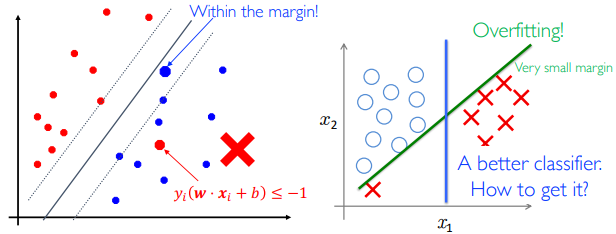
不能过分要求线性可分：允许一部分点在错误的那一边。但是在错误那一边点的数量不能多。因此：

$$\begin{array}{rl}& \underset{\mathit{w},b}{min}\frac{1}{2}\parallel \mathit{w}{\parallel }_2^2\\ \text{s.t. }& y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\ge 1-{\xi }_i,\xi \ge 0,\sum _{i=1}^n\xi \le n^{\prime },1\le i\le n\end{array}$$

我们称 ${\xi }_i$ 为松弛变量 Slack Variables。

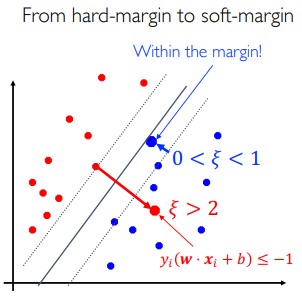
收益就是间隔可以更大了，是一种权衡犯错点数量和间隔大小的方法：将约束的和式放到目标函数上（软间隔支持向量机的目标函数）：

$$\begin{array}{rl}& \underset{\mathit{w},b,\mathit{\xi }}{min}\frac{1}{2}\parallel \mathit{w}{\parallel }_2^2+C\sum _{i=1}^n{\xi }_i\\ \text{s.t. }& y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\ge 1-{\xi }_i,{\xi }_i\ge 0,1\le i\le n\end{array}$$

对任何的 $n^{\prime }$ 都存在对应的 $C$（不等式约束下的拉格朗日乘数法）。${\xi }_i$ 可以理解为错误。对于错误的 L1 正则化。

支持向量机无法做多分类任务：几何直观模型的天然局限，还会存在 Ambiguity 死角。

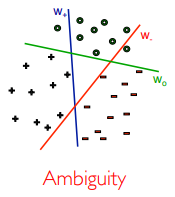
对于 $m$ 个类，我们引入 $m$ 个超平面，One-vs-Rest：对于每个超平面，将一类作为正例，其余都是负例。对于测试用例，我们根据所有的超平面进行投票：但是对于死角的情况（所有的超平面都给出了负例），SVM 是无法解决的。不同的超平面得到的 score 是无法比较的，超参数 $C$ 不同导致分类错误率不同，放在一起比较是没有意义的。trade-off！

支持向量机的重要性：

• 学科发展
• 引入的最大间隔思想
• 引入的核函数方法

默认的软件包将超参数 $C$ 置为 1，人们一般按照 2 的指数进行网格搜索。机器学习中调参一般就是等间隔网格或者指数网格。

联合优化

将 $m$ 个超平面放在一起优化：

$$\begin{array}{rl}& \underset{\left\{{\mathit{w}}_j\right\},\left\{b_j\right\},\mathit{\xi }}{min}\frac{1}{2}\sum _{j=1}^M{\Vert {\mathit{w}}_j\Vert }_2^2+C\sum _{i=1}^n{\xi }_i\\ \text{s.t. }& \mathrm{\forall }j\ne y_i,{\mathit{w}}_{y_i}\cdot {\mathit{x}}_i+b_{y_i}\ge {\mathit{w}}_j\cdot {\mathit{x}}_i+b_j+1-{\xi }_i,{\xi }_i\ge 0,i\in [n]\end{array}$$

超平面下本类的 score：${\mathit{w}}_{y_i}\cdot {\mathit{x}}_i+b_{y_i}$，其他类的 score：${\mathit{w}}_j\cdot {\mathit{x}}_i+b_j$，同时还要大一个软间隔：$1-{\xi }_i$，即便如此，这个模型是无法输出概率，后面还需要一个 Softmax 函数 —— 那为啥不直接用 Softmax Regression？人们平时采用的贝叶斯准则就是基于概率的 —— 这是很朴素的。

约束优化问题

凸优化

Convex Optimization：SVM 是一个线性约束的二次优化问题。高中数学中，一般都是固定一组变量就是求另外一组的最小值。

$$\begin{array}{rl}& \underset{x}{min}f(x)\\ & \text{s.t. }x\in \mathcal{X}\end{array}$$

• $\mathcal{X}$ 是一个凸集，$f(x)$ 是一个凸函数
• 凸集 $S$ 的定义：$x,x^{\prime }\in S\Rightarrow \mathrm{\forall }\lambda \in [0,1],\lambda x+(1-\lambda )x^{\prime }\in S$：两点连线在集合内
• 凸函数 $f(x)$ 的定义：$\mathrm{\forall }\lambda \in [0,1],x,x^{\prime }\in \mathrm{dom}(f):f(\lambda x+(1-\lambda )x^{\prime })\le \lambda f(x)+(1-\lambda )f\left(x^{\prime }\right)$：割线在弧的上方

如果：

• $\mathcal{X}={\mathbb{R}}^d$，那么就是一个不带约束的优化问题，微积分求导即可
• $\mathcal{X}\subset {\mathbb{R}}^d$，且是一个凸集合，那么这就是带约束的优化问题 Constrained Problem

等式约束

可以将约束写为如下形式：

$$\begin{array}{rl}& \underset{\mathit{x}\in {\mathbb{R}}^d}{min}f(\mathit{x})\\ & \text{s.t. }g(\mathit{x})=0\end{array}$$

首先，如果是无约束优化问题，那么最小值对应的就应该是 $\mathrm{\nabla }f(\mathit{x})=0$ 的点。而此时我们要求所有的点都需要满足 $g(\mathit{x})=0$：这个时候假设约束函数 $g(\mathit{x})=0$ 为红色的线，那么我们画出在某一点的切线 ${\mathrm{\nabla }}_{\mathit{x}}g(\mathit{x})$，导数是垂直于切线的（因为导数是因变量关于自变量的变化率，当我们沿着切线走的时候，由于函数值恒等于 0，因此它的变化率也为 0，因此导数就应该和我们走的方向正交，导数就是沿着导数的方向，因变量会随着自变量而变化）

其次，我们考虑最优的点 ${\mathit{x}}^{\ast }$，首先它需要满足 $g({\mathit{x}}^{\ast })=0$，考虑 ${\mathrm{\nabla }}_{\mathit{x}}f({\mathit{x}}^{\ast })$，如果它不是垂直于切线的，那么我们沿着切线的方向走（就相当于在 $g(\mathit{x})=0$ 上走），$f(\mathit{x})$ 的值就会发生变化！因此最优点 ${\mathit{x}}^{\ast }$ 处 $f(\mathit{x})$ 的导数也是垂直于切线的。

上面一个条件是对于所有点成立的，下面一个条件只对于最优点成立。那么既然二者是平行关系，那么存在一个 $\mu$ 使得：

$$\mathrm{\nabla }f+\mu \mathrm{\nabla }g=0,\mu \ne 0$$

其实就是关于 $f+\mu g$ 求导，记拉格朗日函数为：

$$L(\mathit{x},\mu )=f(\mathit{x})+\mu g(\mathit{x})$$

拉格朗日函数有两个变量，分别求导数：

$$\begin{array}{rl}& {\mathrm{\nabla }}_{\mathit{x}}L=0\iff \mathrm{\nabla }f+\mu \mathrm{\nabla }g=0\\ & \frac{\partial }{\partial \mu }L=0\iff g(\mathit{x})=0\end{array}$$

对两个变量的导数都为 0 才是驻点。拉格朗日函数的驻点就是所求的最优点。

不等式约束

Inequality Constraints

$$\begin{array}{rl}& \underset{\mathit{x}\in {\mathbb{R}}^d}{min}f(\mathit{x})\\ & \text{s.t. }g(\mathit{x})\le 0\end{array}$$

如果最优解在区域内部，那么约束失效，求解关于 $f(\mathit{x})$ 的导数即可。它是拉格朗日函数中 $\mu =0$ 的情况。另外一种情况最优解在边界上，这与等式约束相同，但是这里要求 $\mu >0$，要求导函数反向，同时要求 $\mathrm{\nabla }f(\mathit{x})$ 的方向要指向区域内部（导数的方向就是函数值增加最快的方向，因此如果指向了外部，那么内部必然存在一个使得函数值更小的点，这是不合适的，而指向内部的话，说明使得函数值更小的点在区域外部，那么区域上就是可行的最优解）由于 $\mathrm{\nabla }g(\mathit{x})$ 的方向始终指向区域的外部，因此 $\mu >0$。

总结得到 KKT 条件（Karush-Kuhn-Tucker Conditions）：对于拉格朗日函数：$ L(\boldsymbol{x}, \lambda)=f(\boldsymbol{x})+\lambda g(\boldsymbol{x}) $，它需要满足：

• $g(\mathit{x})\le 0$：Primal Feasibility 原问题的可行解区域
• $\lambda \ge 0$：Dual Feasibility 对偶可行解区域（新引入的变量 $\lambda$ 称为对偶变量）
• $\lambda g(\mathit{x})=0$：Complementary Slackness 补充松弛变量（将内部解和边界解写在一起）

一般意义的拉格朗日函数

考虑如下的原问题：

$$\begin{array}{rl}& \underset{\mathit{x}\in {\mathbb{R}}^d}{min}f(\mathit{x})\\ \text{s.t. }& g_j(\mathit{x})\le 0\text{ for }j=1,\cdots ,J\\ \text{s.t. }& h_k(\mathit{x})=0\text{ for }k=1,\cdots ,K\end{array}$$

优化问题的正规性条件：#TODO

$$L(\mathit{x},\mathit{\lambda },\mathit{\mu })=f(\mathit{x})+\sum _{j=1}^J{\lambda }_j{g}_j(x)+\sum _{k=1}^K{\mu }_k{h}_k(\mathit{x})$$

为什么是加起来？因为都要满足导数互相平行的关系！得到推广的 KKT 条件，对于所有的 $1\le j\le J$：

• Primal Feasibility：$ g_{j}(\boldsymbol{x}) \leq 0, h_{k}(\boldsymbol{x})=0 $
• Dual Feasibility：${\lambda }_j\ge 0$
• Complementary Slackness：${\lambda }_j{g}_j(\mathit{x})=0$

求导：

$${\mathrm{\nabla }}_{\mathit{x}}f(\mathit{x})+\sum _{j=1}^J{\lambda }_j{\mathrm{\nabla }}_x{g}_j(\mathit{x})+\sum _{k=1}^K{\mu }_k{\mathrm{\nabla }}_x{h}_k(\mathit{x})=\mathbf{0}$$

如果求到的三个驻点 ${\mathit{x}}^{\ast },{\mathit{\mu }}^{\ast },{\mathit{\lambda }}^{\ast }$ 均满足 KKT 条件，那么 ${\mathit{x}}^{\ast }$ 就是最优解：

$$f\left({\mathit{x}}^{\ast }\right)=L({\mathit{x}}^{\ast },{\mathit{\lambda }}^{\ast },{\mathit{\mu }}^{\ast })$$

原问题和对偶问题

根据拉格朗日函数引出的原问题和对偶问题，首先来看原问题：

$$\begin{array}{rl}& \underset{\mathit{x}\in {\mathbb{R}}^d}{min}f(\mathit{x})\\ \text{s.t. }& g_j(\mathit{x})\le 0\text{ for }j=1,\cdots ,J\\ \text{s.t. }& h_k(\mathit{x})=0\text{ for }k=1,\cdots ,K\end{array}$$

那么它的拉格朗日对偶问题为：

$$\begin{array}{rl}& \underset{\mathit{\lambda }\in {\mathbb{R}}^J,\mathit{\mu }\in {\mathbb{R}}^K}{max}\mathrm{\Gamma }(\mathit{\lambda },\mathit{\mu })\triangleq \underset{\mathit{x}}{inf}L(\mathit{x},\mathit{\lambda },\mathit{\mu })\\ & \text{s.t. }{\lambda }_j\ge 0\text{ for }j=1,\dots ,J\end{array}$$

什么是 $\underset{\mathit{x}}{inf}L(\mathit{x},\mathit{\lambda },\mathit{\mu })$，它表示对 $\mathit{x}$ 求完 最小值 之后的拉格朗日函数（将 $\mathit{\lambda },\mathit{\mu }$ 都看作常数）。

原来的函数的自变量是 $\mathit{x}$，现在的自变量变成拉格朗日乘子了。注意，虽然没写 Complementary Slackness，但是最后还是要考虑。注意拉格朗日对偶函数 $\mathrm{\Gamma }(\mathit{\lambda },\mathit{\mu })$ 永远是一个凹函数，不管原先的函数是不是凸函数 —— 对偶问题的求解比原问题的求解性质更好。并且对偶问题的约束条件也是凸的。

定理：如果对一个仿射函数（线性函数）的点点最小值是一个凹函数。https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf，显然，拉格朗日函数是关于对偶变量的仿射函数。SVM 是一种带约束的优化问题，引入拉格朗日对偶问题的收益有限，因为 SVM 的约束很好。

如果原问题是凸问题，那么对偶问题和原问题的解相同；如果原问题不是凸问题，由于拉格朗日对偶问题是凸问题，那么二者之间的最优解存在一个 gap，称之为 拉格朗日间隔。只有近似解足够好，拉格朗日间隔足够小，我们就认为可以接受。

如何消去 $\mathit{x}$？

$${\mathrm{\nabla }}_{\mathit{x}}L=0\Rightarrow \mathit{x}=\psi (\mathit{\lambda },\mathit{\mu })$$

万一无法求出 $\psi (\mathit{\lambda },\mathit{\mu })$ 怎么办？也就是无法求出 $\mathit{x}$ 的闭式解 —— 线性约束二次优化问题不存在这个困扰。

如果 $\overline{\mathit{x}}$ 是满足约束条件的任意的点，那么有：

$$\underset{\mathit{x}}{inf}L(\mathit{x},\lambda ,\mathit{\mu })\le f(\bar{\mathit{x}})+\sum _{j=1}^J{\lambda }_j{g}_j(\overline{x})+\sum _{k=1}^K{\mu }_k{h}_k(\bar{\mathit{x}})\le f(\bar{\mathit{x}})$$

• 第一个不等式：下界定义
• 第二个不等式：由于 $\overline{\mathit{x}}$ 满足约束条件，那么 $h_k(\overline{\mathit{x}})=0$，同时 ${\lambda }_j\ge 0$，以及 $g_j(\overline{\mathit{x}})\le 0$。

因此，对于对偶变量有 $ \boldsymbol{\lambda} \geq \mathbf{0}, \Gamma(\boldsymbol{\lambda}, \boldsymbol{\mu}) \leq f\left(\boldsymbol{x}^{*}\right) $。即对于任意可行解，拉格朗日对偶函数小于等于原函数。

如果原问题是凸的，那么有：

$$\underset{\mathit{\lambda },\mathit{\mu }}{max}\mathrm{\Gamma }(\mathit{\lambda },\mathit{\mu })=f\left({\mathit{x}}^{\ast }\right)$$

此时对偶问题的解就是原凸问题的解。否则是严格小于。

SVM 的对偶问题

Soft-SVM 的原问题：

$$\begin{array}{rl}& \underset{\mathit{w},b,\mathit{\xi }}{min}\frac{1}{2}\parallel \mathit{w}{\parallel }_2^2+C\sum _{i=1}^n{\xi }_i\\ \text{s.t. }& 1-{\xi }_i-y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\le 0,-{\xi }_i\le 0,1\le i\le n\end{array}$$

一共有 $2n$ 个不等式约束，$n$ 是样本个数，写出拉格朗日对偶函数，有 3 个原问题变量（类比于 $\mathit{x}$，和 2 个对偶问题变量）：

$$L(\mathit{w},b,\mathit{\alpha },\mathit{\xi },\mathit{\mu })=\frac{1}{2}\parallel \mathit{w}{\parallel }_2^2+C\sum _{i=1}^n{\xi }_i+\sum _{i=1}^n{\alpha }_i(1-{\xi }_i-y_i(\mathit{w}\cdot {\mathit{x}}_i+b))-\sum _{i=1}^n{\mu }_i{\xi }_i$$

同时对偶变量的可行解区域 Dual Feasibility 为：${\alpha }_i\ge 0,{\mu }_i\ge 0,i=1,\dots ,n$。

消去原问题的所有变量，拉格朗日函数对原问题变量求导：

$$\begin{array}{rl}& -\frac{\partial L}{\partial \mathit{w}}=\mathbf{0}\Rightarrow \mathit{w}=\sum _{i=1}^n{\alpha }_i{y}_i{\mathit{x}}_i\\ & -\frac{\partial L}{\partial b}=0\Rightarrow \sum _{i=1}^n{\alpha }_i{y}_i=0\\ & -\frac{\partial L}{\partial {\xi }_i}=0\Rightarrow C={\alpha }_i+{\mu }_i,i=1,\dots ,n\end{array}$$

求完导数之后 $b$ 和 ${\xi }_i$ 都消失了，只有将 $\mathit{w}$ 带入拉格朗日函数：

$$\mathrm{\Gamma }(\mathit{\alpha })=\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)$$

因此 Soft-SVM 的对偶问题就是：

$$\begin{array}{rl}& \underset{\mathit{\alpha }}{max}\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j({\mathit{x}}_i\cdot {\mathit{x}}_j)\\ \text{s.t. }& \sum _{i=1}^n{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C,1\le i\le n\end{array}$$

注意：消去原变量的过程中可能引入新的约束。而 $C={\alpha }_i+{\mu }_i,{\alpha }_i\le 0,{\mu }_i\le 0$ 写在一起就是 $0\le {\alpha }_i\le C$。这个问题就是求 ${\alpha }_i$ 使得对偶问题达到最大值，因为 对偶问题的最大值就是原问题的最小值（严格下界）。凹函数 $\mathrm{\Gamma }$ 只有最大值！对偶变量可能被消掉。

对偶问题的作用：原问题带有仿射变换，而对偶问题只是一个 box 和一个简单一点的仿射约束。原问题有 $n$ 个约束，而对偶问题只有一个约束。因此 Soft-SVM 对偶问题的求解简单了。使用 Quadratic Programm 函数调包吗？这样很慢。对偶问题的目标函数很普通，但是约束很特殊，使用 Sequential Minimal Optimization，SMO 求解：

SMO 是使用迭代的控制变量法，假设任意两个变量 ${\alpha }_i$ 和 ${\alpha }_j$ 未知而其他已知（上一轮迭代确定），那么约束条件也是关于两个未知量的线性方程，用一个表示另一个，带入原函数中，得到一元二次函数，快速求解最值。

利用 $\mathit{w}=\sum _{i=1}^n{\alpha }_i{y}_i{\mathit{x}}_i$ 求出原问题的解。

对偶问题的几何含义

回顾 Soft-SVM 的 KKT 条件的几何解释：

$$\{\begin{array}{l}{\alpha }_i\ge 0,{\mu }_i\ge 0\\ y_i(\mathit{w}\cdot {\mathit{x}}_i+b)-1+{\xi }_i\ge 0\\ {\alpha }_i(y_i(\mathit{w}\cdot {\mathit{x}}_i+b)-1+{\xi }_i)=0\\ {\xi }_i\ge 0\\ {\mu }_i{\xi }_i=0\end{array}$$

• Dual Feasibility：${\alpha }_i\ge 0,{\mu }_i\ge 0$
• Primal Feasibility：$y_i(\mathit{w}\cdot {\mathit{x}}_i+b)-1+{\xi }_i\ge 0$
• Slack Condition：${\alpha }_i(y_i(\mathit{w}\cdot {\mathit{x}}_i+b)-1+{\xi }_i)=0$
• Primal Feasibility：${\xi }_i\ge 0$
• Slack Condition：${\mu }_i{\xi }_i=0$

考察 ${\alpha }_i(y_i(\mathit{w}\cdot {\mathit{x}}_i+b)-1+{\xi }_i)=0$ 的意义：分两种情况：

由 $\mathit{w}=\sum _{i=1}^n{\alpha }_i{y}_i{\mathit{x}}_i$ 可知当 ${\alpha }_i=0$ 意味着第 $i$ 条样本 ${\mathit{x}}_i$ 对最后的解 $\mathit{w}$ 没有影响。那么自然不为零就是有影响，我们将这些有影响的样本称为 支持向量 Support Vector。也就是说，SVM 最后的分类面是由训练样本中那些 ${\alpha }_i\ne 0$ 的样本组成的。而 ${\alpha }_i\ne 0$，根据 Slack Condition 就意味着不在内部，而在边界上，即 $y_i(\mathit{w}\cdot {\mathit{x}}_i+b)-1+{\xi }_i=0$，也就是：

$$y_i(\mathit{w}\cdot {\mathit{x}}_i+b)=1-{\xi }_i\le 1$$

支持向量可能会在夹板里面或夹板上。

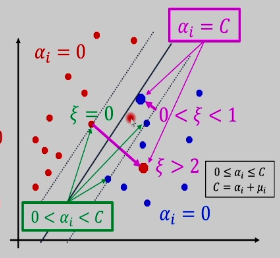
• 当点在上下夹板之外的时候，${\alpha }_i=0$
• 当点在上下夹板之上的时候，${\xi }_i=0$，此时要求 导函数反向，${\mu }_i>0$，因此，$0<{\alpha }_i<C$
• 当点在上下夹板内的时候（可能在内，可能在反例的地方）：$0<{\xi }_i<1,{\xi }_i>2$，因此 ${\mu }_i=0$，所以 ${\alpha }_i=C$

最后的解就是支持向量的线性组合，SV 显然是很少的，那么 SVM 是否能够得到稀疏解呢？稀疏解的好处就是算的快。这件事对现实世界不成立，SVM 的结果一般是不稀疏的（SVM 的一大缺点）。

随机梯度下降

偏好：不带约束的问题。能否对 SVM 用随机梯度下降呢？SGD 能解决 线性约束的二次优化问题 Quadratic Programming with linear constraints 吗？

$$\begin{array}{rl}& \underset{\mathit{x}\in {\mathbb{R}}^d}{min}\frac{1}{2}{\mathit{x}}^T\mathit{Q}\mathit{x}+{\mathit{c}}^T\mathit{x}\\ & \text{s.t. }\mathit{A}\mathit{x}\le \mathit{b}\end{array}$$

写出问题的矩阵形式，直接调包！矩阵运算是经过优化的，比手写 for 循环好很多。

Soft-SVM 的原问题：

$$\begin{array}{rl}& \underset{\mathit{w},b,\mathit{\xi }}{min}\frac{1}{2}\parallel \mathit{w}{\parallel }_2^2+C\sum _{i=1}^n{\xi }_i\\ \text{s.t. }& -y_i\mathit{w}\cdot {\mathit{x}}_i-y_{i}b-{\xi }_i\le -1,-{\xi }_i\le 0,1\le i\le n\end{array}$$

首先自变量有三个，将它写成向量形式：$[\mathit{w},n,\mathit{\xi }{]}^T$，其中 $\mathit{w}$ 同样本的特征维度相同，都是 $d$ 维的。

$$\begin{array}{rl}& \underset{\mathit{w},b,\mathit{\xi }}{min}\frac{1}{2}{\left[\begin{array}{c}\mathit{w}\\ b\\ \mathit{\xi }\end{array}\right]}^T\left[\begin{array}{cc}{\mathit{I}}_d& {\mathbf{0}}_{d,n+1}\\ {\mathbf{0}}_{n+1,d}& {\mathbf{0}}_{n+1,n+1}\end{array}\right]\left[\begin{array}{c}\mathit{w}\\ b\\ \mathit{\xi }\end{array}\right]+\left[\begin{array}{cc}{\mathbf{0}}_{d+1,1}& C{\mathbf{1}}_{n,1}\end{array}\right]\left[\begin{array}{c}\mathit{w}\\ b\\ \mathit{\xi }\end{array}\right]\\ \text{s.t. }& \left[\begin{array}{ccc}-\mathrm{diag}(\mathit{y})& -\mathit{y}& -{\mathit{I}}_n\\ {\mathbf{0}}_{n,d}& {\mathbf{0}}_{n,1}& -{\mathit{I}}_n\end{array}\right]\left[\begin{array}{c}\mathit{w}\\ b\\ \mathit{\xi }\end{array}\right]\le \left[\begin{array}{c}-{\mathbf{1}}_{n,1}\\ {\mathbf{0}}_{n,1}\end{array}\right]\end{array}$$

因此：

$$\begin{array}{rl}& \mathit{x}=\left[\begin{array}{c}\mathit{w}\\ b\\ \mathit{\xi }\end{array}\right],\mathit{Q}=\left[\begin{array}{cc}{\mathit{I}}_d& {\mathbf{0}}_{d,n+1}\\ {\mathbf{0}}_{n+1,d}& {\mathbf{0}}_{n+1,n+1}\end{array}\right],\\ & \mathit{A}=\left[\begin{array}{ccc}-\mathrm{diag}(\mathit{y})& -\mathit{y}& -{\mathit{I}}_n\\ {\mathbf{0}}_{n,d}& {\mathbf{0}}_{n,1}& -{\mathit{I}}_n\end{array}\right],\mathit{b}=\left[\begin{array}{c}-{\mathbf{1}}_{n,1}\\ {\mathbf{0}}_{n,1}\end{array}\right]\end{array}$$

照理来说，对偶问题约束简单，应该更快，但是由于它的优化函数是 $O(n^2)$ 复杂度的。样本条数一多，反而效率满了下来。最后优化的效果是 $O(n^{2.67})$，DeepMind 就是降低矩阵乘法的 $O(n^3)$ 复杂度。而原问题二次项 $\mathit{Q}$ 是一个 $d+n+1$ 维度的，由于它有很多零，它是稀疏的，因此在样本多的情况下还是直接求原问题最快。

结构风险最小化

正则化风险最小化：我们希望机器学习模型符合我们的损失函数范式：宁可要正则项也不要约束项：

引入 合页损失函数 Hinge Loss：

$$\ell (f(\mathit{x}),y)=max\{0,1-yf(\mathit{x})\}$$

• 预测值： $f(\mathit{x})$
• 真实值： $y$
• 对于线性假设： $\ell (f(\mathit{x}),y)=max\{0,1-y(\mathit{w}\cdot \mathit{x}+b)\}$

我们可以证明带约束的 SVM 等价于下面的不带约束的 SVM，这也是 SVM 走过的最大的弯路。首先回到 Soft-SVM 最初始形式：

$$\begin{array}{rl}& \underset{\mathit{w},b,\mathit{\xi }}{min}\frac{1}{2}\parallel \mathit{w}{\parallel }_2^2+C\sum _{i=1}^n{\xi }_i\\ \text{s.t. }& y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\ge 1-{\xi }_i,{\xi }_i\ge 0,1\le i\le n\end{array}$$

将约束消去就是将 ${\xi }_i$ 消去，这个问题是关于 ${\xi }_i$ 的线性约束线性优化问题。为了使目标函数尽可能小，那么要求 ${\xi }_i$ 的最小值。

$${\xi }_i\ge 1-y_i(\mathit{w}\cdot {\mathit{x}}_i+b);{\xi }_i\ge 0$$

分类讨论：如果 $1-y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\le 0$，那么 ${\xi }_i$ 的最小值就是 0，否则 ${\xi }_i$ 的最小值就是 $1-y_i(\mathit{w}\cdot {\mathit{x}}_i+b)$。因此：

$${\xi }_i=max\{0,1-y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\}$$

${\xi }_i$ 就对应这样一个分段函数，所谓的合页损失函数。

机器学习的四大损失函数：

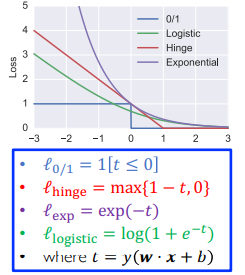
• 01 损失函数：如果 score 错了，那么损失为 1，否则损失为 0
• 合页损失函数：当 $t\ge 1$ 时就是在夹板外，没有损失，当 $t\le 1$ 时，有损失，按照线性惩罚
• 指数损失函数：Boosting
• 逻辑斯蒂损失函数：Logistic Regression

那直接将 ${\xi }_i$ 的最小值带入目标函数中去，不就是求到了目标函数的最小值吗？因为对于固定的参数 $\mathit{w},b$ 而言，${\xi }_i$ 就是所谓的变量。因此目标函数的最小值为（将 ${\xi }_i$ 替换为最优解）：

$$\underset{\mathit{w},b}{min}\frac{1}{2}\parallel \mathit{w}{\parallel }_2^2+\frac{C}{n}\sum _{i=1}^{n}max\{0,1-y_i(\mathit{w}\cdot {\mathit{x}}_i+b)\}$$

GD 方法直接求解不可行，因为 Hinge Loss 有一个点不可导。采用次梯度，令 $t=1$ 处的导数为 0 即可。次梯度为：

$${\mathit{g}}_i^t=\{\begin{array}{ll}{\mathit{w}}^t& \text{ if }{y}_i({\mathit{w}}^t\cdot {\mathit{x}}_i+b)\ge 1\\ {\mathit{w}}^t-C{y}_i{\mathit{x}}_i& \text{ otherwise }\end{array}$$

参数更新方程 ${\mathit{w}}^{t+1}\leftarrow {\mathit{w}}^t-\eta {\mathit{g}}^t$，这个算法依然是 $1/\sqrt{T}$ 的收敛速度。

如果目标函数是强凸的（二次项是强凸的，合页损失不是强凸的，加起来就是强凸的），有一个更快的方法。

输出：#TODO 为啥要求平均值。

$$\bar{\mathit{w}}=\frac{1}{T}\sum _{t=1}^T{\mathit{w}}^t$$

支持向量回归

Support Vector Regression：SVR，不要推导对偶问题，这个直接用 SGD 求就行（换了个损失函数）。