第三章 线性模型

回顾一下机器学习的基本框架：

• 任务是求出未知的目标函数：$f:\mathcal{X}\to \mathcal{Y}$
• 给出一组训练数据 $({\mathit{x}}_1,y_1),...,({\mathit{x}}_N,y_N)$
• 选定一个假设空间 $\mathcal{H}$：具备正则性
• 通过某个学习算法 $\mathcal{A}$ 从假设空间中找到最优的假设函数 $h$
• 目标函数有时也叫最优分类器 Optimal Classifier
• 目标函数在数据集上的错误率称为贝叶斯错误率 Bayes Error

显然，线性空间就是一个具备正则性的假设空间。接下来我们介绍线性模型的学习算法。

线性回归基本概念

用电量预测

先看一个简单的例子：用电量预测。我们需要预测夏季的用电量，已知信息为如下表格：

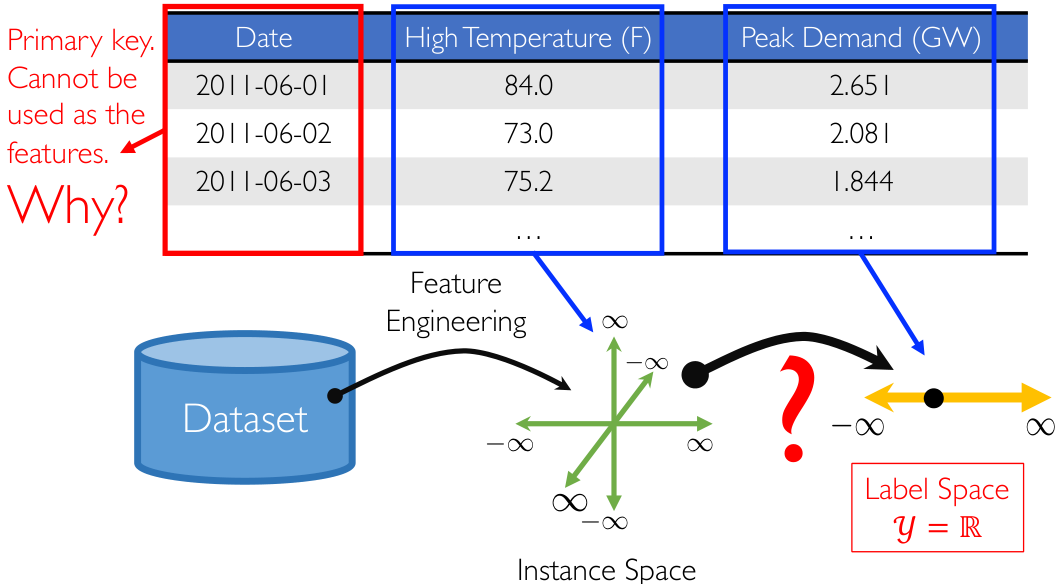
注意到：主键 Primary key 是不能作为特征的。因此我们可以对表格数据做特征提取，将每日最高温度作为特征，在特征空间/实例空间 Instance Space 中画出来，显然这是一个 ${\mathbb{R}}^1$ 的空间；同时将高峰用电量作为输出/响应值，在标签空间 Label Space 中画出来，标签空间一般都是标量 $\mathbb{R}$。机器学习的目标就是找到从实例空间到标签空间的一个最佳映射。

这个映射应该是一个什么类型的函数呢？一般不会瞎猜，而是对数据做探索式数据分析 Exploratory Data Analysis，EDA 的前置步骤，通常就是对数据做可视化处理。

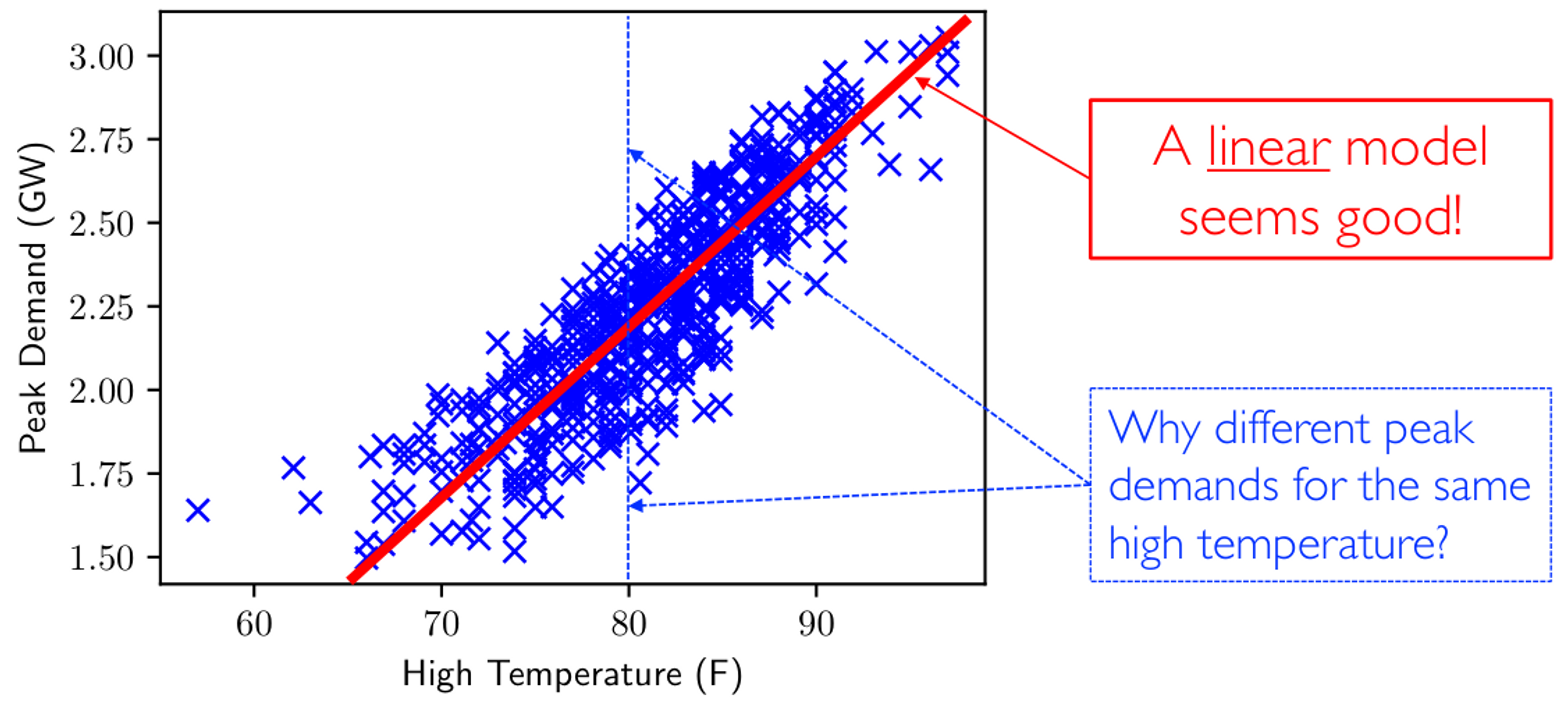
我们发现线性模型看上去拟合程度不错，但是仍然存在一些问题：为什么有些相同的温度对应了不同的用电峰值呢？这是一种不正常的现象。模型不完美的原因可能是：用电峰值不仅仅和温度有关，还和其他特征有关。EDA 阶段可以帮助我们找到假设空间，发现特征之间的强相关性……

线性假设空间

由于输入数据 $\mathit{x}$ 是一个 $d$ 维向量，因此我们可以认为假设空间是 $d$ 维空间中所有线性超平面。由线性代数知识可知，这种线性超平面可以表达为以下形式：

$$h(\mathit{x})=w_0+\sum _{j=1}^d{w}_j{x}_j=\sum _{j=0}^d{w}_j{x}_j=\mathit{w}\cdot \mathit{x}$$

其中，$w_0$ 一般称为截距，同时扩充 $d$ 维向量为：

$$\mathit{x}=\left(\begin{array}{c}1\\ x_1\\ ...\\ x_d\end{array}\right)\in {\mathbb{R}}^{d+1}$$

同时 $\mathit{w}$ 是这个超平面的法向量 normal vector。因为令 $h(\mathit{x})=\mathit{w}\cdot \mathit{x}=0$ 就是一个超平面，而这个超平面上的点 $\mathit{x}$ 同时也满足和参数向量 $\mathit{w}$ 的内积为 0，因此 $\mathit{w}$ 的几何意义就是线性超平面的法向量，垂直于超平面中的所有向量，同时它也与线性超平面一一对应。

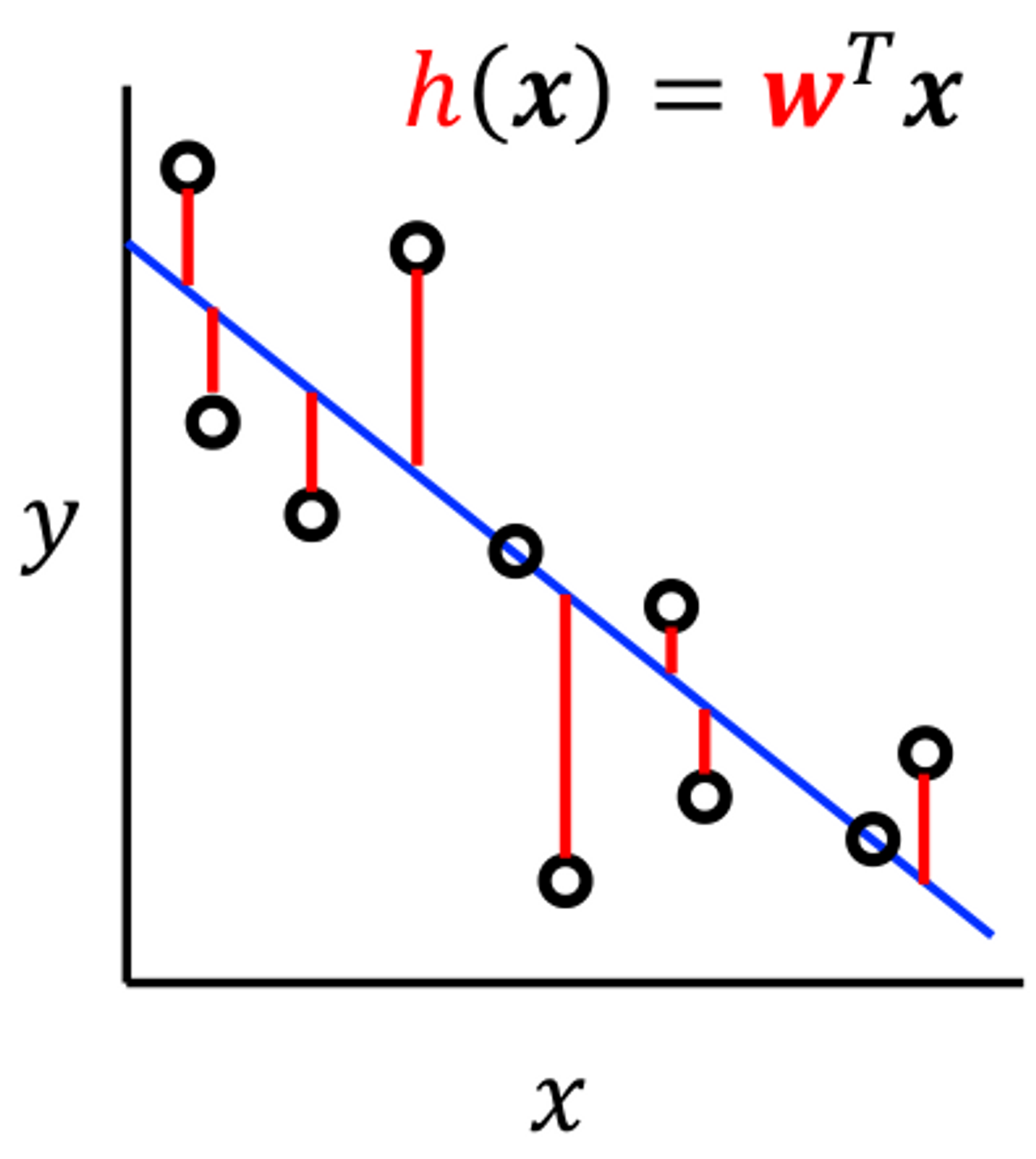
损失函数

这是一个回归问题，采用均方误差损失 squared loss/L2 loss 来计算训练集上的误差：

$$\widehat{ϵ}(h)=\sum _{i=1}^n(h({\mathit{x}}_i)-y_i{)}^2$$

我们一般将 $\hat{}$ 称为经验样本值，表示它是在训练样本集上算出来的，这是一个惯例 convention。如果是一个分布的期望值，那么没有这个符号。

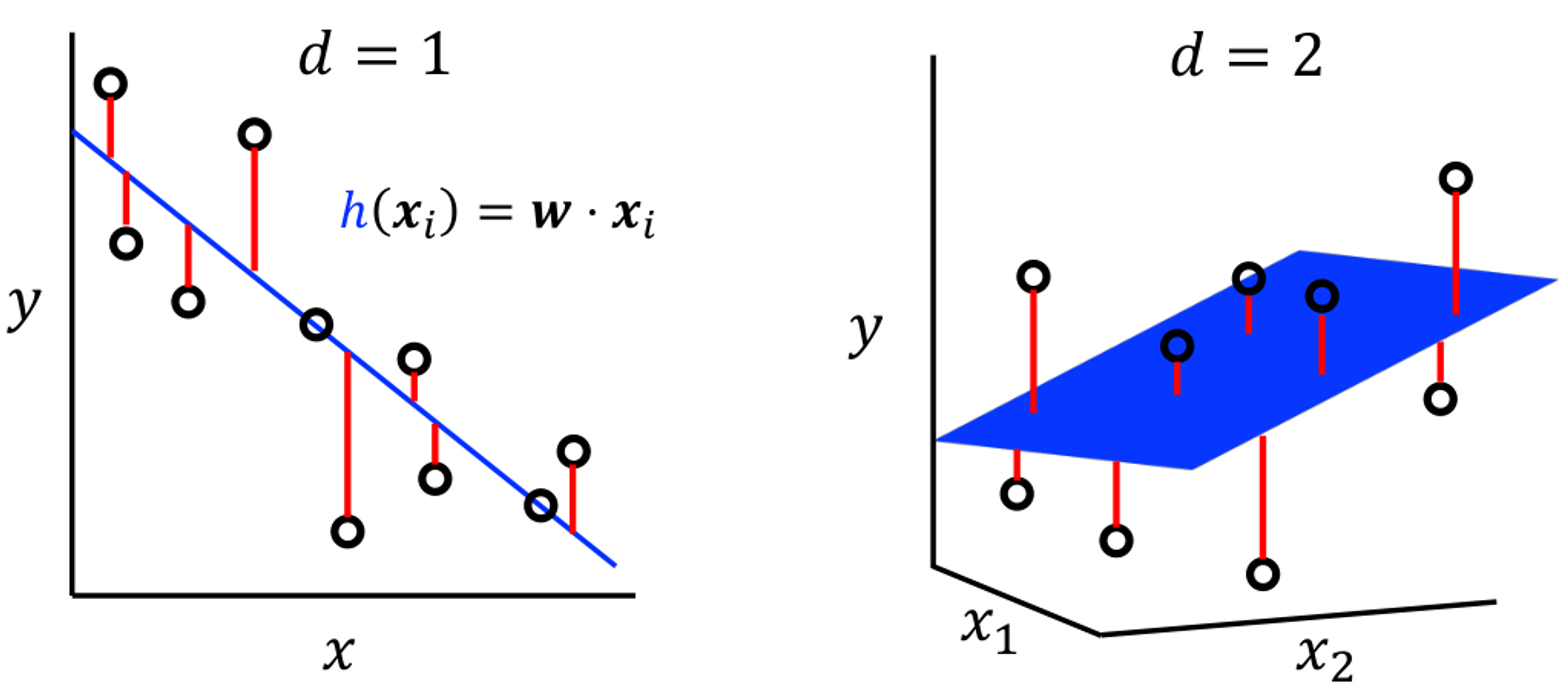
我们的目标就是最小化损失函数之和，也就是最小化训练误差，这就是我们的优化目标：找到一个最优超平面（对应的法向量 $\mathit{w}$），使得训练误差达到最小：

$$\underset{\mathit{w}}{\text{min}}\sum _{i=1}^n(h_{\mathit{w}}({\mathit{x}}_i)-y_i{)}^2$$

解析解

我们将线性回归的训练误差写成矩阵形式：

$$\widehat{ϵ}(\mathit{w})=\sum _{i=1}^n{({\mathit{w}}^{\mathrm{T}}{\mathit{x}}_i-y_i)}^2=\parallel \mathit{X}\mathit{w}-\mathit{y}{\parallel }^2$$

此时引入了两个矩阵，分别是数据/设计矩阵 $\mathit{X}\in {\mathbb{R}}^{n\times (d+1)}$ 和标签矩阵 $\mathit{y}\in {\mathbb{R}}^{n\times 1}$：

$$\mathit{X}=\left[\begin{array}{c}-{\mathit{x}}_1^{\mathrm{T}}-\\ -{\mathit{x}}_2^{\mathrm{T}}-\\ ⋮\\ -{\mathit{x}}_n^{\mathrm{T}}-\end{array}\right]=\left[\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_{1d}\\ 1& x_{21}& x_{22}& \cdots & x_{2d}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_{n1}& x_{n2}& \cdots & x_{nd}\end{array}\right],\mathit{y}=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right]$$

因为 $\mathit{X}\mathit{w}-\mathit{y}$ 是一个 $n$ 维向量，因此它的范数平方就是每一维数据平方和。不熟悉矩阵运算的可以去看看这本书：https://www.math.uwaterloo.ca/~hwolkowi/matrixcookbook.pdf

接下来就是考察 $\widehat{ϵ}(\mathit{w})$ 关于向量 $\mathit{w}$ 的导数，并令其为 0 求出最优的 ${\mathit{w}}^{\ast }$：

$$\begin{array}{rl}& {\mathrm{\nabla }}_{\mathit{w}}\widehat{ϵ}(\mathit{w})=2{\mathit{X}}^{\mathrm{T}}(\mathit{X}\mathit{w}-\mathit{y})=\mathbf{0}\\ \Rightarrow & {\mathit{X}}^{\mathrm{T}}\mathit{X}\mathit{w}={\mathit{X}}^{\mathrm{T}}\mathit{y}\\ \Rightarrow & {\mathit{w}}^{\ast }={\left({\mathit{X}}^{\mathrm{T}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathrm{T}}\mathit{y}\end{array}$$

我们将最后的式子称为正规方程 Normal Equation，我们可以发现最后的式子复杂性太高：矩阵乘法的复杂性为 $\mathcal{O}(d^2)$，求逆矩阵的复杂性为 $\mathcal{O}(d^3)$，因此最后的计算复杂性为 $\mathcal{O}[d^2(d+n)]$，非常大，因为现实中 $d\approx 50$，因此这个算法不会被使用。

优化方法

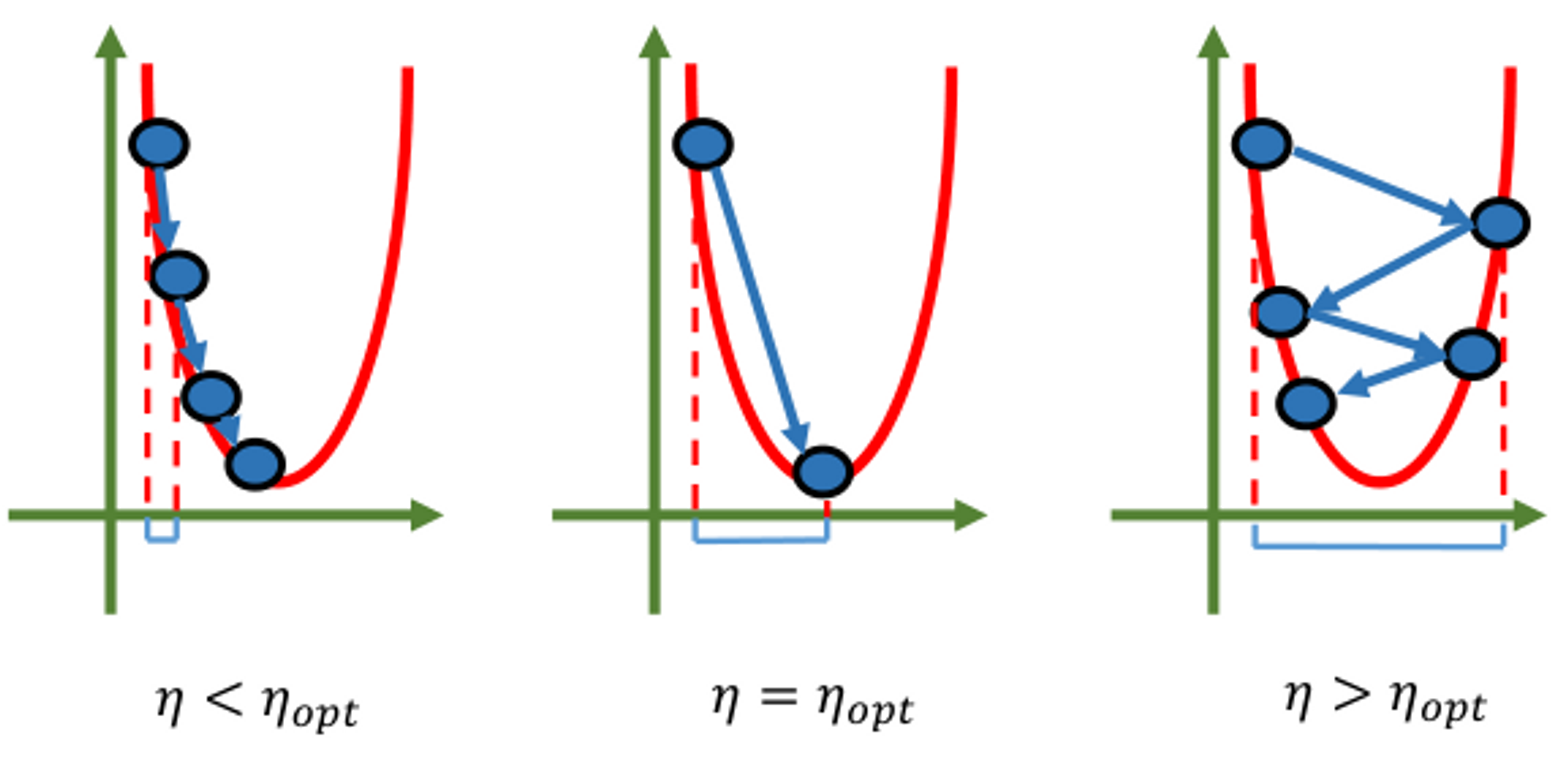
由于正规方程的解析解计算起来复杂度太高，同时实际应用中有很多方程是很难求得解析解的。因此我们考虑一种通用的优化方法——梯度下降法 Gradient Descent，GD，它适用于绝大多数可微的损失函数。沿着梯度方向，函数值下降最快（梯度的定义：最大的方向导数，即沿着该方向函数的变化率最大）。

梯度

首先对向量函数求每一维的偏导数，然后将其串成一个向量，就是梯度向量：

$$g_j={\mathrm{\nabla }}_{w_j}J(\mathit{w})=\frac{\partial J(\mathit{w})}{\partial w_j},\mathit{g}={\mathrm{\nabla }}_{\mathit{w}}J(\mathit{w})$$

对向量函数 $J(\mathit{w})$ 作一阶泰勒展开：

$$J(\mathit{w})=J({\mathit{w}}_0)+(\mathit{w}-{\mathit{w}}_0{)}^{\mathrm{T}}\mathit{g}+\cdots$$

沿着梯度方向走一小步 $\eta$，就有：

$$J(\mathit{w}-\eta \mathit{g})\approx J(\mathit{w})-\eta {\mathit{g}}^{\mathrm{T}}\mathit{g}$$

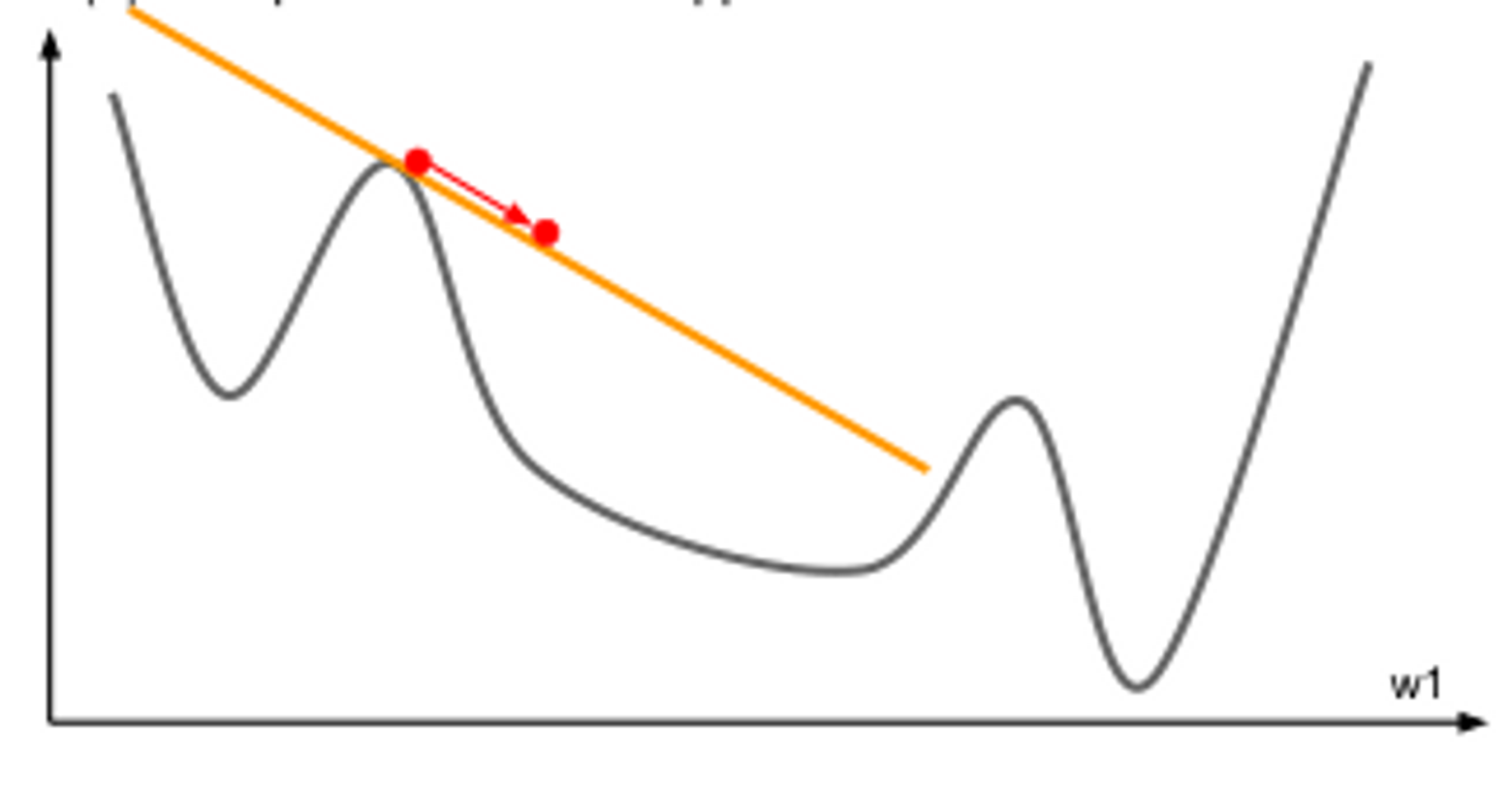
此时显然有 $-\eta {\mathit{g}}^{\mathrm{T}}\mathit{g}\le 0$，（因为 ${\mathit{g}}^T\mathit{g}$ 就是模长的平方，是一个正数）因此我们减小了原函数值的大小，重复上述步骤就得到了梯度下降算法，直到求到极小值为止。这种方法也被称为优化问题的一阶方法，主要运用了一阶泰勒展开；而牛顿法也被称为二阶方法，这两种方法构成了优化问题的主要解决方法。

梯度下降算法能够找到凸函数的最小值。

梯度下降算法

通用优化算法：迭代式程序

• 对于每一轮迭代 $t(\le T)$
  • 当参数向量 ${\mathit{w}}^t$ 还没有收敛，即对应的函数值还不是极值
  • 更新 ${\mathit{w}}^{t+1}\leftarrow {\mathit{w}}^t-\eta {\mathrm{\nabla }}_{\mathit{w}}\widehat{ϵ}(\mathit{w}){|}_{\mathit{w}={\mathit{w}}^t}$
• 把 $\eta$ 称为学习率 learning rate，是一个很重要的超参数（在深度学习中更加重要）
• 理论表明，在凸函数下，收敛速率为 $\mathcal{O}(1\sqrt{T})$，当迭代 $t$ 次，误差下降为初始值的 $1/\sqrt{t}$
• 在线性回归（是凸函数）中，只需要算出梯度即可：
  • 更新 ${\mathit{w}}^{t+1}\leftarrow {\mathit{w}}^t-2\eta {\mathit{X}}^{\mathrm{T}}(\mathit{X}{\mathit{w}}^t-\mathit{y})$
  • 算法的复杂度主要来自于梯度的计算：$\mathcal{O}(dnT)$

矩阵乘法中，小的矩阵要优先乘，即先算后面的向量。

随机梯度下降

我们发现，每一步都要计算当前点的梯度 $2{\mathit{X}}^{\mathrm{T}}(\mathit{X}{\mathit{w}}^t-\mathit{y})$，但是却只走了一小步 $\eta$，因此有些浪费。于是我们可以采用如下的随机梯度下降 Stochastic Gradient Descent，SGD。

• 对于每一轮迭代 $t(\le T)$

  • 随机从数据点中选择一小批数据 minibatch：${({\mathit{x}}_i,y_i)}_{i=1}^m,m\ll n$

  • 计算这一小批数据的经验误差：

    $$J^t({\mathit{w}}^t)=\frac{1}{m}\sum _{i=1}^m\ell ({\mathit{w}}^t;{\mathit{x}}_i,y_i)$$

  • 计算这一小批数据的梯度：${\mathrm{\Delta }}^t={\mathrm{\nabla }}_{\mathit{w}}{J}^t({\mathit{w}}^t)$

  • 更新参数：${\mathit{w}}^{t+1}={\mathit{w}}^t-\eta {\mathrm{\Delta }}^t$

• 对于线性回归就是：
  • 更新参数：${\mathit{w}}^{t+1}\leftarrow {\mathit{w}}^t-2\eta {\mathit{X}}_m^{\mathrm{T}}({\mathit{X}}_m{\mathit{w}}^t-\mathit{y})$
  • 计算复杂度：$\mathcal{O}(dmT),m\ll n$
• 深度学习基本都使用 SGD 方法，因为它是最快的，只与维度和迭代次数成正比
• 理论表明，在凸函数下，收敛速率依然是 $\mathcal{O}(1\sqrt{T})$

统计视角

参数化模型中的似然函数

在线性回归中，为什么要用均方误差作为损失函数呢？我们从统计视角来回答这个问题。

假设我们有一个以 $\theta$ 作为参数的参数化概率模型 $\{p(\mathit{z};\theta )|\theta \in \mathrm{\Theta }\}$，一组训练数据是以某个概率模型独立同分布生成的：$\mathcal{D}=({\mathit{z}}_1,\cdots ,{\mathit{z}}_n)$。定义一个似然函数，刻画了参数 $\theta$ 对样本集 $\mathcal{D}$ 的描述能力，即似然函数越大，表示描述能力越强，也就是这个参数化模型越接近样本真实的概率分布：

$$p(\mathcal{D};\hat{\theta })\triangleq \prod _{i=1}^{n}p({\mathit{z}}_i;\hat{\theta })$$

也就是运用了独立同分布概率的乘法原理。为了避免数字过小导致下溢出，机器学习中往往使用对数似然函数 log-likelihood：

$$\log p(\mathcal{D};\theta )\triangleq \sum _{i=1}^n\log p({\mathit{z}}_i;\theta )$$

最大似然估计

最大似然估计 Maximum Likelihood Estimator，MLE 方法就是找到一组参数 $\theta$，使得似然函数达到最大值，这也是一个优化问题，可以用 SGD 方法求解：

$$\hat{\theta }\in \underset{\theta \in \mathrm{\Theta }}{\text{argmax}}\log p(\mathcal{D};\theta )\Rightarrow \hat{\theta }\in \underset{\theta \in \mathrm{\Theta }}{\text{argmax}}\sum _{i=1}^n\log p({\mathit{z}}_i;\theta )$$

同时，在特定的分布假设下，一个最大似然估计过程会对应着机器学习中的一个损失函数。

判别模型

在监督学习模型中，我们将训练数据集 $\mathcal{D}=\{({\mathit{x}}_1,y_1),\cdots ,({\mathit{x}}_n,y_n)\}$ 中的 $({\mathit{x}}_i,y_i)$ 看作一条数据 ${\mathit{z}}_i$，因此独立同分布的 ${\mathit{z}}_i$ 可以看作是通过某个概率分布模型 $p(\mathit{x},y$) 生成的，运用条件概率公式：

$$p(\mathcal{D}\mathcal{;}\hat{\theta })\triangleq \prod _{\mathcal{i}\mathcal{=}\mathcal{1}}^{\mathcal{n}}\mathcal{p}({\mathcal{x}}_{\mathcal{i}}\mathcal{,}{\mathcal{y}}_{\mathcal{i}}\mathcal{;}\hat{\theta })\mathcal{=}\prod _{\mathcal{i}\mathcal{=}\mathcal{1}}^{\mathcal{n}}\mathcal{p}({\mathcal{y}}_{\mathcal{i}}|{\mathcal{x}}_{\mathcal{i}}\mathcal{;}\hat{\theta })\mathcal{p}\mathcal{(}{\mathcal{x}}_{\mathcal{i}}\mathcal{)}$$

其中 $p({\mathit{x}}_i)$ 是 ${\mathit{x}}_i$ 数据自身的边缘分布，而这个是非常复杂的，建模数据的边缘分布问题被称作生成模型，本门课程不讲。我们引入的是判别模型 discriminative model，指的是直接建模了 $\mathit{x}$ 与 $y$ 之间的关系而不建模其他关系的模型（机器学习的所有模型几乎都是判别模型，即不关心 $\mathit{x}$ 自身的分布情况，只关心输入 $\mathit{x}$ 与输出 $y$ 之间的关系）。因此我们做了一个非常强的假设，即认为数据自身的分布服从经验分布：

$$p({\mathit{x}}_i)=\frac{1}{n}$$

即对于 $n$ 条数据，有数据点的地方概率为 $1/n$，没有数据点的地方概率为 0（但实际上也许是我们没有采样到罢了，因此我们这样做机器学习的时候，需要数据量要尽量大）而如果某个机器学习模型不成功，那么有可能是数据自身的分布对结果影响很大，而我们在做判别模型的时候没有考虑。

但是之后的学习理论课会告诉我们，即使在这么强的假设条件下，判别模型依然可以给出期望误差的一个估计，也就是说勉强能用！

将上述经验分布式代入条件概率公式得到：

$$\prod _{i=1}^{n}p(y_i|{\mathit{x}}_i;\hat{\theta })p({\mathit{x}}_i)=\prod _{i=1}^n\frac{1}{n}p(y_i|{\mathit{x}}_i;\hat{\theta })\propto \prod _{i=1}^{n}p(y_i|{\mathit{x}}_i;\hat{\theta })$$

因此对于判别模型，我们可以找到一组参数 $\theta$ 使得上述式子达到最大，一般称其为似然函数/对数似然函数：

$$\begin{array}{rl}p(\mathcal{D};\theta )& \triangleq \prod _{i=1}^{n}p(y_i|{\mathit{x}}_i;\theta )\\ \log p(\mathcal{D};\theta )& =\sum _{i=1}^n\log p(y_i|{\mathit{x}}_i;\theta )\end{array}$$

那么判别模型的极大似然估计就是（拿掉了边缘分布）：

$$\text{widehat{theta}=argmaxlimits\_{theta}sum\_{i=1}^{n}log p(y\_i|boldsymbol{x}\_i;theta)}$$

高斯噪声假设

高斯噪声假设是线性回归模型的基本假设。我们认为标签值 $y$ 与线性模型 ${\mathit{w}}^{\mathrm{T}}\mathit{x}$ 之间差一个高斯噪声 $e$，其满足均值是 0，方差为 $\sigma$ 的高斯分布，也叫高斯白噪声：

$$e\sim \mathcal{N}\mathcal{(}\mathcal{0}\mathcal{,}{\sigma }^{\mathcal{2}}\mathcal{)}$$

也就是 $y={\mathit{w}}^{\mathrm{T}}\mathit{x}+e$，因此 $y$ 服从的分布为：

$$y\sim \mathcal{N}\mathcal{(}{\mathcal{w}}^{\mathrm{T}}\mathcal{x}\mathcal{,}{\sigma }^{\mathcal{2}}\mathcal{)}$$

因此输出标签的期望值为：

$$\mathbb{E}(y|\mathit{x};\mathit{w},{\sigma }^2)={\mathit{w}}^{\mathrm{T}}\mathit{x}$$

我们将这种期望 $\mathbb{E}(y|\mathit{x})$，也就是条件概率 $p(y|\mathit{x})$ 的期望叫做回归方程 Regression Function。在线性回归中，我们使用线性方程对回归方程进行逼近，因此称其为线性回归。

同时我们还有 $n$ 条独立同分布的样本数据 $\mathcal{D}=\{({\mathit{x}}_1,y_1),\cdots ,({\mathit{x}}_n,y_n)\}$，我们通过求取极大似然估计就可以得到该参数化模型下的最优参数 ${\mathit{w}}^{\ast }$。

假设条件概率分布符合高斯分布：$y_i|{\mathit{x}}_i;{\mathit{w}}_i\sim \mathcal{N}({\mathit{w}}^T{\mathit{x}}_i,{\sigma }^2)$，因此有两个参数 $\theta =\{\mathit{w},\sigma \}$。对于每一个数据点 $({\mathit{x}}_i,y_i)$，有：

$$p(y_i|{\mathit{x}}_i;\mathit{w},\sigma )={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}\exp \{-{\displaystyle \frac{1}{2{\sigma }^2}}{(y_i-{\mathit{w}}^{\mathrm{T}}{\mathit{x}}_i)}^2\}$$

那么在全体训练集 ${\mathcal{D}}_{\mathcal{n}}$ 上的对数似然函数为：

$$\begin{array}{rl}\log p({\mathcal{D}}_n;\mathit{w},\sigma )& =\sum _{i=1}^n\log p(y_i|{\mathit{x}}_i;\mathit{w},\sigma )\\ & =\frac{n}{2}\log \frac{1}{2\pi {\sigma }^2}-\frac{1}{2{\sigma }^2}\sum _{i=1}^n{(y_i-{\mathit{w}}^{\mathrm{T}}{\mathit{x}}_i)}^2\end{array}$$

做最大似然估计：

$$\begin{array}{rl}{\mathit{w}}^{\ast }& ={\text{argmax}}_{\mathit{w}}\frac{n}{2}\log \frac{1}{2\pi {\sigma }^2}-\frac{1}{2{\sigma }^2}\sum _{i=1}^n{(y_i-{\mathit{w}}^{\mathrm{T}}{\mathit{x}}_i)}^2\\ & ={\text{argmax}}_{\mathit{w}}-\frac{1}{2{\sigma }^2}\sum _{i=1}^n{(y_i-{\mathit{w}}^{\mathrm{T}}{\mathit{x}}_i)}^2\\ & ={\text{argmin}}_{\mathit{w}}\sum _{i=1}^n{(y_i-{\mathit{w}}^{\mathrm{T}}{\mathit{x}}_i)}^2\end{array}$$

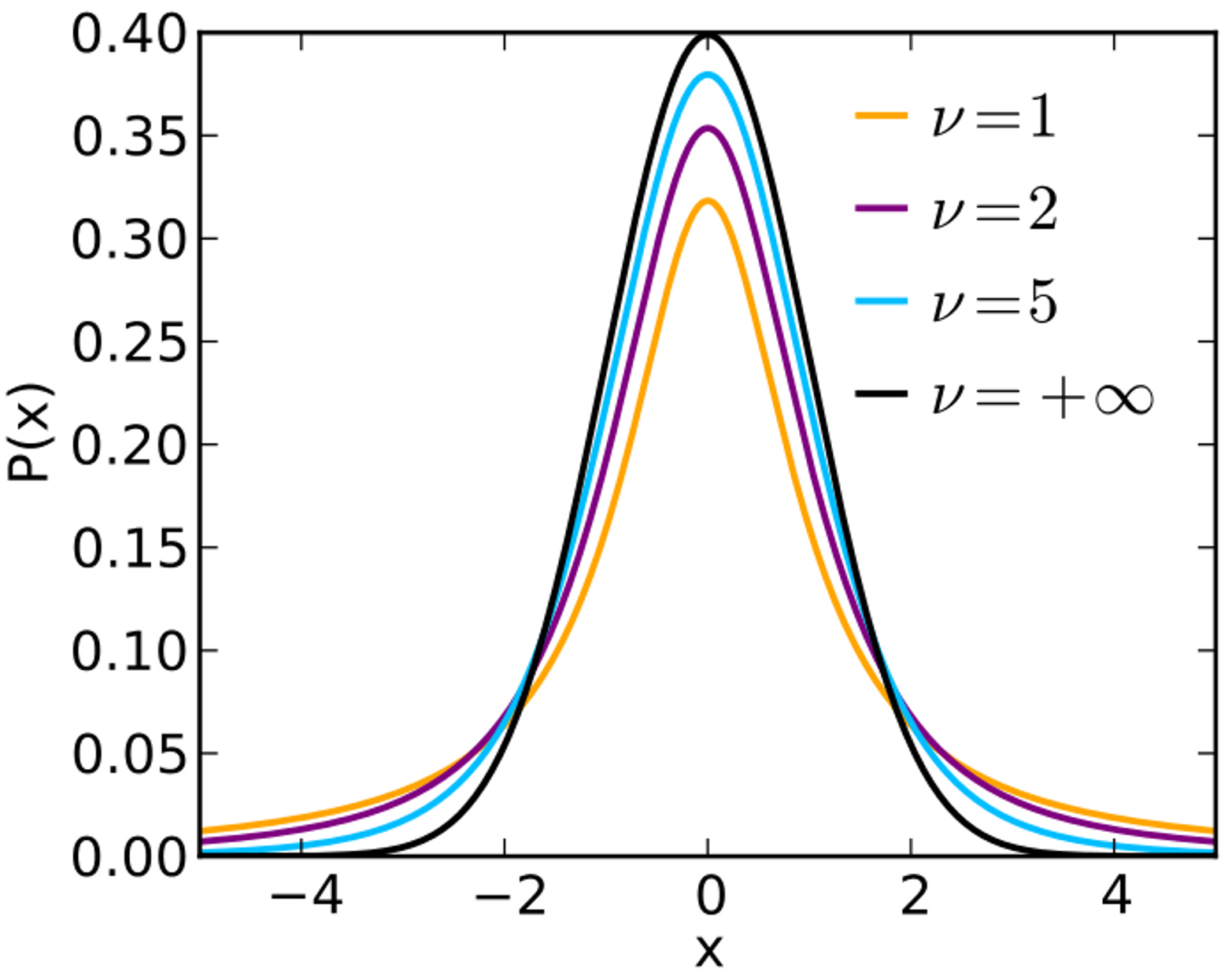
这就说明：采用均方误差损失的线性回归等价于高斯噪声假设下的线性模型的最大似然估计。那么如果噪声模型不符合高斯分布，那么就不能用均方误差损失作为损失函数！例如长尾分布 t 分布就有自己的损失函数/待优化的目标函数。t 分布主要用于对噪声本身进行建模。

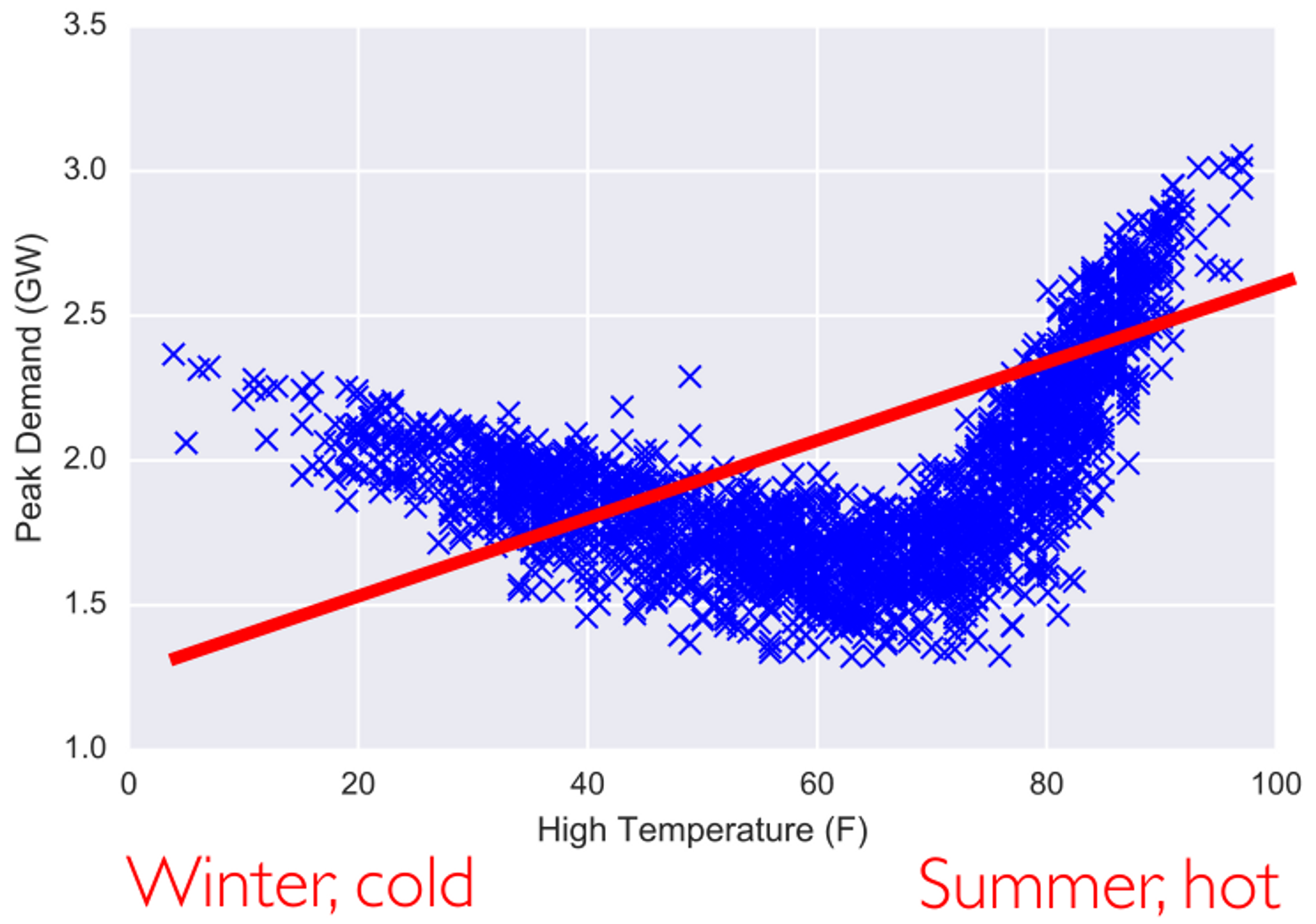
非线性化

首先，我们通过 EDA 模型发现这是一个非线性模型，如果此时还用线性模型，就会出现欠拟合：

基函数

基 Basis 的概念是从线性空间中引申而来的。特征映射：将特征向量 $\mathit{x}=(x_1,\cdots ,x_d)\in \mathcal{X}$ 通过某种映射关系 $\mathrm{\Phi }$ 转化为新的特征向量 $\mathit{z}=(z_1,\cdots ,z_{\tilde{d}})\in \mathcal{Z}$，记作：

$$\mathit{z}=\mathrm{\Phi }(\mathit{x})$$

线性代数中就是矩阵变换，但矩阵是一个线性变换，我们要做的是非线性映射：即每个 $z_j={\varphi }_j(\mathit{x})$ 都需要 ${\varphi }_j$ 是一个非线性变换。我们将 $\{{\varphi }_j{\}}_{1\le j\le \tilde{d}}$ 称为基函数，输入为向量，输出为标量。

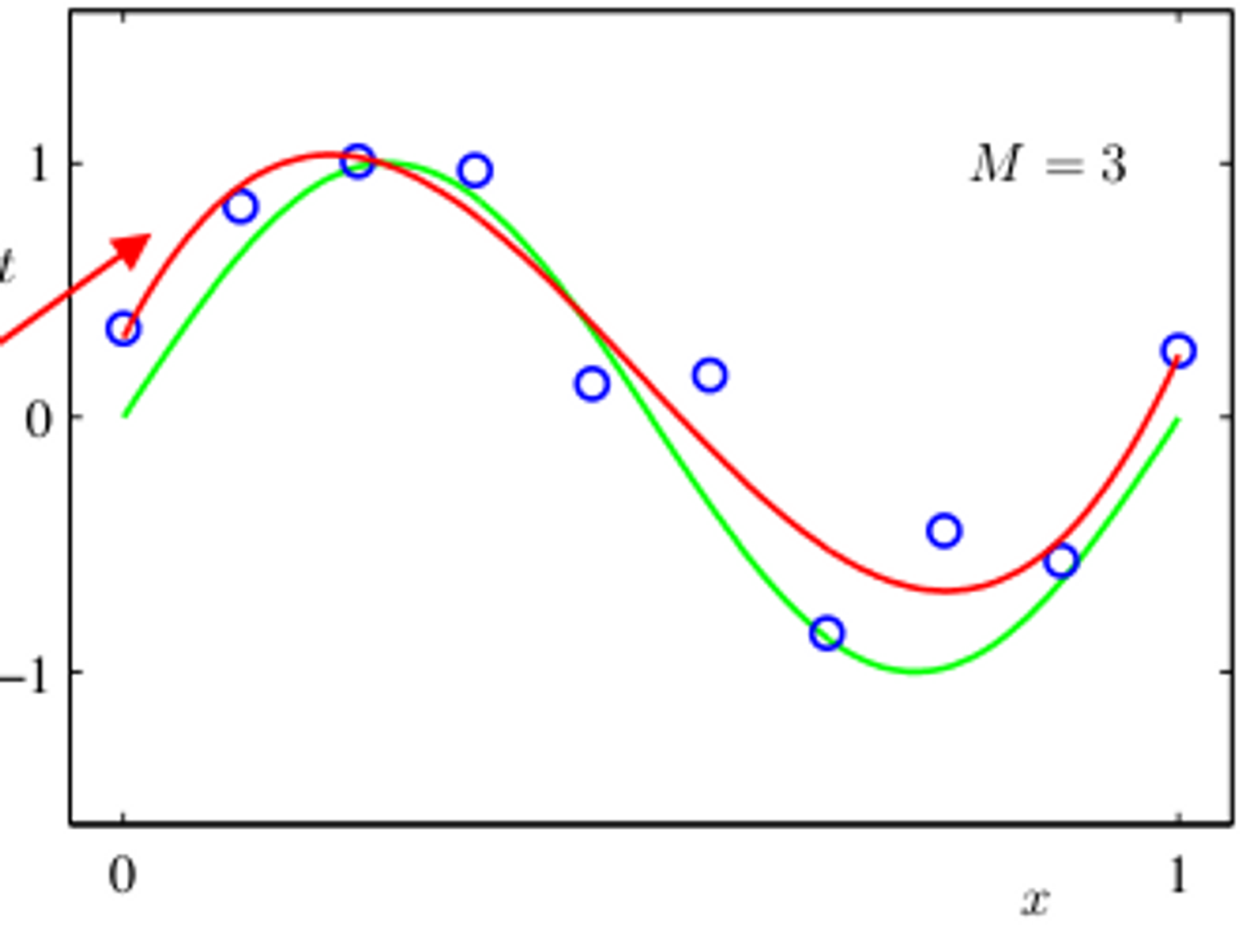
如图所示是一个三次函数，显然不能用线性模型拟合，但如果我们构造如下多项式基函数：

$$\mathit{z}=(1,x,x^2,x^3)$$

一共有 4 个基函数，它们将 1 维特征向量映射成了 4 维特征向量，以 $\mathit{z}$ 为输入做线性拟合就可以得到图中红色曲线，即 $y=w_0+w_{1}x+w_2{x}^2+w_3{x}^3$。如果将 2 维特征向量进行映射：

$$\mathit{z}=(1,x_1,x_2,x_1^2,x_2^2,x_1{x}_2)$$

问题在于：基函数该如何构造？不仅是高次多项式，甚至 $e^x$ 也可以作为基函数。而如果 $\mathit{x}\in {\mathbb{R}}^d$ 是一个高维向量，我们还要考虑不同维度之间的关系。这种从原始数据中提取更好特征的过程就是特征工程。我们可以通过领域知识，可以通过数据可视化方法等等来构造基函数。

机器学习中我们常使用径向基函数 Radial Basis Functions，RBF：

$${\varphi }_j(\mathit{x})=\{\exp (-{\displaystyle \frac{||\mathit{x}-{\mathit{\mu }}_j|{|}_2^2}{2{\sigma }^2}}):j=1,\dots ,\tilde{d}\}$$

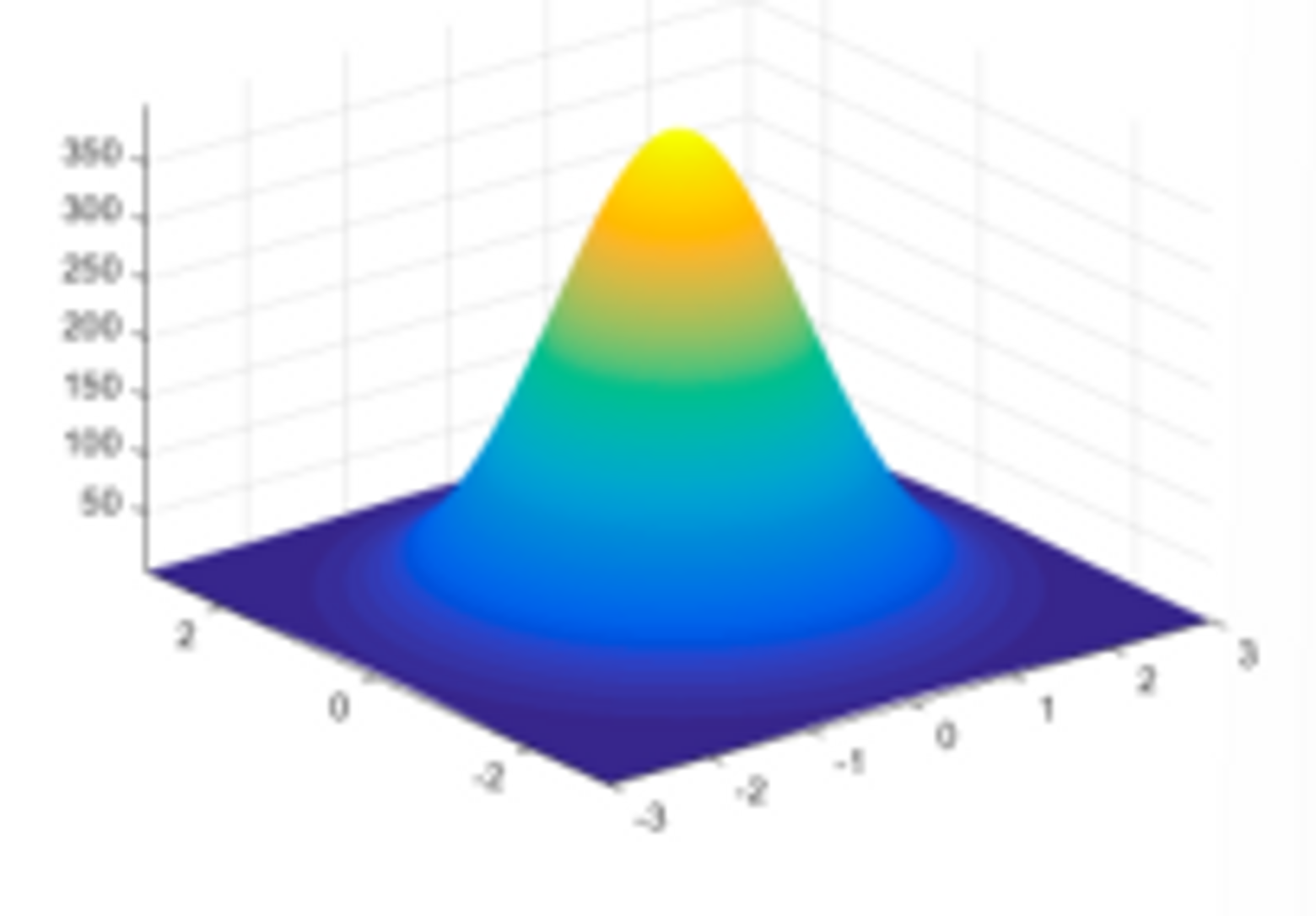
也称为高斯核函数。它将每一个数据 $\mathit{x}$ 映射为 $\tilde{d}$ 维数据，每一维刻画了它和每一维均值 ${\mathit{\mu }}_j$ 之间的距离。在概率中，我们通常认为多个高斯分布的混合可以表达任意复杂的分布。这个基函数的含义就是用 $\tilde{d}$ 个高斯分布混合后表达这个数据集，以及每一个数据具体在什么位置上。

非线性化映射

非线性映射之后，我们会在新的特征空间 $\mathcal{Z}$ 上定义一个线性模型：

$$h(\mathit{x})=\tilde{\mathit{w}}\cdot \mathit{z}=\tilde{\mathit{w}}\cdot \mathrm{\Phi }(\mathit{x})=\sum _{j=1}^{\tilde{d}}{\tilde{w}}_j{\varphi }_j(\mathit{x})$$

在整个式子中 ${\varphi }_j(\mathit{x})$ 是已知的，只有 ${\tilde{w}}_j$ 是未知的，同时这个模型也是关于 ${\tilde{w}}_j$ 是线性的，因此也叫做线性模型（尽管它关于 $\mathit{x}$ 是非线性的）。线性回归使用了多项式作为基函数后就成为了多项式回归，可以拟合任何多项式。再根据泰勒展开，可以拟合任意可微的连续函数。

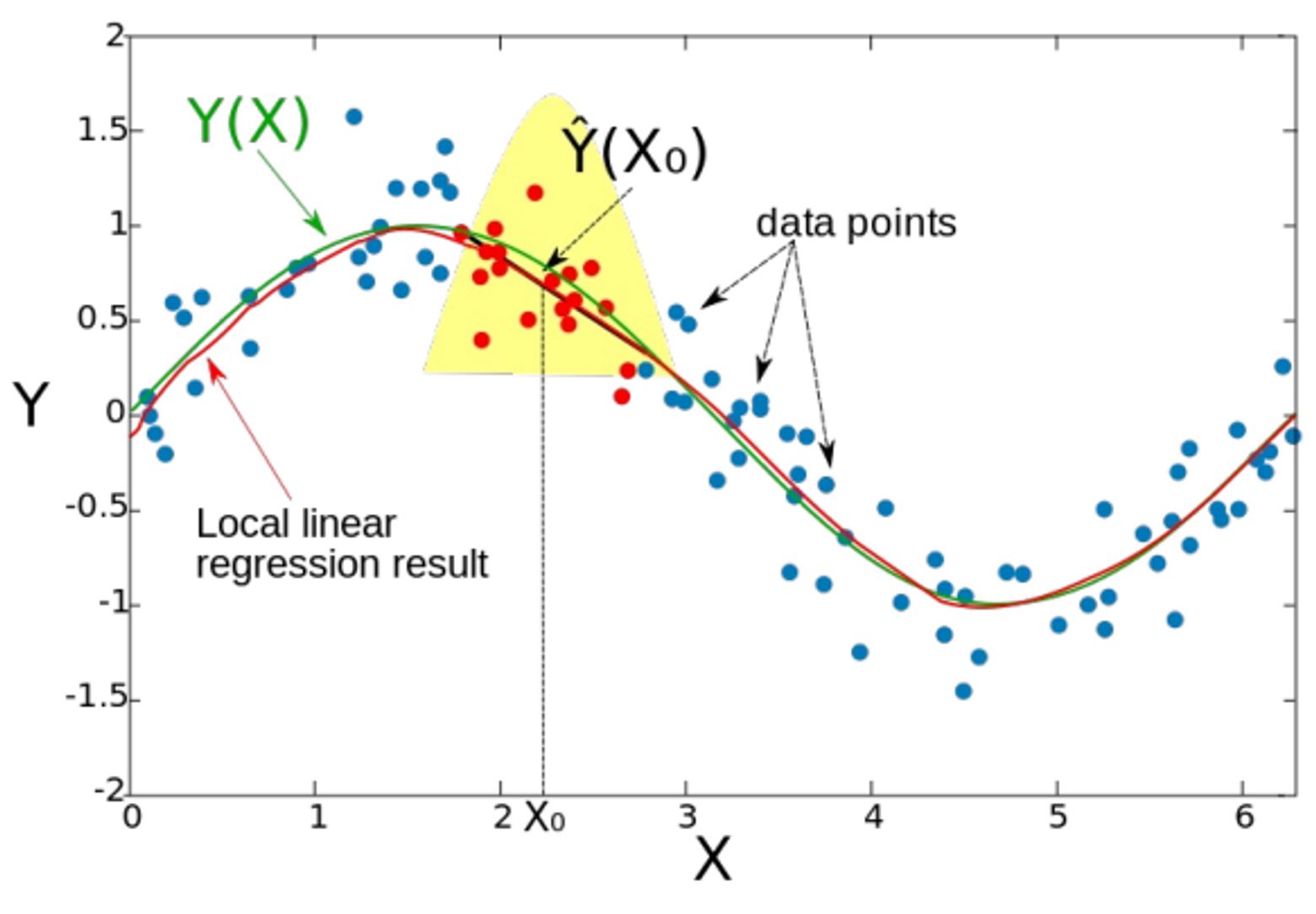
局部加权

在线性回归中引入近邻思想（没懂）：

$$\begin{gathered} \widehat{ϵ}(h)=\sum _{i=1}^n{q}_i(h({\mathit{x}}_i)-y_i{)}^2 \\ {q}_i=\exp (-\frac{({\mathit{x}}_i-\mathit{x}{)}^2}{2{\sigma }^2}) \end{gathered}$$

多选题：以下说法正确的是：

• 当类别数较大时，KNN 算法比线性模型更适合
• 使用 GD 或 SGD 求解线性模型，可在线性时间内求出全局最优解
• SGD 比 GD 单步更快，但需要更多迭代次数，因此收敛时间更长
• 使用基函数的线性模型也可以处理非线性问题，但需要特征工程

解答：线性模型是凸函数，可以求到全局最优解。SGD 和 GD 的收敛速率一样，但是单步更快，迭代次数更多，SGD 在实践中远远快于 GD，尤其是大规模样本，小到 LM 和 SVM，大到神经网络，全部用 SGD 进行迭代。线性时间就是和样本数/特征维数成正比（遍历数据所需要的时间）。

正则化

过拟合

高阶多项式的好处是：拟合数据的能力更强，但是过于高次的多项式容易拟合噪声 fit noise，产生过拟合 overfitting。同时另一种过拟合现象是如何实现分布外泛化，即训练数据只收集了一部分，在未收集到数据的区域，机器学习模型往往会失效——迁移学习。