第二章 K 近邻

机器学习对数据有很多不同的视角进行处理：代数视角，统计视角，几何视角等。K 近邻，KNN 就是一个几何视角。我们通常会对数据进行特征提取，得到一个高维的特征向量，而这些特征向量就存在于高维欧氏空间中。以 $d$ 维为例，在 $d$ 维欧氏空间中，我们可以定义距离的概念，从而计算不同特征向量之间的相似度。

在这个模型中，我们有一个基本假设：相似的数据应该具有相似的标签/类别/语义，也就是所谓的物以类聚 Birds of a feather flock together。但是近邻法是一种分类方法，而不是聚类方法。

近邻方法

最近邻

近邻 Nearest-Neighbor，NN：表示和某个数据点距离最近的数据点。以二维空间为例，我们定义样本点 ${\mathit{x}}_i$ 和 ${\mathit{x}}_j$ 之间的欧氏距离为：

$$D({\mathit{x}}_i,{\mathit{x}}_j)=\sqrt{\sum _{k=1}^d(x_{ik}-x_{jk}{)}^2}=\sqrt{(x_{i1}-x_{j1}{)}^2+(x_{i2}-x_{j2}{)}^2}$$

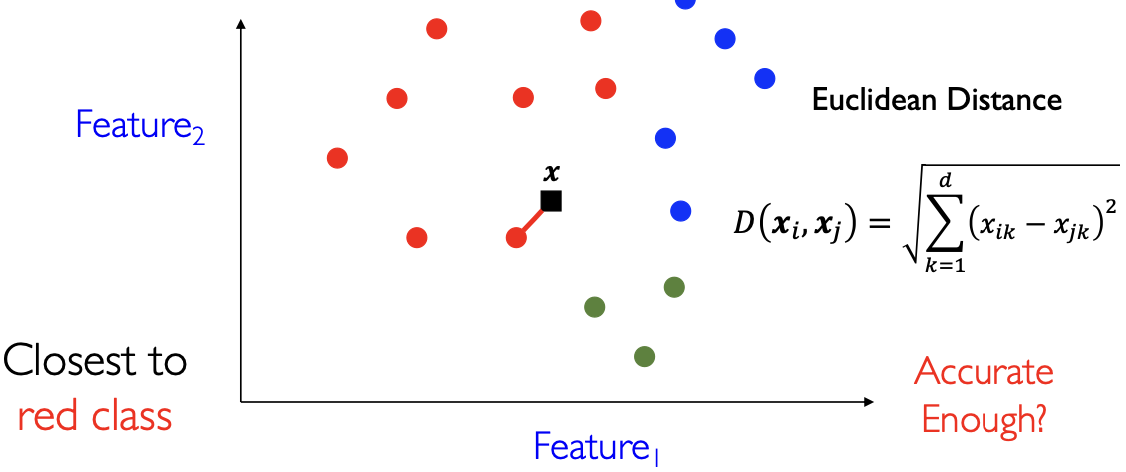
首先对于训练数据，我们将其画在二维平面中。对于验证集中任何一个的样本点 $\mathit{x}$，我们计算找到它的最近邻（这里需要计算它和所有点的距离，再排序）。我们发现它的最近邻是一个红色点，因此，将该样本点分类为红色。

K 近邻

K 近邻，KNN 就是考虑样本点的 $k$ 个邻居。假设 $k=5$，那么对于验证集中任何一个的样本点 $\mathit{x}$，我们计算找到离它最近的 $5$ 个样本点，根据邻居样本点的标签投票结果作为该样本点的预测分类结果。

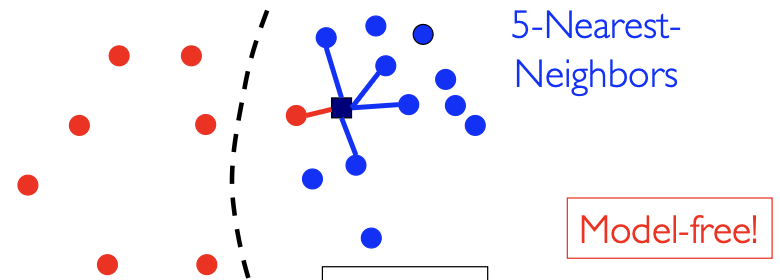
如图所示，尽管样本点 $\mathit{x}$ 的最近邻是红色点，但是显然将其分类为蓝色点更合理。一般的，我们取 $k$ 为奇数而非偶数，这是为了避免平票。

K 近邻方法非常简单，但是它是否能奏效 work 呢？1969 年由 Cover & Hart 证明了 K 近邻方法是对连续分布的一个很好的逼近器。他们证明了，如果数据可以较好地划分，那么 K 近邻方法可以收敛到一个几乎完美的解，错误率很低：

$$\underset{n\to \mathrm{\infty }}{lim}{ϵ}_{\mathrm{KNN}}(n)\le 2{ϵ}^{\ast }(1-{ϵ}^{\ast })$$

其中 ${ϵ}^{\ast }$ 是贝叶斯错误率 Bayes Error，$0<{ϵ}^{\ast }\le 1$，表示数据的固有错误率/最小错误率：即用一个真值函数对数据集进行分类时所造成的错误率。它可以完美解决贝叶斯错误率不太高（例如 1% 左右），但是分布复杂的问题。

例如这种 S 形分布的异或问题，大多数参数分布方法都不能很好地解决。当然，近邻方法需要足够多的训练数据作为支撑。

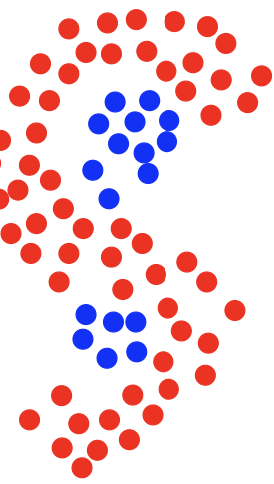
同时 K 近邻是经验有效 Empirical Efficacy 的，即在很多领域都已经有了很好的应用。

超参数

K 近邻中只有唯一一个超参数 $k$：$k$ 越大，分类面越光滑；$k$ 越小，分类面越崎岖。因此最近邻方法是一个很容易过拟合的方法，太大的 $k$ 又会导致决策面太简单，导致欠拟合。实际调参过程中我们就需要选择合适的 $k$，使得验证集上的错误率最小：

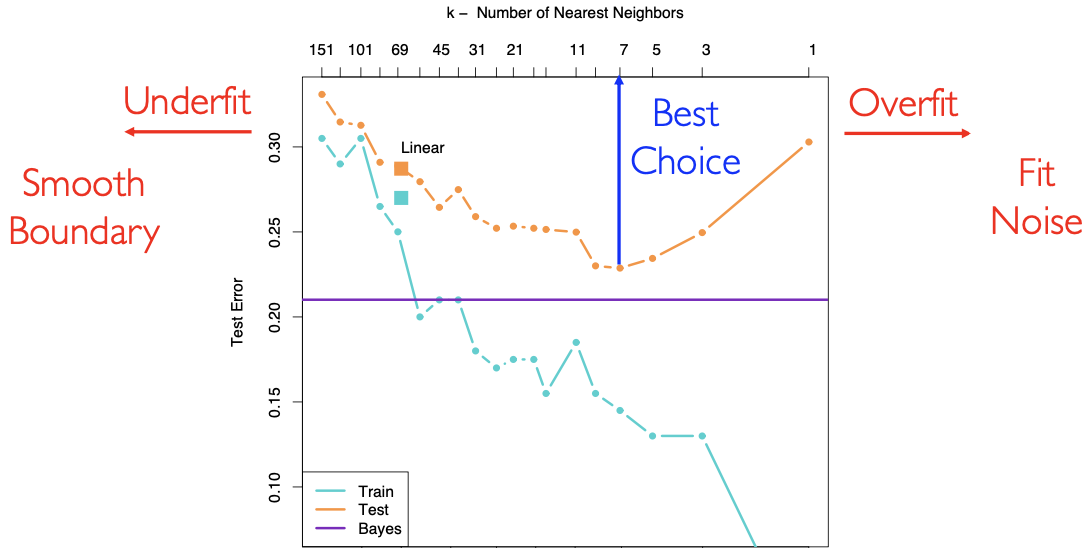
这是一张调参图。可以看到：$k$ 越大，训练集错误率越高，$k$ 越小，训练集错误率越低。但是只有当 $k=7$ 时，测试集错误率才达到最低（不能用这个来调参！图中不是很严谨）。应该还画一条验证集错误率曲线，取其中最低时的超参数，如果此时不为 7，也要取，否则就是作弊。

归纳偏好

K 近邻有两个归纳偏好 Inductive bias：即人为设置的前提条件：

• 欧氏空间中距离相近的点具有相似的标签
• 欧氏空间中不同维度之间是平等的：这是因为我们在计算欧氏距离时各维度权重为 1

这就导致如果不同维度特征的量纲差距较大时，直接使用 K 近邻法得到的决策面不好，如下图横轴为身高，米为单位；纵轴为体重，斤为单位：

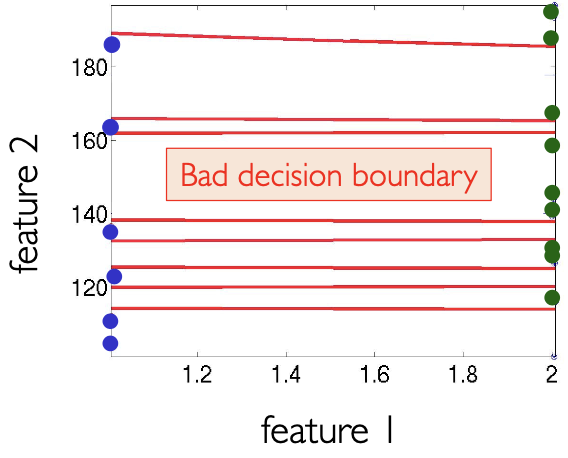
特征归一化

因此，我们需要做特征归一化 Feature Normalization，将每个特征都归一化为均值为 $0$，方差为 $1$。例如给定一个 $d$ 维训练样本，我们对其中的每个维度 $j$，都先求出该维度下所有数据的均值和方差：

$$\begin{array}{rlr}& {\mu }_j=\frac{1}{N}\sum _{i=1}^N{x}_{ij}& {\sigma }_j=\sqrt{\frac{1}{N}\sum _{i=1}^N(x_{ij}-{\mu }_j{)}^2}\end{array}$$

随后将该维度归一化为：

$${\hat{x}}_{ij}\leftarrow \frac{x_{ij}-{\mu }_j}{{\sigma }_j}$$

此时每一个维度从统计意义上来说都是均值为 $0$，方差为 $1$ 的分布。此时 K 近邻法就能学出正确的决策面。因此我们知道了这个先验知识：K 近邻法是对特征的取值范围敏感的，而之后所学的线性模型，神经网络，SVM 是否对特征的取值范围敏感呢？这是我们之后要学习的知识。

距离选择

• 余弦距离 Cosine Distance：$\cos ({\mathit{x}}_i,{\mathit{x}}_j)=\frac{⟨{\mathit{x}}_i,{\mathit{x}}_j⟩}{\parallel {\mathit{x}}_i\parallel \parallel {\mathit{x}}_j\parallel }$
  • 两个向量夹角的余弦值大小
• 闵可夫斯基距离 Minkowski Distance：$D_p({\mathit{x}}_i,{\mathit{x}}_j)=\sqrt[p]{\sum _{k=1}^d|x_{ik}-x_{jk}{|}^p}$
  • $p=1$ 时为曼哈顿距离/城市块距离
  • $p=2$ 时为欧氏距离
• 马式距离 Mahalanobis Distance：$D_M({\mathit{x}}_i,{\mathit{x}}_j)=\sqrt{({\mathit{x}}_i-{\mathit{x}}_j{)}^{\text{T}}\mathit{M}({\mathit{x}}_i-{\mathit{x}}_j)}$
  • $\mathit{M}$ 是正定矩阵，一般是单位阵或对角阵，由先验知识确定
  • $\mathit{M}=\mathit{I}$ 时为欧氏距离
  • $\mathit{M}$ 为对角阵时刻画了特征的重要性，从数据中学习 $\mathit{M}$ 被称为度量学习 Metric Learning
• 还有其他距离：https://en.wikipedia.org/wiki/Distance
  • 总结：没有一个距离总是表现的比其他距离好，就和算法一样

加权 K 近邻

普通 K 近邻 Vanilla KNN 使用少数服从多数的投票机制 majority vote 来预测离散值输出。而加权 K 近邻 Weighted KNN 则认为越近的邻居拥有更高的权重，加权方法也是机器学习中的一个重要方法。下面是以距离为权重的两个例子，其中 ${\mathrm{KNN}}_c(\mathit{x})$ 表示样本点的所有 $k$ 个近邻中类别为 $c$ 的训练数据点：

分类问题：越近的样本投票时权重更大：

$$\hat{y}={\text{argmax}}_{c\in \mathcal{Y}}\sum _{{\mathit{x}}^{\prime }\in {\mathrm{KNN}}_c(\mathit{x})}{\displaystyle \frac{1}{D(\mathit{x},{\mathit{x}}^{\prime }{)}^2}}$$

回归问题：KNN 也可以做回归问题，输出值为 $k$ 个近邻输出值的（加权）平均数：

$$\hat{y}=\sum _{{\mathit{x}}^{\prime }\in \mathrm{KNN}(\mathit{x})}{\displaystyle \frac{1}{D(\mathit{x},{\mathit{x}}^{\prime }{)}^2}}{y}^{\prime }$$

加权后可以使得分类面更加细致。除了上面给出的平方反比函数，还有很多加权函数。

近邻中心分类器

近邻中心分类器 Nearest Centroid Classifier 是对 KNN 算法的一点简单改进：假设给定训练数据集 $\{{\mathit{x}}_i,y_i{\}}_{i=1}^N$，其中标签为 $y_i\in \mathcal{Y}$，我们认为每个类别都有自己的中心，计算类别的中心 centroid：

$${\mathit{\mu }}_c=\frac{1}{|N_c|}\sum _{y_i=c}{\mathit{x}}_i\in {\mathbb{R}}^d$$

在预测时，只需要比较验证集样本点 $\mathit{x}$ 和 $C$ 个类别中心之间的距离，距离最近的作为标签输出：

$$\hat{y}={\text{argmin}}_{c\in \mathcal{Y}}\parallel \mathit{x}-{\mathit{\mu }}_c\parallel$$

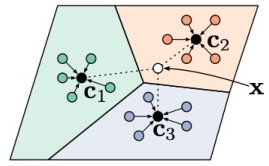
近邻中心分类器的好处是非常快，对比普通的 KNN 算法：

	近邻中心分类器	普通 KNN
训练	计算每个类别的中心 $\mathcal{O}(Nd)$	不需要训练
验证	比较样本和类别中心距离 $\mathcal{O}(Cd)$	计算样本和所有数据点之间的距离并取 $k$ 个近邻 $\mathcal{O}(Nd)$

一般来说都有 $N\gg C$，因此近邻中心分类器在验证/测试时远远快于普通 KNN。

近邻中心分类器有独特的归纳偏好/归纳假设/适用范围：它认为每个类中的数据点都服从以类中心为均值，某个协方差矩阵（单位阵）为方差的高斯分布。当我们做完归一化处理之后，数据点就都服从协方差矩阵为单位阵（但是均值不同）的高斯分布。反过来想，如果数据点都服从上述假设，那么显然距离类中心最近的点自然落入该类之中，因为高斯分布的等值线是形状相同的同心圆。

这个假设是一个非常强的假设：每个类中的数据点都服从以单位阵为方差，以类中心为均值的高斯分布，现实世界中基本不存在这种数据点。那么我们什么时候可以使用这个分类器呢？机器学习中有一个重要原理：越强的假设意味着越多的先验知识，也就意味着越少的数据量。因此近邻中心分类器可以用于小样本学习 Few-Shot Learning，FSL。目前仍然是小样本学习分类器中的最好 State-Of-The-Art，SOTA。

维度灾难

维度诅咒 Curse of Dimensionality 是导致很多机器学习算法失效的重要原因。

近邻搜索

近邻搜索：从所有的数据点中找到和某个点距离最近的 $k$ 个数据点。因此，排序算法也可以理解为最严格的近邻搜索算法。假设现有 $n$ 个训练样本，每个样本具有 $d$ 个维度。对于普通 KNN 算法而言，训练只需要 $\mathcal{O}(1)$ 的时间，但是验证需要 $\mathcal{O}(nd)$ 时间去找到最近的 $k$ 个样本。而我们知道，普通 KNN 算法的先验知识是很弱的，因此需要足够多的数据才有较好的分类结果，也就是 $n$ 需要取得很大。

如果对于 KNN 算法采用一种新式数据结构 k-d 树来存储，那么需要 $\mathcal{O}(dn\log n)$ 时间训练/构建一棵 k-d 树，验证时需要 $\mathcal{O}(2^d\log n)$ 时间用于 k-d 树做近邻搜索查询，有效降低了时间复杂度，但同时我们注意到时间复杂度和维度 $d$ 有关，因此只有在 $n\gg 2^d$ 的时候才使用 k-d 树，同时如果训练数据本身的维度过大，验证时间复杂度也会很大。

综上可知，使用 KNN 算法，只有在训练样本足够多，样本数据维度比较小的时候才有效。也就是说 KNN 算法在低维大规模数据方面很有效。

对于高维大规模数据，目前比较好用的方法是快速近似近邻搜索 Fast Approximate Nearest Neighbor Search，我们常用的以图搜图就是这个技术。

维度诅咒

上面是以近邻搜索的角度介绍了维度越高，搜索速度越慢这一维度诅咒现象。接下来我们介绍一种更加严重的维度诅咒现象：首先，我们的高维数据一般会分布在某个低维流形 manifold 之上，而不是弥散在整个高维空间中（好比宇宙和恒星），但低维流形的具体形状是一个先验知识，我们并不知道。而如果高维数据充分随机分布在高维空间中，此时我们会发现：

假设我们每一维的数据都位于 $[0,1]$ 之间，那么对于体积为 1 的超正方体，体积是它的 1/10 的小立方体的边长将会是 $\sqrt[10]{0.1}\approx 0.8$，0.8 和 1 非常近，此时很难说它们构成一个“近邻”，计算可知欧氏距离大约为 $\sqrt{6.4}\approx 2.53$。从这个例子可以看出，维度越高数据之间的距离越大，整个高维空间越空旷，高维空间中的点哪怕坐标差距不大，也是很遥远的——事实上都是孤立点。

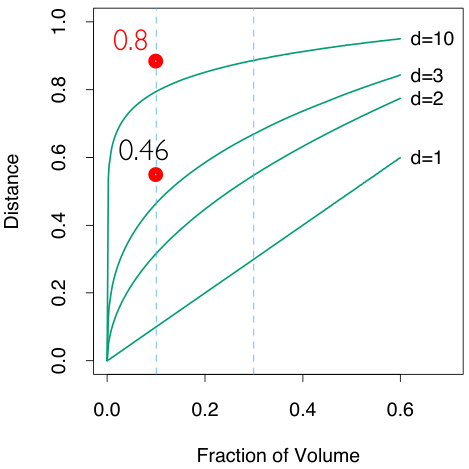
因此，为了获得足够多的信息，我们需要数据条数 $n$ 与数据维度 $d$ 呈指数 exponential 关系。

《ESL》：考虑 $n$ 个独立同分布的 $d$ 维随机变量 $X_1,X_2,\cdots ,X_n$ 在单位超球上成均匀分布 uniform distribution。计算与原点最近的点中的和原点距离的中位数是：

$$\mathrm{med}(d,n)={(1-{\displaystyle \frac{1}{2^{\frac{1}{n}}}})}^{\frac{1}{d}}$$

当 n=500，d=10 时可知 med=0.52，此时也就是说，大多数数据点不再靠近球心，而是靠近球壳。也就是说靠近球壳的体积占据了整个单位超球的绝大部分（几何概型）因此几乎所有统计分布/直觉 intuition 都失效了，例如高斯分布的绝大多数不再位于均值附近，而是位于边缘部分。因此 KNN 也不再适用！

虽然总是在说维度诅咒，但是流形分布这个先验知识让我们有了继续学习高维数据的能力！我们机器学习的目的就是学习到这个流形，深度学习某种意义上就解决了这个问题——在深度特征意义下高维数据一般就位于了某个流行之上。

总结

• 什么时候使用 KNN：
  • 特征维度比较低，单个数据点不要有太多特征 Few attributes per instance
  • 训练样本条数足够多，足以对抗维度诅咒（维度越高数据距离越远，不是近邻）
• 优点：
  • 无脑 agnostically 学习复杂的目标函数
  • 不会损失信息：存储训练原始数据
  • 训练数据条数可以很大：搜索引擎广泛运用 KNN 技术
  • 类别数也可以很大：大多数机器学习算法在类别数特别大的时候会失效
• 缺点：
  • 推理得非常慢 Slow at inference time，因此一定需要加速：快速近似近邻搜索：FAISS
  • 高维不是很有效：维度诅咒
  • 很容易被无关特征欺骗：特征工程 feature engineering 很重要