第三章 卷积神经网络
3.1 计算机视觉
卷积网络 Convolutional Network,也称为卷积神经网络。主要用于处理计算机视觉方面的问题,计算机视觉的基本问题是图像识别,人类很善于做图像的多角度描述:内容/情感,但是计算机不能,计算机只能描述内容,包括:物体检测、情感识别、对象关系推理:其中对象关系推理是最难的。

还是回到仿生学的观点:神经科学研究发现,给猫一个视觉激励信号,大脑皮层中会有一个响应。这个过程中最重要的发现是有关“感受野 receptive field”的概念——大脑中的单个神经元只会关注输入激励中的一个特定区域,从而修改自身的激活状态。CS231 中指出:对人类的大脑研究也发现:拓扑意义上来说,相邻的神经元会解决视野之中相邻的区域,具有局部性。
- 简单功能细胞:光照方向
- 复杂功能细胞:运动方向、端点
这就启示我们以一种层次化表示的方式来学习特征:例如先从端点检测开始,再到五官检测,最后到人脸识别。因此为了模拟人脑的视觉系统,我们需要从数据中直接学习层次化的特征表示,并且不需要手工构造特征。
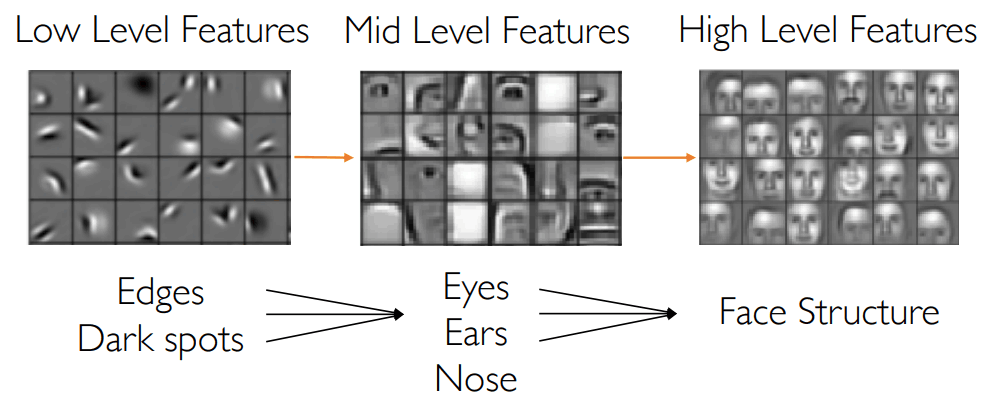
前面已经说了,MLP 是可以处理图像问题的,例如一张
3.1.1 卷积神经网络
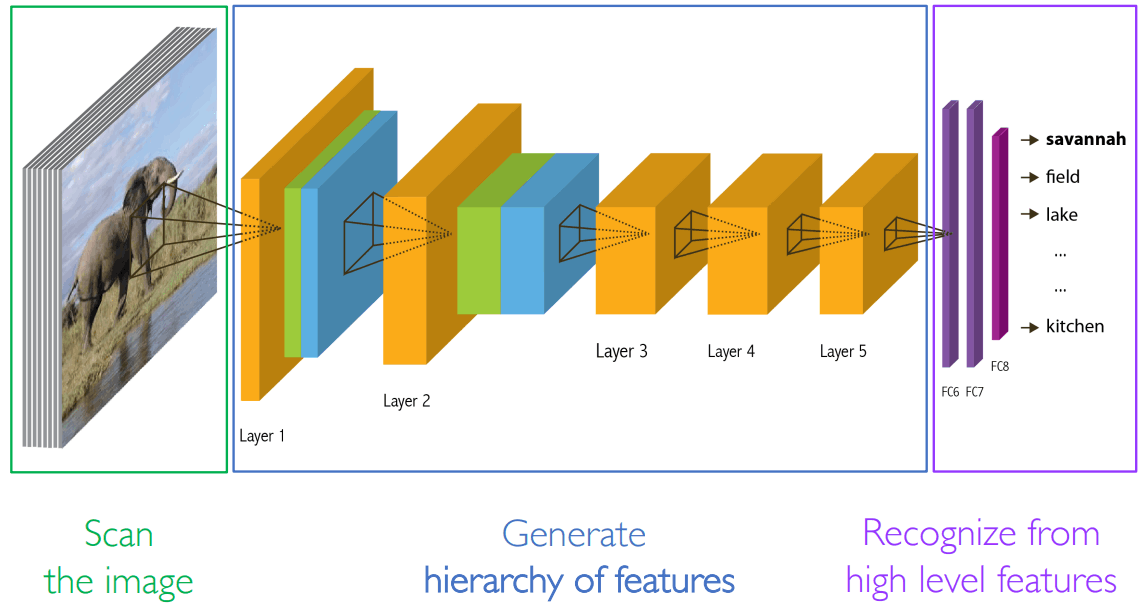
- 扫描图像,得到多维向量——张量 tensor
- 生成层次化特征,每一个 Layer 代表不同层次的特征
- 不同的视觉任务需要不同的特征,例如图像识别需要高层特征,图像生成需要底层特征
3.1.2 局部连接
受到“感受野”概念的启发,我们认为:每一层的神经元和上一层的局部区域连接:
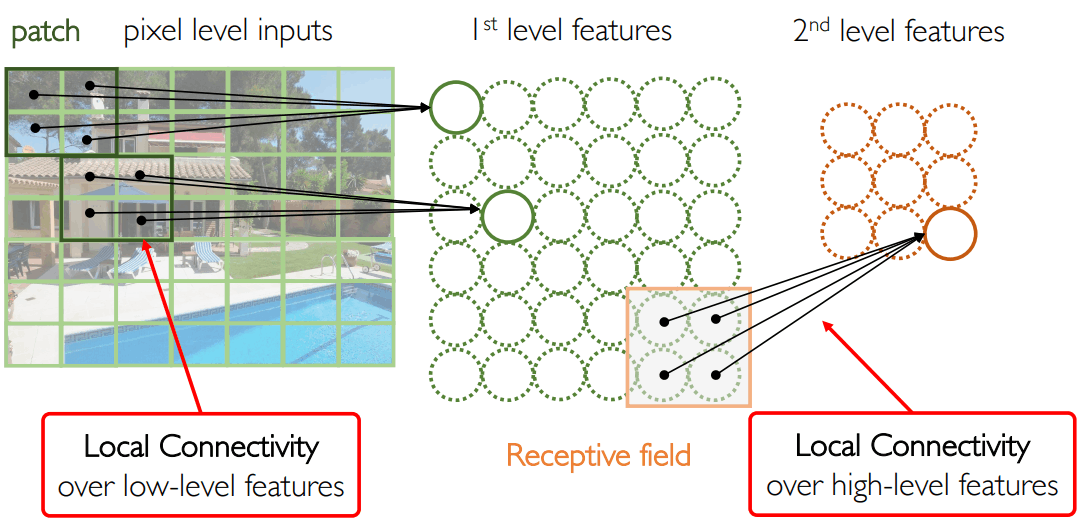
例如:第一层的左上角神经元和输入层的左上角四个像素点组成的 Patch 连接,说明它只能看到这四个像素点区域。其他层也是一样的。连接方式为对应连接,保持空间的相对位置关系。局部连接假设:识别只需要局部信息就够了,例如真正的人脸识别不一定需要看到整张脸,看到五官可能就够了。每个神经元只关注到输入空间中局部的区域。
3.1.3 参数共享
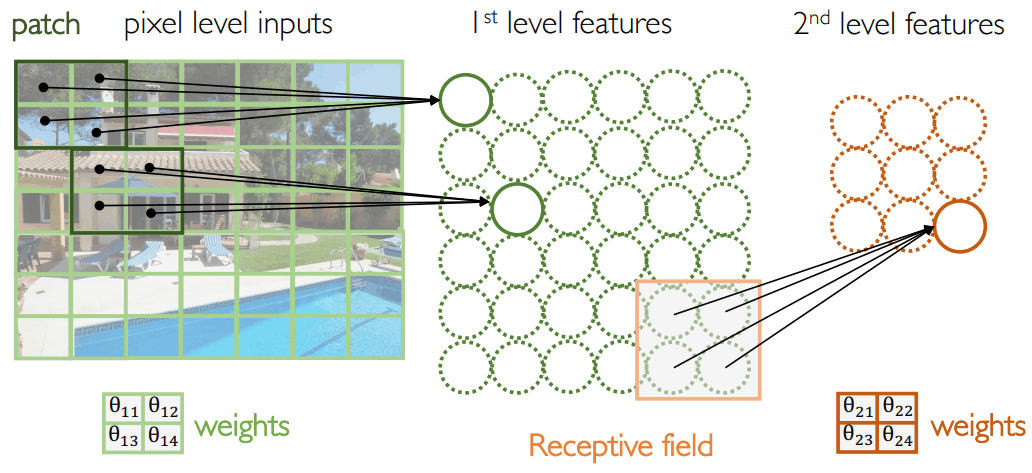
不同神经元对应的
3.1.4 卷积
给定两个连续函数
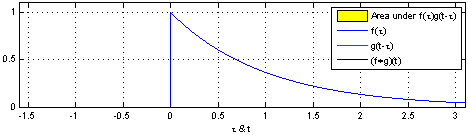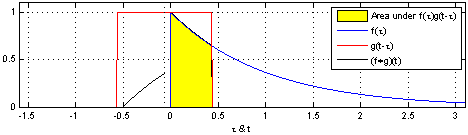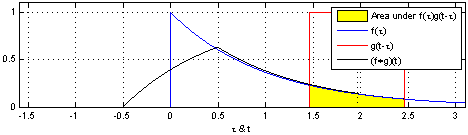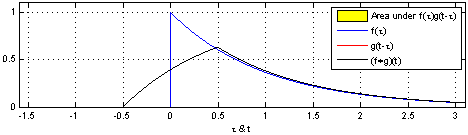
连续情况下:
离散情况下:
权重函数
3.1.5 互相关
有两个以时间
连续情况下:
离散情况下:
互相关可以发现两个信号之间重要的重叠部分。
3.1.6 卷积与互相关
卷积和互相关之间存在某个等式:
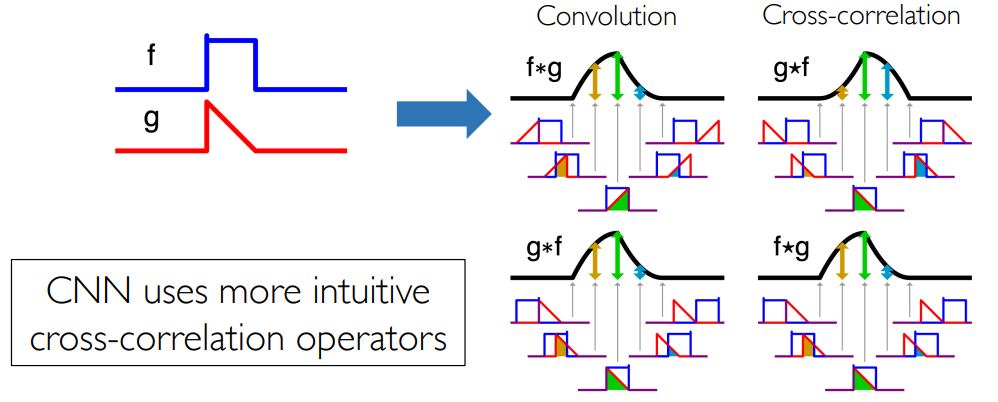
- 卷积操作:先反转
函数,再从左往右挪动 - 互相关操作:直接挪动,不需要反转
因此在卷积神经网络中,实际使用的是互相关算子:少一次反转操作,但其实和卷积是等价的。
3.2 基本概念
下面介绍卷积神经网络中的一些基本概念 notations:
卷积神经网络的输入是一张图像,通常有 RGB 三个通道,再加上宽和高,因此是一个张量:我们通常称之为 Volume/Tensor,同时也将通道 Channel 称为深度 Depth。
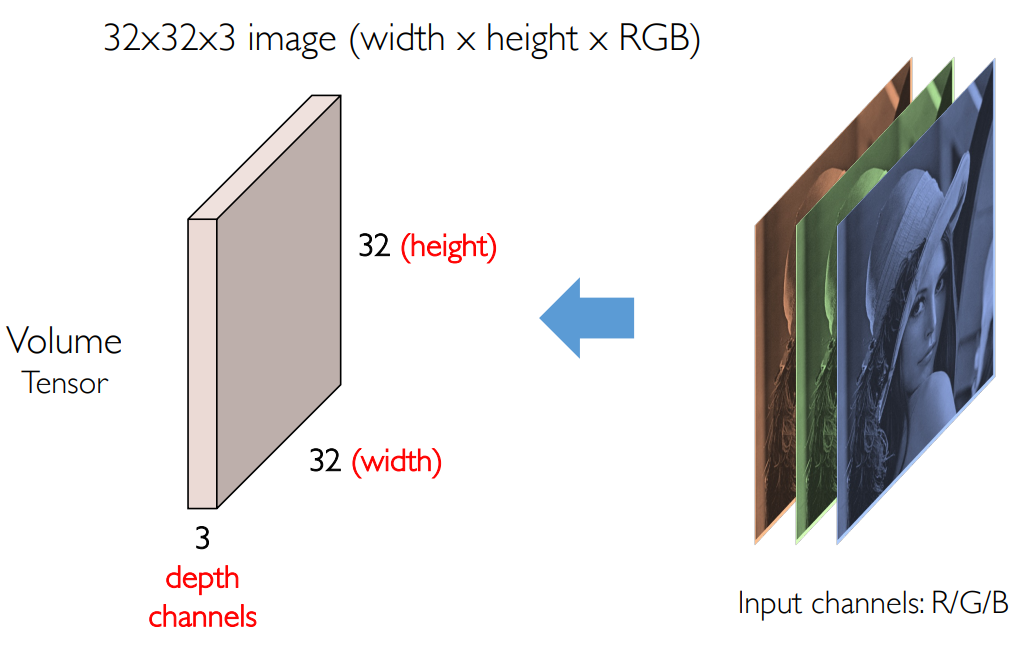
局部连接
然后找到一个权重函数矩阵,通常称之为卷积核 kernel/filter:例如可以取一个
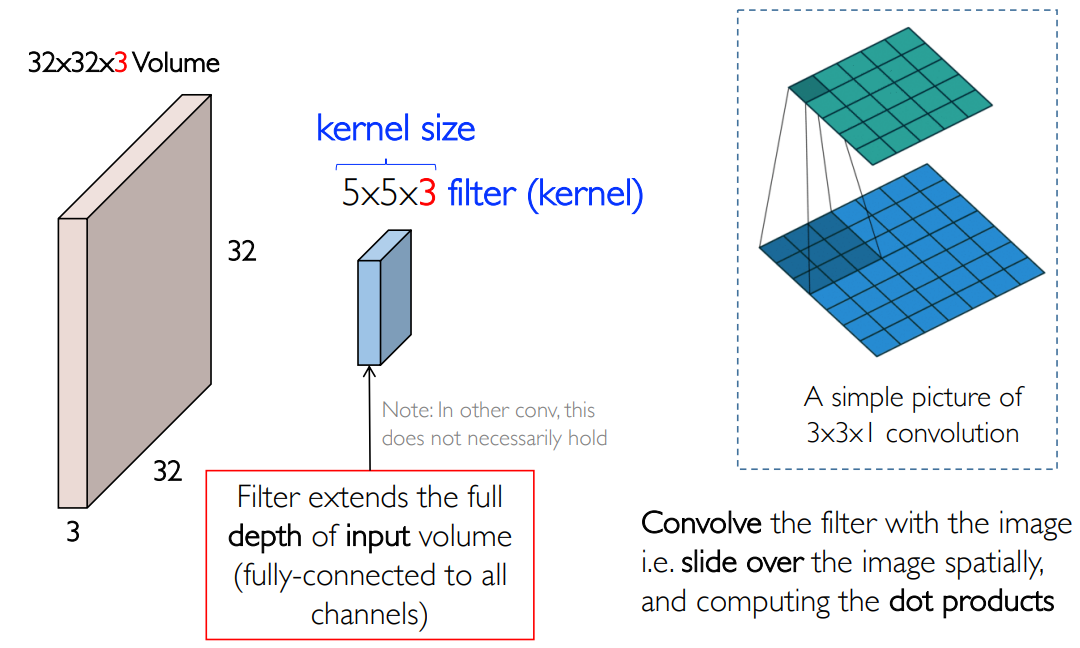
上面是卷积中的平移操作,下图给出了卷积中的求积分/求和操作:
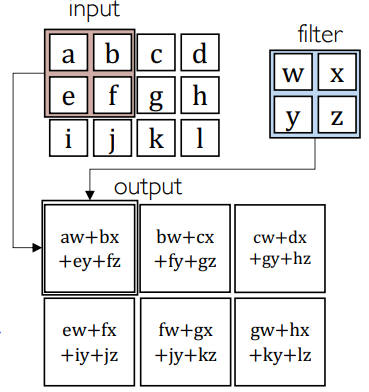
写出公式就是:
解读:输出空间 S 中
总结:
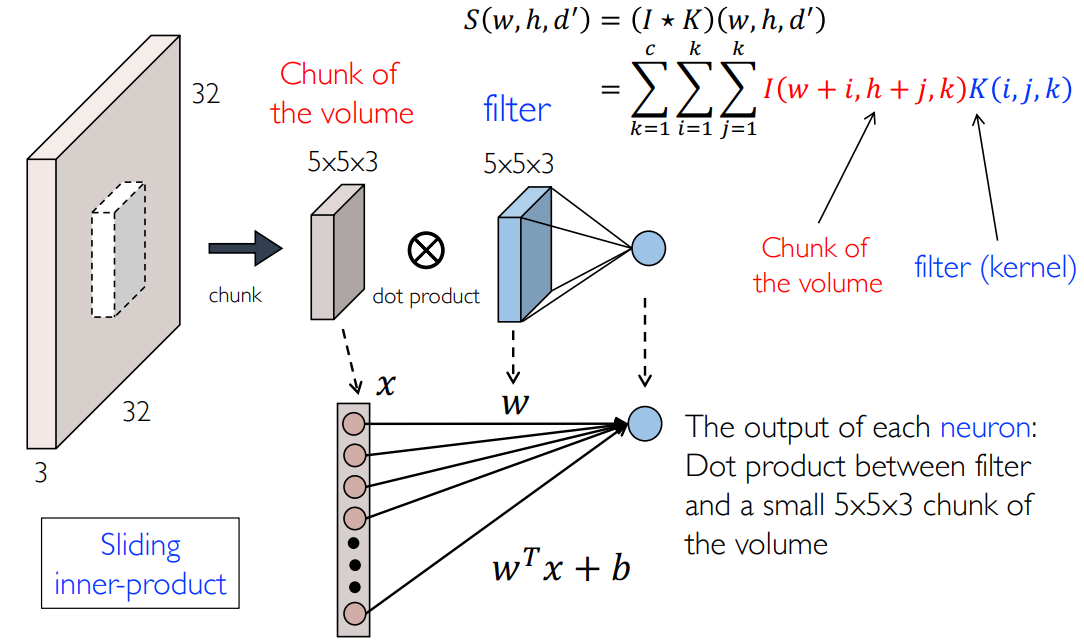
- 首先选取合适大小的卷积核 filter
- 然后在图像上滑动,取出与卷积核同样大小的块,称为 chunk
- 二者展开后做内积:
参数共享
实际上,我们并没有真正做到“滑动”,而是放了很多神经元,不用相同的参数矩阵进行计算,具体有多少个神经元呢?例如我们是
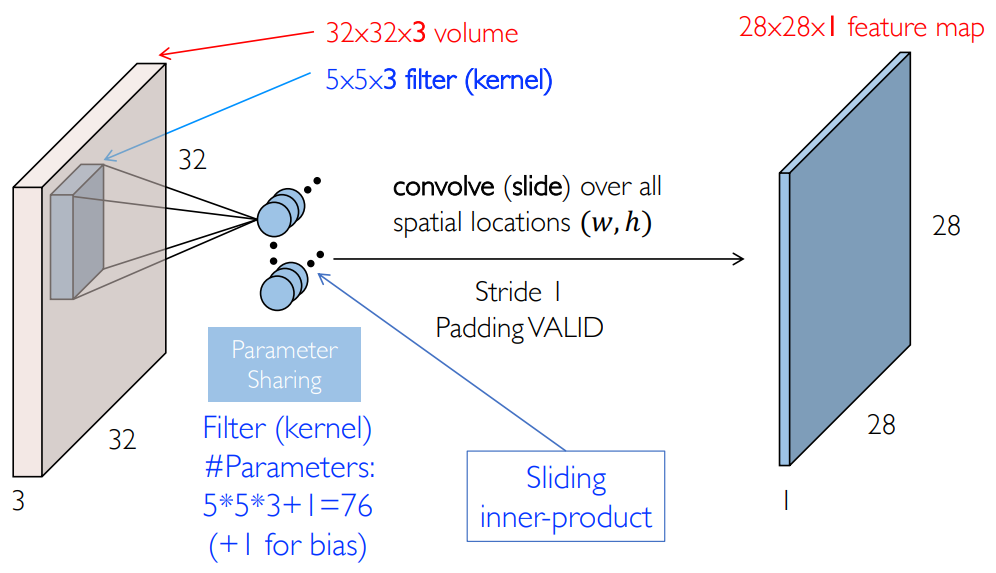
因此是一些简单的矩阵并行运算:所以用 GPU 来算比较快。
特征图
刚才说了,一个卷积核可以生成一张特征图,例如“眼睛”特征,那么如果我们需要“鼻子”特征,则需要定义一个新的卷积核。一般来说需要几十到几百个卷积核:
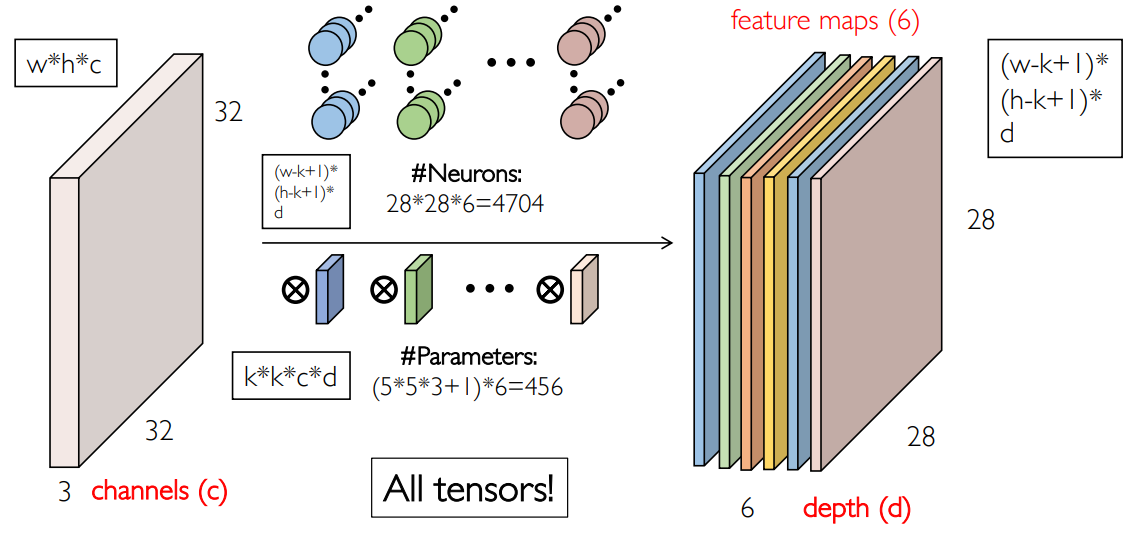
这就是一个典型的卷积层:输入是一个张量,输出是多张特征图构成的张量:
所有卷积核的参数量为:
卷积神经网络是一个参数量很小的网络,因此容量很小,避免过拟合,在数据量不是很大的时候是优先选择的方案。但是显存占用是很大的,因为特征图很大,需要存储每一层的激活值,用于计算反向传播。多个特征图组成了多通道的表征 representation,我们可以可视化每一个特征图。
空洞卷积
标准卷积是一个密集的卷积核,空洞卷积 dilated convolution 是在卷积核的参数之间插入一些漏空,如下图所示,红色点对应有参数的位置,两个红色之间间隔为 0 是 1-dilated conv,间隔为
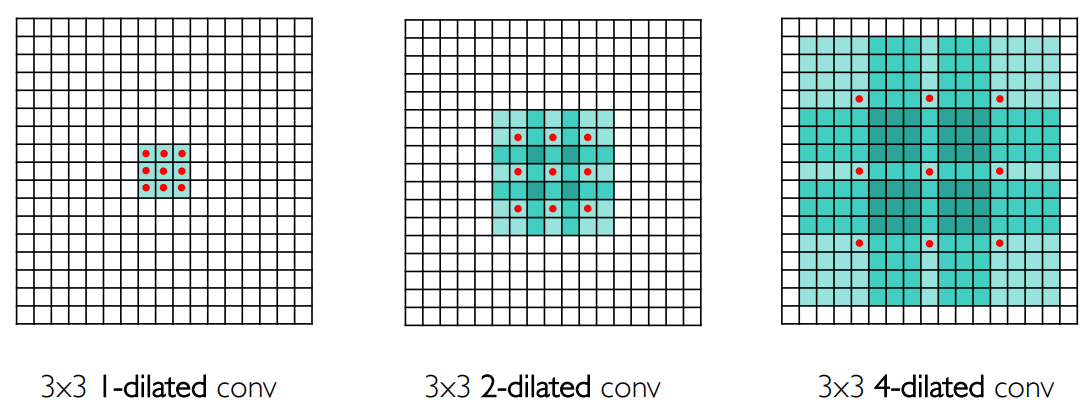
空洞卷积可以增加感受野。作者号称这个方法可以以指数的速度增加感受野,实际上有效感受野没有那么快的增加:Fisher Yu, Vladlen Koltun. Multi-Scale Context Aggregation by Dilated Convolutions. ICLR, 2016.
下图给出了常用的卷积方法:
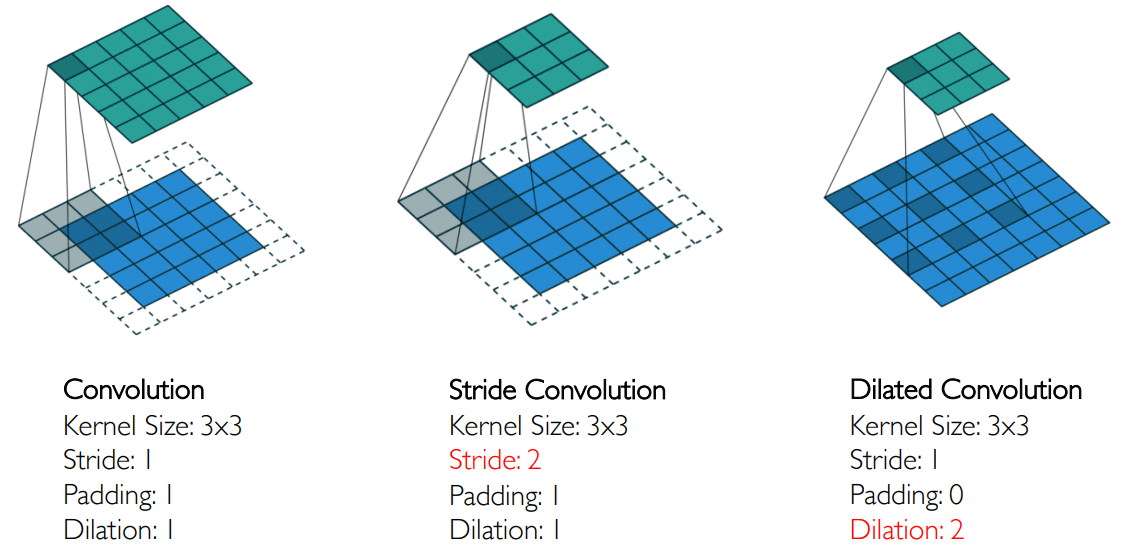
卷积算子
常见的卷积核算子:
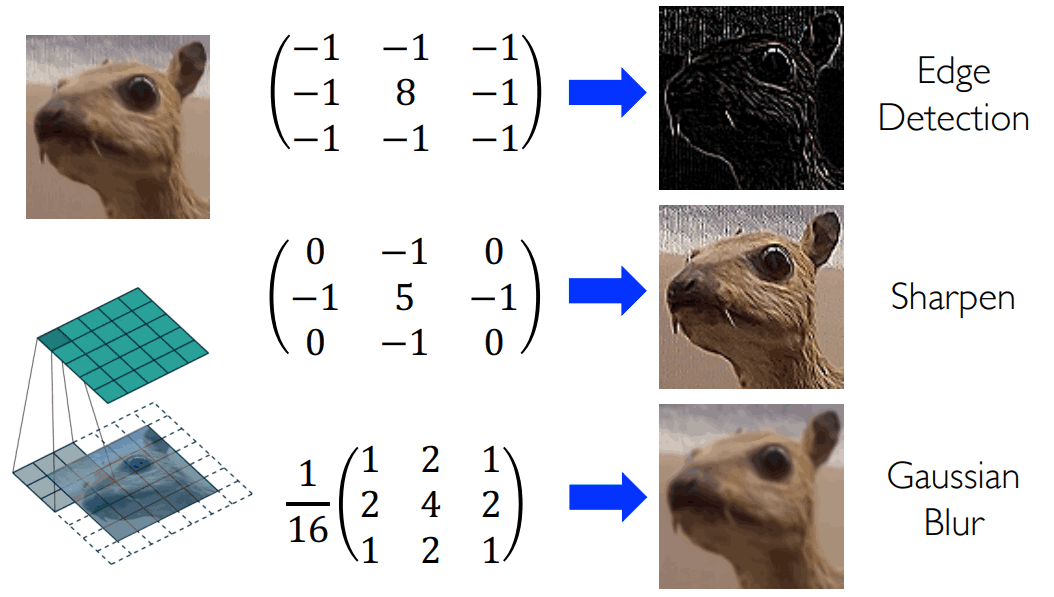
- 边缘检测算子:中间大,四周小:突出边缘中心的信息
- 锐化算子:相较于边缘算子保留了颜色信息
- 高斯模糊算子:权重按照二维高斯分布:可以模糊图像
单选题:以下关于卷积层的描述中,正确的是:
层通道数一定比 层多:错误,看卷积核的个数 - 卷积层的参数量与输入图像的长和宽无关:正确:
- 参数共享是指不同卷积层之间贡献卷积核参数:错误,同一卷积层内部共享
- 后层特征图的宽度由卷积核的通道数决定:错误,由卷积核的数目决定
步幅
步幅 stride 表示卷积核的移动速度,我们常用的都是步幅为 1 的卷积核,但是这样会导致一个很大的图在很小的卷积核下,生成的特征图过大。如果我们配置步幅为 2,那么可以进一步降低特征图的大小(这也是 CNN 调整特征图大小的主要办法):

填充
步幅过大,可能会导致不匹配!例如
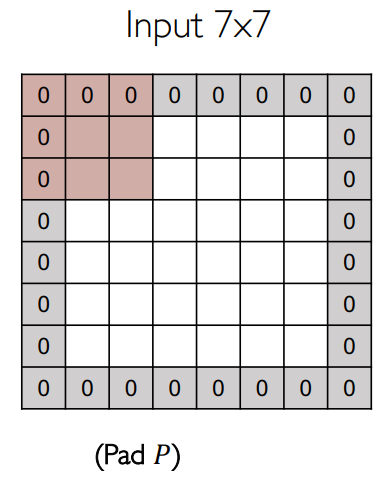
称为 padding=1。除了匹配,填充还可以提高特征图的大小,最后特征图的宽与高为:
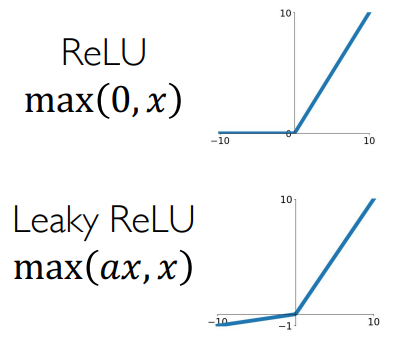
激活函数
引入过一个新的函数 Leaky ReLU,可能有些提升,但是一般还是用 ReLU:
卷积层参数配置
我们在写 PyTorch 的时候,卷积核的大小、个数都是需要自己配置的:
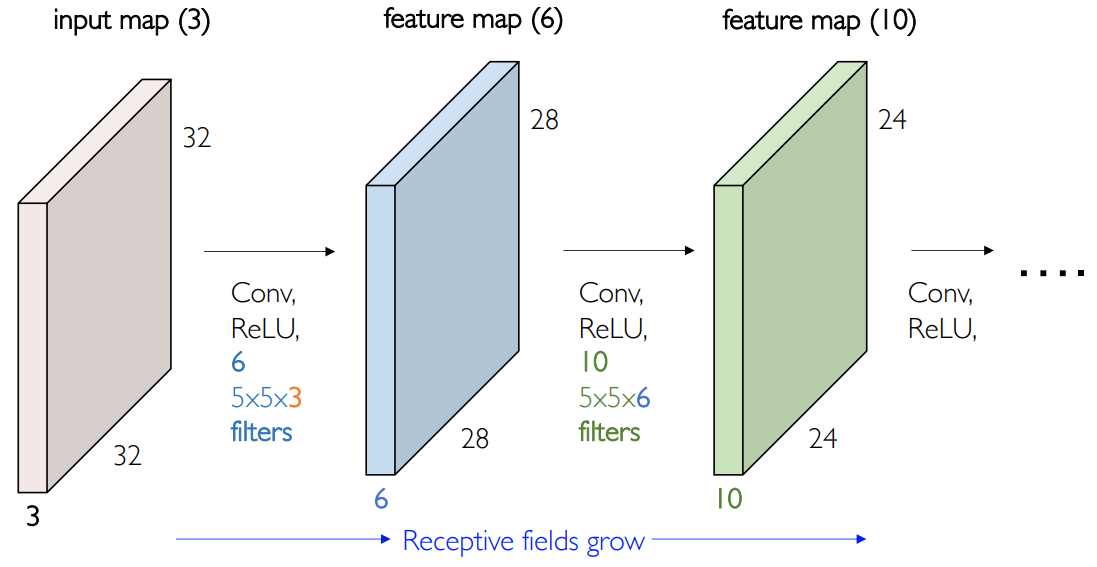
一般来说,特征图的大小要按照两倍衰减(需要有衰减,但是不能衰减太快!)
超参数
- 输入是一个张量:
- 卷积核的超参数:
- 卷积核的个数(下一层卷积核的深度):
- 感受野的大小(卷积核的大小):
- 步幅的长度:
- 填充的大小:
- 卷积核的个数(下一层卷积核的深度):
- 输出是一个张量:
- 这一层的参数量:
池化
池化 pooling 操作就是一个求平均的操作:最大值池化/平均值池化:
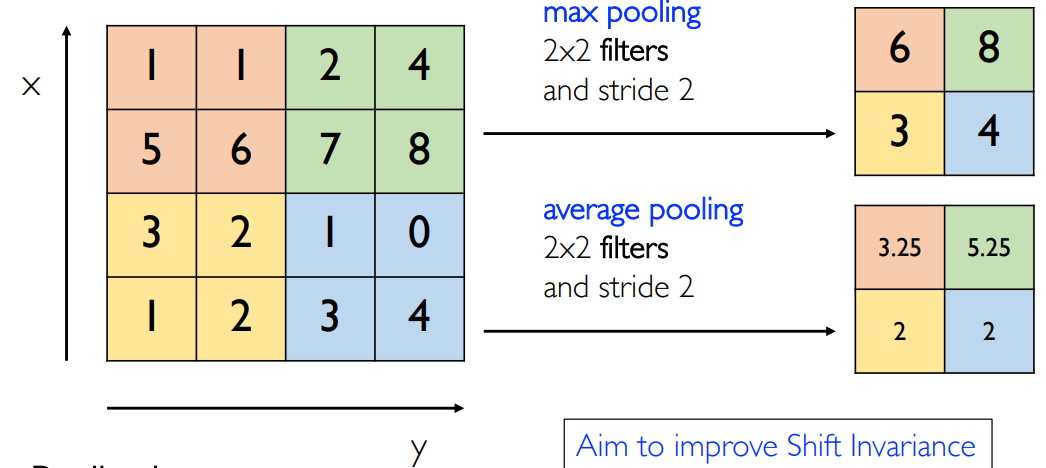
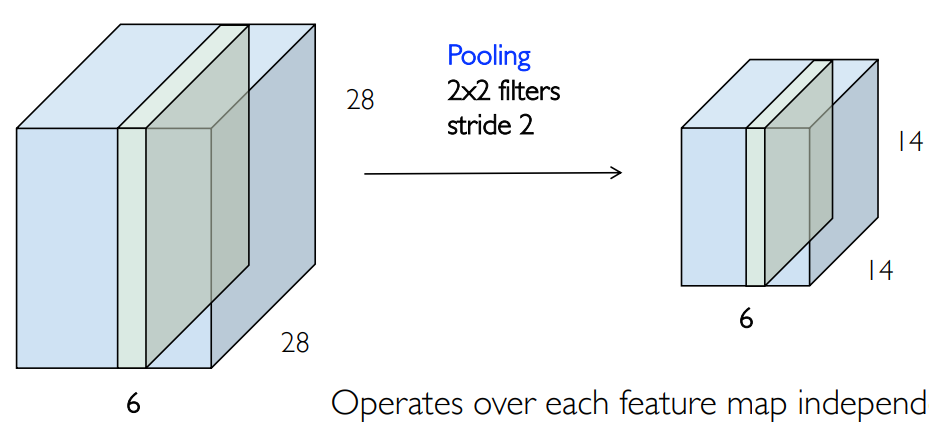
池化一开始是为了获取平移不变性的,但是后来发现没有这种性质,但是可以用来降低特征图的尺寸。因此在 CNN 网络中加入了池化层。池化不改变深度,但改变宽和高:
空间金字塔池化
这也是何恺明的工作,主要用于解决视觉中的空间多尺度问题。例如人脸和整个身体是不同尺度的对象,那么如何识别这种多尺度的对象以及它们的特征?如下图所示:特征图做不同粒度的池化操作,得到不同尺度的特征,然后将其输出到全连接层中:
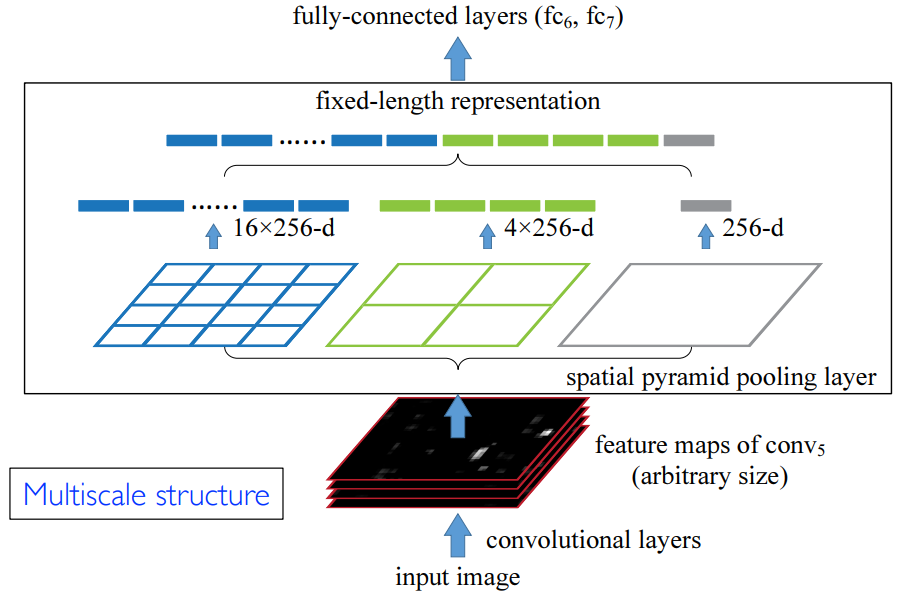
详见 K He et al. Spatial pyramid pooling in deep convolutional networks for visual recognition. ECCV 2014: 346-361.
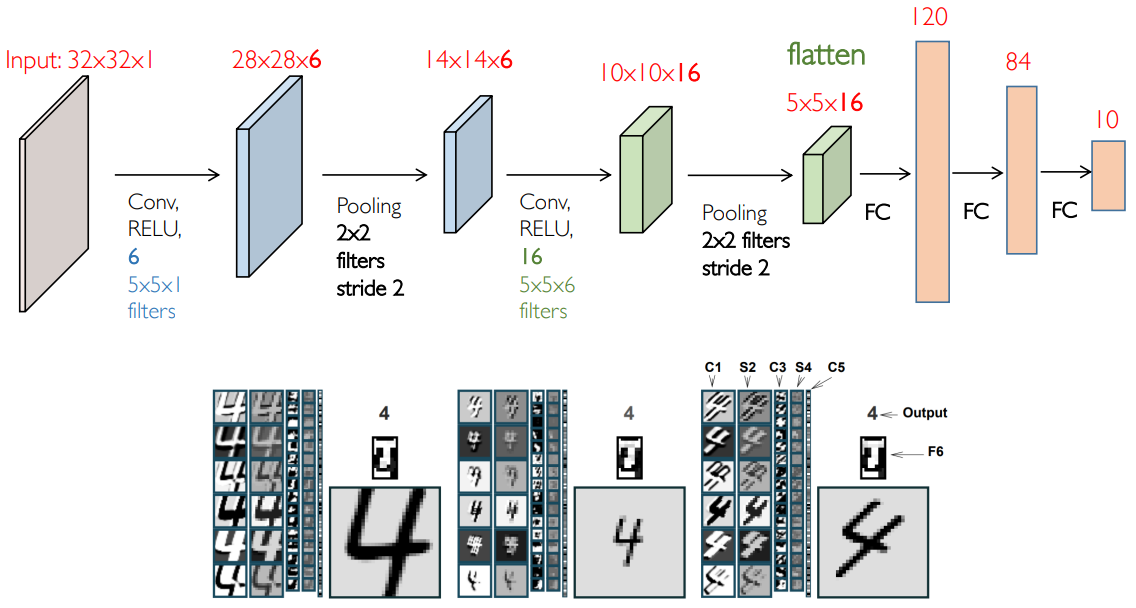
LeNet
介绍完上面这些基本工作之后,我们可以来搭积木了,这个领域的一个网络由 Yann LeCun 实现,Y. LeCun, L. Bottou, Y. Bengio, Gradient-based learning applied to document recognition, Proc. IEEE, 1998. (Cited 48907),这也是第一个可以工作的 CNN 模型,将其称为 LeNet:
AlexNet
Krizhevsky, Alex, Ilya Sutskever, Geoffrey E Hinton. ImageNet Classification with Deep Convolutional Neural Networks. NIPS, 2012. (Cited 116256) 是引用量仅次于 ResNet 的论文。
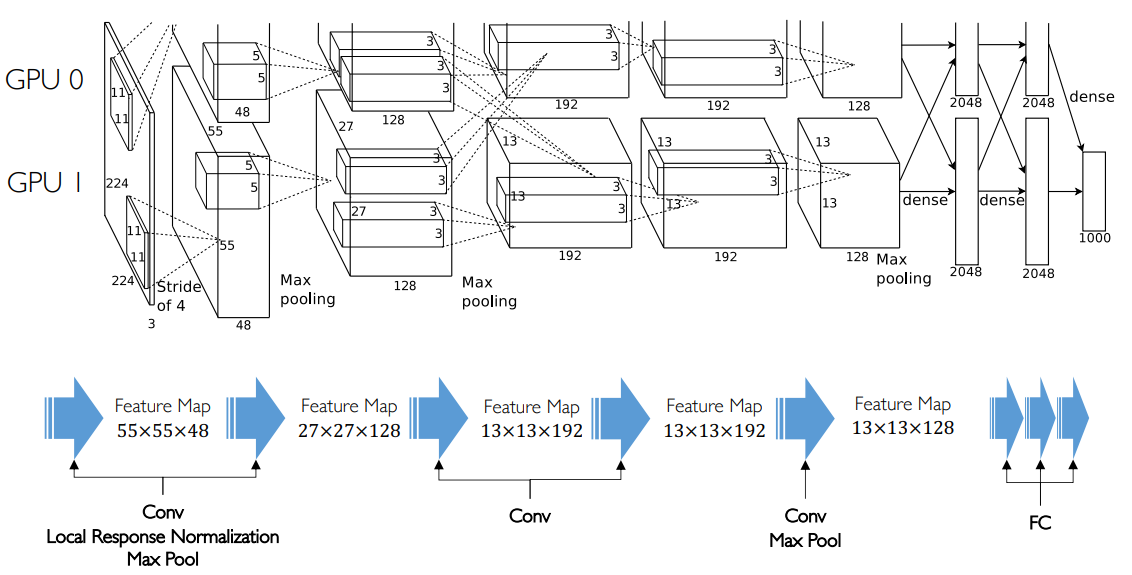
主要贡献:提出了通道拆分和通信,方便 GPU 并行训练。主要是工程上的贡献。
特征可视化
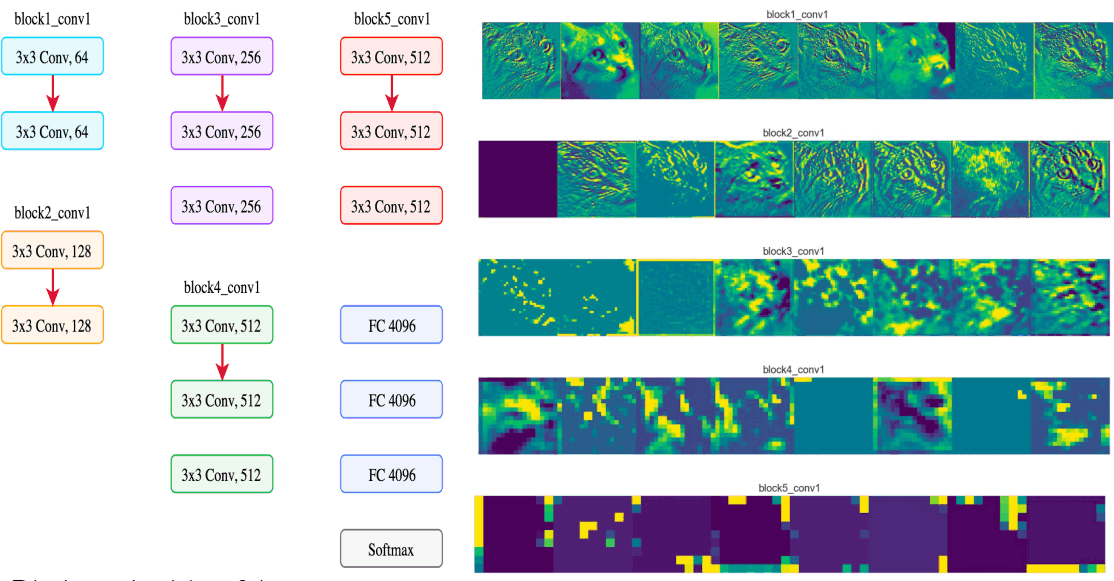
我们可以看出,一开始的图像很复杂,最后一层的图像就是散点图了,很简单,可能用一个线性超平面就能够将它们区分开来。神经网络变换就是一个从复杂函数到简单函数的过程。人脑系统能看懂复杂函数却看不懂简单函数,是因为人脑的视觉系统没有中间特征的残留。
参考:https://github.com/utkuozbulak/pytorch-cnn-visualizations
单选题:以下关于卷积神经网络的描述中,错误的是?
- 往往包含卷积层和池化层,但池化层使用渐少:正确,一般只有两个池化层
- 池化层试图增强平移不变性,但未实现该目标:正确
- 步幅(Stride)越大,卷积核参数量越小:错误,步幅与卷积核参数无关,与特征图大小有关
- 与 LeNet 相比,AlexNet 架构类似以但参数量更大:正确
反向传播算法
前向传播
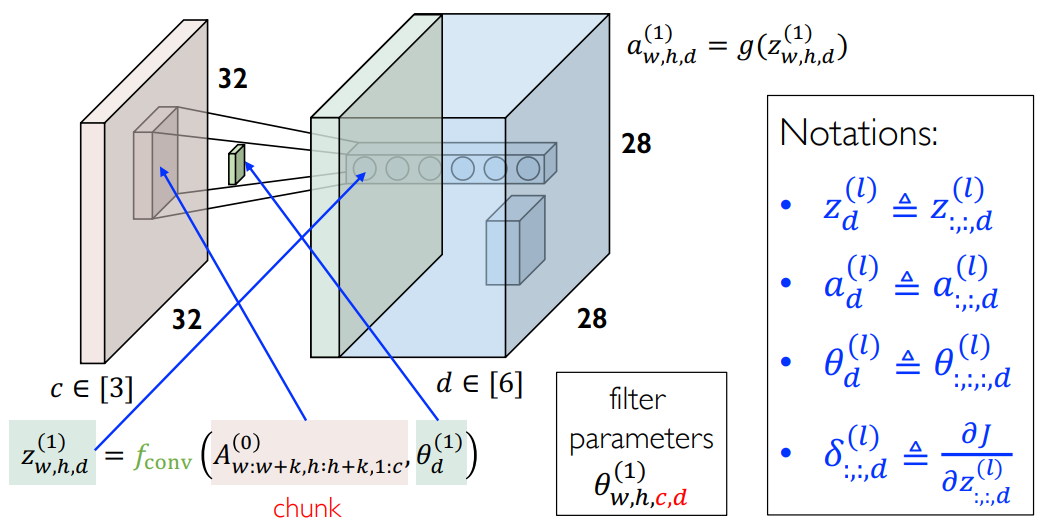
从
得到第一层第
把所有的激活值组合成一张特征图,再把所有的特征图组合起来得到新的 Volume:
对于:
:生成第 层需要的参数 :第 层特征图上结果所在的位置坐标 ,其实不重要 :输入通道数为 ,输出通道数为
因此有的时候也用:
表达整个第 个特征图/未激活前的特征图 表达激活后的特征图 表示第 个卷积核,它可以得到第 层的第 个特征图 是残差,表示损失函数值对 的偏导数
反向传播
首先我们考虑最简单的情况:输入是一通道,输出也是一通道:
展开为矩阵:
其实就是在
计算残差(目标函数对未激活值的导数):注意要用递推思想,将第
考虑第
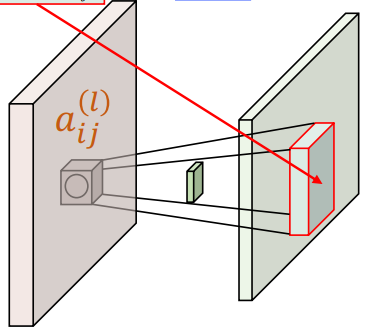
例如:左上角的
而对于中心的
因此有:
因此和全连接网络不同,