第二章 多层感知机

2.1 神经元与感知机

深度学习/神经网络的创立是受到了大脑神经元的启发，神经元由树突、轴突和神经末梢组成：

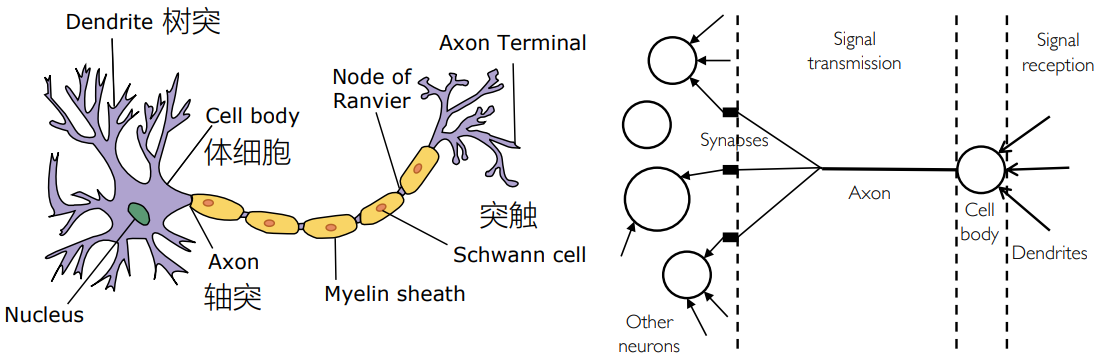
• 树突 dendrite：负责从其他神经元接收信号
• 体细胞 soma：处理信息
• 轴突 axon：发送信号
• 突触 synapses：连接轴突和树突的部分

人们将神经元抽象出来就得到了感知机 Perceptron 的数学模型，这个工作由心理学家 Rosenblatt 于 1958 提出：

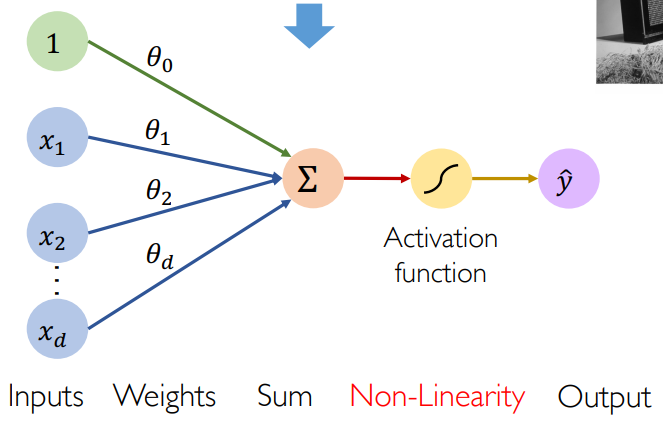
• 接收信息的部分：输入 inputs
• 处理信息的部分：线性组合 + 非线性映射/激活函数 activation function
• 发送信息的部分：输出 output

写出数学公式就是：

$$\hat{y}=g({\theta }_0+\sum _{i=1}^d{x}_i{\theta }_i)$$

感知机最重要的部分就是非线性的激活函数 $g$。如果没有这个非线性的激活函数，那么它就是输入的线性组合，对应的是高维空间中的一个超平面，并且带有截距。因此，感知机就是在超平面的基础上嵌入了一个非线性的激活函数。

那么什么是激活函数呢？回到仿生学的概念，对于大脑的神经元细胞来说，它往往有两个状态，一个是接收到信息的激活状态，还有就是没有接收到信息的非激活状态。一般来说会在信号达到某个强度/阈值的时候发生激活。因此 Rosenblatt 提出激活函数是符号函数，对应的输出公式就是：

$$\hat{y}=\text{sgn}(\sum _i{\theta }_i{x}_i-T)=\{\begin{array}{ll}1,& \text{if }{\displaystyle \sum _i{\theta }_i{x}_i-T⩾0}\\ 0,& \text{otherwise}\end{array}$$

Rosenblatt 对此很自信，认为感知机可以做任何事情！但图灵奖得主 Minsky 发现感知机（神经元/单元）能做的事情很少。显然，这种单元比大脑的神经元简单很多。

2.1.1 感知机学习算法

感知机学习算法 Perceptron Learning Algorithm，PLA 由 Marvin Minsky 和 Seymour Papert 于 1969 年提出。虽然它很简单，但是它却表示了深度学习算法的基本范式。注意到，激活函数是符号函数，它是一个不光滑的函数，因此不具有梯度性质，不能用基于梯度的方法求解：

• 输入：
  • $T_0$：迭代次数
  • ${\left\{({\mathit{x}}_i,y_i)\right\}}_{i=1}^m\subset {\mathbb{R}}^d\times \{-1,+1\}$：$m$ 个数据：每个数据是 $d$ 维输入向量和 $2$ 元输出向量
• 输出：
  • 训练结果：参数 $\mathit{\theta }$，线性组合的系数：表示不同维度的重要性
• 算法：
  • 初始化：${\mathit{\theta }}_0=0$
  • 进行 $t=1,\dots ,T_0$ 次迭代
  • 每次迭代取出训练集中的一条样本：$({\mathit{x}}_t,y_t)$
  • 将这条样本输入到感知机中计算结果：$\hat{y}=\text{sgn}({\mathit{x}}_t\cdot \mathit{\theta })$
  • 如果感知机的输出和真实值不同，即：$\hat{y}\ne y_t$，更新 $\mathit{\theta }=\mathit{\theta }+y_t{\mathit{x}}_t$，往错误方向更新
  • 否则保持 $\mathit{\theta }$ 不变

由于 $y\in \{-1,+1\}$，因此它只会让 $\mathit{\theta }$ 加减 $\mathit{x}$：

2.1.2 收敛率定理

定义 $\gamma$ 为最优间隔 the best-case margin：间隔指的是超平面和训练点之间的间距，那么最优间隔就是所有的这些间隔中的最小值。即：假设存在某个超平面的法向量 $\mathit{v}\in {\mathbb{R}}^d$，它可以满足对于任意训练点 $({\mathit{x}}_i,y_i)$ 都有：

$$\gamma \le \frac{y_i(\mathit{v}\cdot {\mathit{x}}_i)}{\parallel \mathit{v}\parallel }$$

定义 $R$ 是所有样本点的模的最大值，即：$R=max\{\parallel {\mathit{x}}_i\parallel \}$。

感知机的收敛率定理可以写为：感知机算法会在不超过 ${\left(\frac{R}{\gamma }\right)}^2$次迭代后收敛。同时也可以看出最优间隔 $\gamma$ 越大，迭代次数越少，收敛越快；样本点的模越大，训练点离原点越远，表明数据越分散，迭代次数越多，收敛越慢。如果一个问题是线性不可分的，那么无法找到超平面，无法收敛。

证明：

令 $I$ 为 $T$ 轮迭代中，那些有更新 $\mathit{\theta }$ 的迭代集合，记 $|I|=M$，也就是说，在 $T$ 轮迭代中一共更新了 $M$ 次。由此可以得到：

$$M\gamma \le \frac{\sum _{t\in I}{y}_t(\mathit{v}\cdot {\mathit{x}}_t)}{\parallel \mathit{v}\parallel }$$

• 不等式的左边：最优间隔 $\gamma$ 的 $M$ 倍
• 不等式的右边：集合 $I$ 中所有样本点到超平面 $\mathit{v}$ 的距离

根据 Cauchy-Schwarz 不等式：两个向量的内积小于等于各自模的乘积：

$$\frac{\sum _{t\in I}{y}_t(\mathit{v}\cdot {\mathit{x}}_t)}{\parallel \mathit{v}\parallel }=\frac{\mathit{v}}{\parallel \mathit{v}\parallel }\cdot \sum _{t\in I}{y}_t{\mathit{x}}_t\le \Vert \sum _{t\in I}{y}_t{\mathit{x}}_t\Vert$$

根据更新公式：${\mathit{\theta }}_{t+1}={\mathit{\theta }}_t+y_t{\mathit{x}}_t$ 可以得到：

$$\Vert \sum _{t\in I}{y}_t{\mathit{x}}_t\Vert =\Vert \sum _{t\in I}({\mathit{\theta }}_{t+1}-{\mathit{\theta }}_t)\Vert =\Vert {\mathit{\theta }}_{T+1}\Vert$$

改写裂项求和，但是用向量模的形式：

$$\Vert {\mathit{\theta }}_{T+1}\Vert =\sqrt{\sum _{t\in I}({\Vert {\mathit{\theta }}_{t+1}\Vert }^2-{\Vert {\mathit{\theta }}_t\Vert }^2)}=\sqrt{\sum _{t\in I}({\Vert {\mathit{\theta }}_t+y_t{\mathit{x}}_t\Vert }^2-{\Vert {\mathit{\theta }}_t\Vert }^2)}$$

再次使用更新公式，展开，同时注意到我们这里的 $I$ 是更新过参数的集合，也就是分类错误的集合，也就是说 $\text{sgn}(\mathit{\theta }t\cdot \mathit{x}t)\ne y_t$：

$$\sqrt{\sum _{t\in I}(\underset{\le 0}{\underbrace{2y_t{\mathit{\theta }}_t\cdot {\mathit{x}}_t}}+{\Vert {\mathit{x}}_t\Vert }^2)}\le \sqrt{\sum _{t\in I}{\Vert {\mathit{x}}_t\Vert }^2}\le \sqrt{M{R}^2}$$

因此有：

$$M\gamma \le \sqrt{M{R}^2}\Rightarrow M\le {\left(\frac{R}{\gamma }\right)}^2$$

也就是说，更新次数有上界，即算法会收敛。

2.1.3 布尔函数分析

人们首先研究感知机能否表达最简单的布尔函数集合：与或非。事实上，感知机可以表达与或非三种布尔函数，只是需要改变权重和激活函数的阈值：

• 与门：权重都为 1，阈值为 2，只有当输入都是 1 的时候才会被激活，输出 1
• 或门：权重都是 1，阈值为 1，只要有输入为 1 的的话，就会被激活，输出 1
• 非门：权重为 -1，阈值为 0：
  • 输入为 1，处理后为 -1，非激活状态，输出 0
  • 输入为 0，处理后为 0，激活状态，输出 1

啊哈，虽然它可以表示与或非这三种基本运算，但是感知机无法表达异或操作！为什么感知机无法表达异或操作？如下图所示：输入 X 和 Y 分别取 0 或 1 的时候输出为：

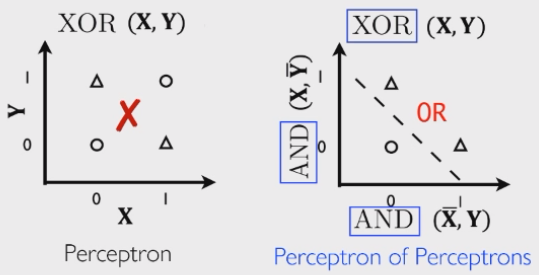
• 当 X 和 Y 都为 0 或 1 时，XOR(X,Y) = 0
• 当 X 和 Y 不同时，XOR(X,Y) = 1

它呈现了一种交叉状态，这种二分类问题感知机是无法做的 —— 因为本质上它是一个线性分类器。XOR 问题就是一个典型的线性不可分问题。但是！我们知道异或可以写成与或非的组合表达式。如上图所示：先画出 AND(~X, Y) 和 AND(X,~Y)，可以知道：

• AND(~X, Y)：当且仅当 X = 0，Y = 1 时输出为 1（左上角）
• AND(X, ~Y)：当且仅当 Y = 0，X = 1 时输出为 1（右下角）
• OR[AND(~X, Y), AND(X, ~Y)]：等价于 XOR(X, Y) 覆盖一下

单选题：关于感知机（Perceptron）：$\hat{y}=g({\theta }_0+\sum _{i=1}^d{x}_i{\theta }_i)$ 的以下描述中，正确的是？

• 一共有 $d$ 个可学习参数：错误，$d+1$ 个参数 ${\theta }_i$，包括截距
• 单个感知机就可以表达异或关系：错误，异或关系线性不可分
• 通过 $g$ 引入非线性之后，可以表达任意布尔逻辑：错误，$g$ 只是个函数，因此无法表达异或
• $g$ 为 Sigmoid 函数时，输出值 $\hat{y}$ 取值为 1 或 0：错误，范围是 $[0,1]$

2.2 多层感知机

既然说感知机只是一个神经元，而大脑中存在 ${10}^{11}$ 个神经元。模拟大脑，多层感知机 Multilayer Perceptron，MLP 就增加感知机的层数，一层一层连接起来，这里采用一种最简单的神经元连接方式：直接连接。

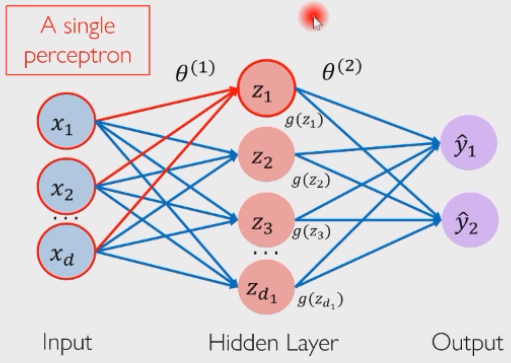
如图所示：我们数的层数其实是“箭头”，代表的变换层的个数，这里是一个两层的多层感知机。我们这个 $d$ 条红色的线标出来的就是一个感知机，一个感知机包括 $d$ 个输入，有 $d$ 条输入线。上图中第一层有 $d_1$ 个感知机，因为有 $d_1$ 个输出。第二层一共有两个感知机。

人脑中神经元是复杂网状结构连接的，不是这样分层连接的。感知机单元，以及单元之间的连接都太简单了，因此不能够模拟大脑。

2.2.1 多层感知机表达异或

异或的与或非表示：

$$X\oplus Y=(X\vee Y)\mathrm{\&}(\overline{X}\vee \overline{Y})$$

因此可以用三个感知机来表达异或：

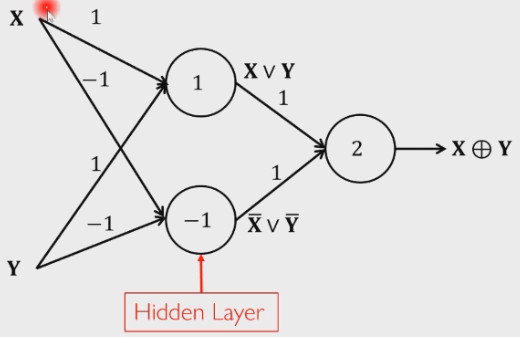
• 第一个感知机：权重为 1 和 1，阈值为 1
  • 当且仅当 X 和 Y 都为 0 时，输出为 0，其余都输出为 1
  • 表达了 X or Y
• 第二个感知机：权重为 -1 和 -1，阈值为 -1
  • 当且仅当 X 和 Y 都为 1 时，输出为 0，其余都输出为 1
  • 表达了 ~X or ~Y
• 隐藏层感知机：权重为 1 和 1，阈值为 2
  • 当且仅当输入都为 1 时，输出为 1，否则输出为 0
  • 表达了 AND 操作

如果你的目标函数可以写成简单的布尔运算复合表达式，那么可以用多层感知机表示。例如：

$$((A\mathrm{\&}\overline{X}\mathrm{\&}Z)\mid (A\mathrm{\&}\overline{Y}))\mathrm{\&}((X\mathrm{\&}Y)\mid \overline{(X\mathrm{\&}Z)})$$

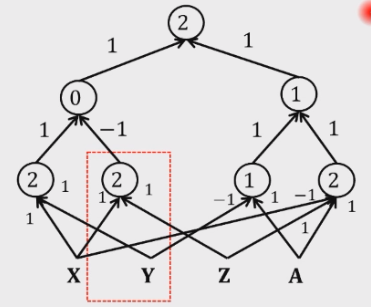
从左到右依次是：

• 输入层：
  • 权重：1 1，阈值：2。X and Y
  • 权重：1 1，阈值：2。X and Z
  • 权重：-1 1，阈值 1。~Y and A
  • 权重：-1 1 1，阈值 2。~X and Z and A
• 第二层：
  • 权重：1 -1，阈值：0。input1 or ~input2，即 (X & Y) | ~(X & Z)
  • 权重：1 1，阈值：1。input3 or input4，即 (~Y & A) | (~X & Z & A)
• 第三层：
  • 权重：1 1，阈值：2。input5 and input6，即 ((X & Y) | ~(X & Z)) & ((~Y & A) | (~X & Z & A))

注意到，上面这种多层感知机是稀疏 sparse 的。即每一个感知机只和前一层的有限个感知机连接。稀疏性是一个先验知识，在自然界中广泛存在，我们的大脑中的神经元也是一个稀疏连接的方式，因此称其为归纳偏好。

2.2.2 感知机表达实函数

感知机中的输入线性组合对应的就是高维空间中的超平面，然后再令激活函数为符号函数即可：

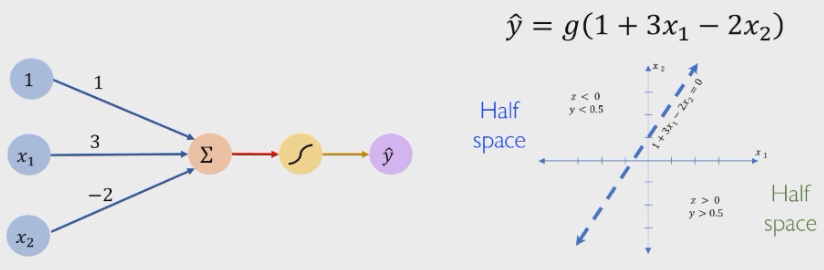
2.2.3 多层感知机表达复杂决策面

如何用多层感知机去刻画一个不规则的决策面？

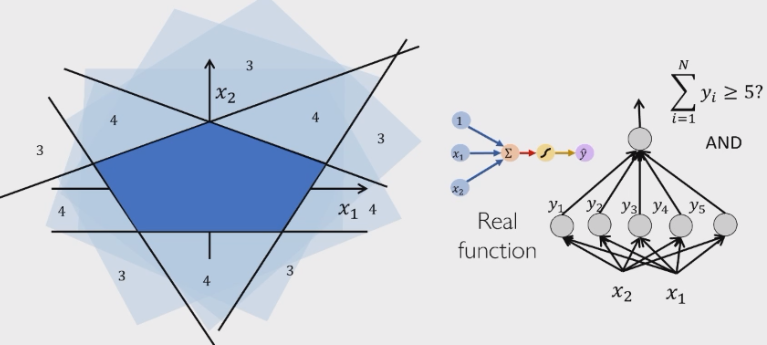
这是一个五边形，因此就是五个线性超平面包围而成：使用五个感知机，最后取一个与操作即可。其实一个两层感知机就可以用表达所有凸区域了。

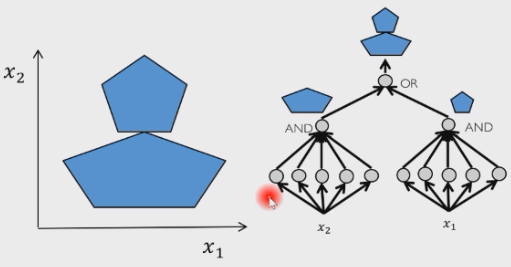
这里使用了一个三层的 MLP 网络表达了一个更复杂的决策面 —— 那么也许网络的深度决定了它的表达能力？经过多少次布尔变换复合就加多少层 MLP。但是可表达不意味着可学习：如图所示是可表达的情况，而可学习指的是存在一种学习算法可以找到最优参数，这涉及到数学上的困难。

2.3 神经网络

2.3.1 图形化多层感知机

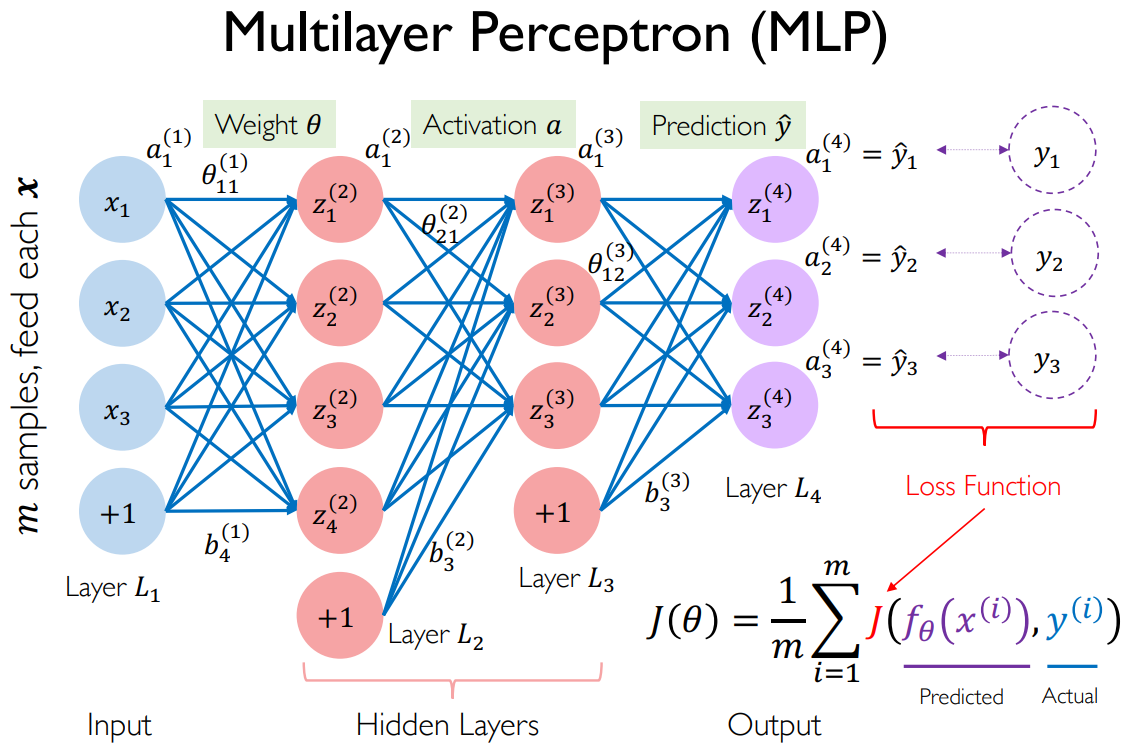
一般至少包含这么几层：

• 输入层：神经元个数固定，与问题有关
• 输出层：神经元个数固定，与输出标签数有关
• 隐藏层：自行确定神经元个数，同时有多少非线性变换就有多少连线
• 总参数量：边的条数

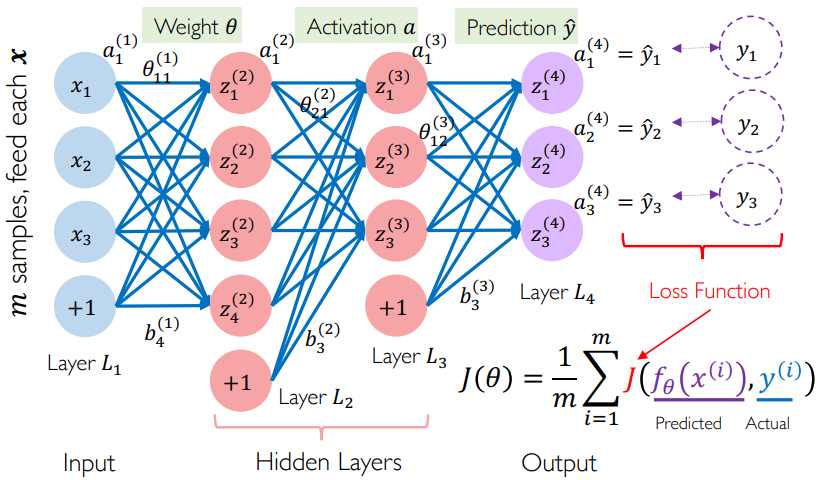
数学约定：

• 上标 $(k)$ 表示第 $k$ 层，下标 $i$ 表示第 $i$ 个神经元
• $z_i^{(k)}$ 表示第 $k$ 层的第 $i$ 个神经元，线性变换后的结果
• $a_i^{(k)}$ 表示 $z_i^{(k)}$ 经过非线性变换（激活函数）之后的结果
• ${\theta }_{ij}^{(k)}$ 表示第 $k$ 层变换中下一层的第 $i$ 个神经元和上一层的第 $j$ 个神经元之间的边的权重，也就是 $z_i^{(k+1)}$ 和 $a_j^{(k)}$ 连线的权重
• ${\hat{y}}_i$ 表示第 $i$ 个输出

$m$ 个训练样本的损失函数之和（训练误差）为：

$$J(\theta )=\frac{1}{m}\sum _{i=1}^{m}J(f_{\theta }\left(x^{(i)}\right),y^{(i)})$$

• $f_{\theta }\left(x^{(i)}\right)$：预测值
• $y^{(i)}$：真实值
• $f_{\theta }$：一个抽象函数，代表感知机网络表达的函数

2.3.2 隐藏层的激活函数

通过激活函数 Activation Function 决定非线性性质：$\hat{y}=g({\theta }_0+{\mathit{X}}^T\mathit{\theta })$：

在深度学习的发展历程中，人们一开始选择了 Sigmoid 函数作为激活函数：它的优点是可以将负无穷到正无穷的值映射到 $[0,1]$ 之间，从而具有某种概率上的含义。机器学习中就使用了 sigmoid 函数做逻辑斯蒂回归。防止出现连乘爆炸现象，考虑 [0,1] 之间的函数。但是这种激活函数某种程度上阻碍了神经网络 30 年的发展 —— 梯度消失 Gradient Saturation 现象。

$$g(z)=\sigma (z)=\frac{1}{1+e^{-z}}$$

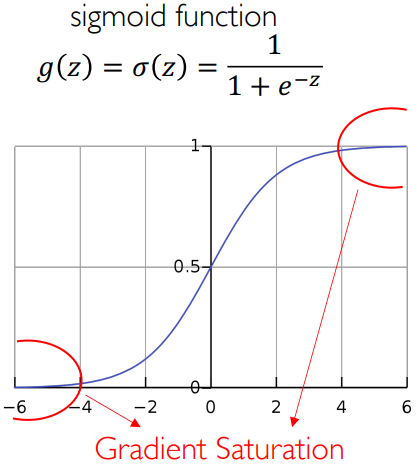
人们一直使用 Sigmoid 函数以及双曲正切函数作为激活函数，考察它们的函数及其导数图像：

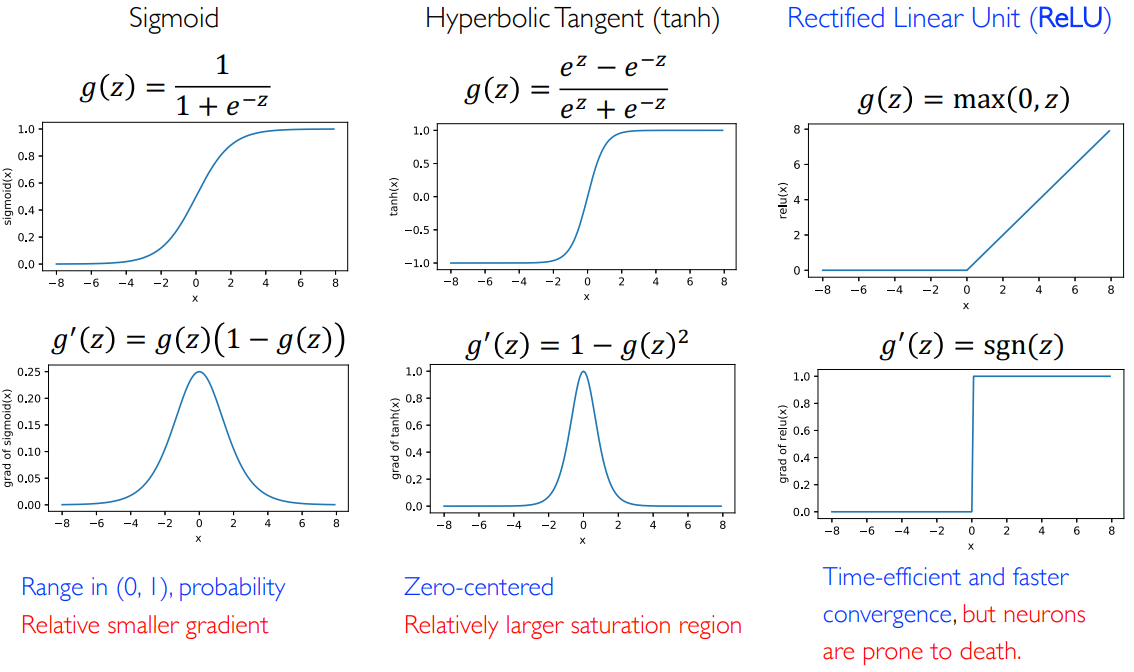
可以看到，当数值太大时，激活函数的导函数变为零（导数性质很差），而梯度饱和/梯度消失指的是：当输入太大了就会进入饱和区，此时用基于梯度的求解方式，如 SGD，就会没有梯度，而没有梯度就没有优化方向了，就没法继续做了。

一直到 2010 年人们才意识到这一点，因此 Hinton 于 2010 年提出了整流线性函数 Rectified Linear Unit，ReLU，并使其获得了图灵奖。ReLU 函数不存在梯度消失现象，因此 ReLU 函数的提出标志着神经网络训练的实用化，可以训练多层神经网络了。

一直到 2010 年人们才意识到这一点，因此 Hinton 于 2010 年提出了整流线性函数 Rectified Linear Unit，ReLU，并使其获得了图灵奖。ReLU 函数不存在梯度消失现象，因此 ReLU 函数的提出标志着神经网络训练的实用化，可以训练多层神经网络了。

我们给出饱和的数学定义：对于函数 $g$，如果对于输入 $z$， $\underset{z\to \mathrm{\infty }}{lim}|\mathrm{\nabla }g(z)|=0$ 。不饱和的激活函数就不会受到梯度消失的影响，梯度消失会使得网络无法更新，因此一定要选择不饱和的激活函数！在 2016~2017 年人们提出了高斯误差激活单元 Gaussian Error Linear Unit，GELU：

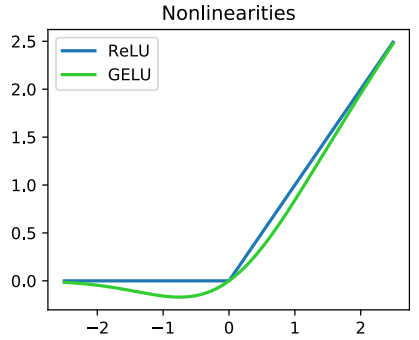
GELU 和 ReLU 的区别在于它在负数的时候仍然有梯度，ReLU 在大于 0 的时候梯度是 1，小于 0 的时候梯度是 0（杀死了一半的输入），GELU 则不会，因此进一步提高了可表达能力。GELU 被广泛应用于高级复杂模型，如 GPT-3，BERT 和 Transformer。

GELU 使用百分位数对权重进行加权：

$$\text{GELU}(z)=zP(Z⩽z)=z\mathrm{\Phi }(z)=z\cdot \frac{1}{2}[1+\text{erf}\left(\frac{z}{\sqrt{2}}\right)],Z\sim \mathcal{N}(0,1)$$

而 ReLU 其实就是没有进行加权：

$$\text{ReLU}(z)=z\mathbf{1}[z\ge 0]$$

其他关于 GELU 的性质可以参考：https://en.wikipedia.org/wiki/Activation_function

2.3.3 输出层的激活函数

输出层也需要一个激活函数，将 $z$ 变换为 $a=y$，作为输出值。输出层的激活函数由问题决定：

• 如果问题的真实值是连续值，那么输出值不需要激活函数，即采用线性函数。
• 如果问题是回归问题但有界，可以采用 sigmoid 或 tanh 作为激活函数，使输出值有界。
• 如果问题是多分类问题，真实值是标签，那么就需要使用到 Softmax 激活函数。

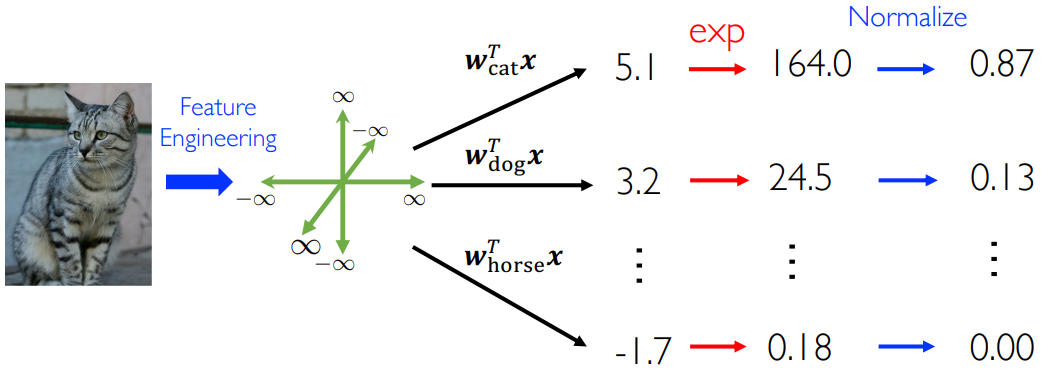
多分类问题：给定一个输入数据，得到多个输出，代表多个标签，但是不同标签对应的概率也不一样。例如一幅画中有猫狗和驴子，但是占比不同，现在要输出画的内容标签，因此不同标签对应的概率也不同。

建立分类问题的简单数学模型：基于骰子，骰子可以看作是一个六输出的模型，并且每次标签的概率为 1/6。这就是分类问题的随机试验。考虑这样一个问题：如果这个网络有 $k$ 个输出 $z_1,\cdots ,z_k$，怎么将它们变成一个 0~1 之间的概率：

• 取指数：$z_i\to e^{z_i}$ 可以将 $z_i$ 映射到 $[0,+\mathrm{\infty })$
• 归一化：得到 0~1 上的概率
• 最终将 $[-\mathrm{\infty },+\mathrm{\infty }]$ 上的 $k$ 个输出变成 $[0,1]$ 上的 $k$ 个概率，并且它们之和为 1
• 当然有其他的方法可以完成上述操作，但是人们选了一个性质最好的：

$$g(\mathit{z}{)}_i=\frac{e^{z_i}}{\sum _{j=1}^k{e}^{z_j}}$$

只与为什么叫 Softmax 函数，因为它和普通的 $max$ 函数有较大区别，例如：

$max\{-2,1,5\}=5$，它直接丢弃了 -2 和 1 这两个数，而 Softmax 则是通过指数函数，拉开 -2、1 和 5 之间的差距，最后归一化输出概率。如果是 4 和 5 的话，输出的概率分别为 0.27 和 0.73。

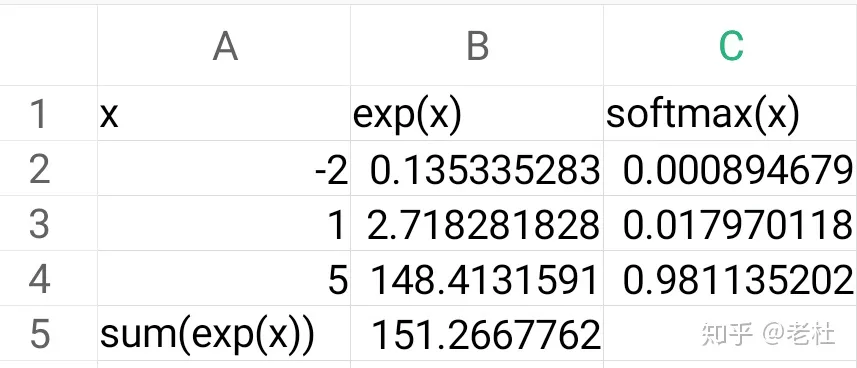
当然这个函数也有一些问题：

• 赢者通吃：如果某个 $z_i$ 比较大，那么它对应的指数就会特别大（指数无法正确反映实际 $z$ 值的差距），导致 Softmax 的结果一般都是单峰的。这会导致深度学习中产生过度自信 OverConfidence 的情况，即实际上没有那么大的概率。
• 数值不稳定：$z$ 经过指数函数容易溢出。实际实现，先除以指数函数中的最大值：此时所有指数函数的值都小于 1，不会出现上溢出，这是一个计算机技巧。

$$g(\mathit{z}{)}_i=\frac{e^{z_i-z_u}}{\sum _{j=1}^k{e}^{z_j-z_u}},u={\text{argmax}}_j\left(z_j\right)$$

多重伯努利分布 Categorical Distribution：$k$ 个位于 $[0,1]$ 之间的数，同时和为 1：

$$z_j\in (-\mathrm{\infty },+\mathrm{\infty })\Rightarrow {\hat{y}}_j\in [0,1],\sum _{j=1}^k{\hat{y}}_j=1$$

2.3.4 交叉熵损失函数

Softmax 函数在输出层的表示：

$$\hat{\mathit{y}}={\mathit{a}}^{\left(n_l\right)}=f_{\theta }\left({\mathit{x}}^{(i)}\right)=\left[\begin{array}{c}p(y^{(i)}=1\mid {\mathit{x}}^{(i)};\mathit{\theta })\\ p(y^{(i)}=2\mid {\mathit{x}}^{(i)};\mathit{\theta })\\ ⋮\\ p(y^{(i)}=k\mid {\mathit{x}}^{(i)};\mathit{\theta })\end{array}\right]=\frac{1}{\sum _{j=1}^k\exp \left(z_j^{\left(n_l\right)}\right)}\left[\begin{array}{c}\exp \left(z_1^{\left(n_l\right)}\right)\\ \exp \left(z_2^{\left(n_l\right)}\right)\\ ⋮\\ \exp \left(z_k^{\left(n_l\right)}\right)\end{array}\right]$$

第 $i$ 个数据 ${\mathit{x}}^{(i)}$ 经过以 $\mathit{\theta }$ 为参数的网络，输出的结果就是 $\hat{\mathit{y}}$，本来网络输出的是 $k$ 个 $z$，经过 Softmax 这一输出层函数之后变成了 $k$ 个 $y$，成了概率。其中 $n_l$ 为网络层数。最终得到的向量是一个条件概率向量。

那么如何刻画预测值 $\hat{\mathit{y}}$ 与真实值 $y$ 之间的差异呢？首先可以把真实值 $y$ 改写为独热向量 one-hot coding：当 $y$ 为第 $j$ 类时，有 $\mathit{y}:y_j=1,y_i=0(i\ne j)$。那么可以采用一范数、二范数、MSE 等等来刻画差异。在深度学习中，我们使用交叉熵 Cross-entropy 来刻画损失函数（由极大似然估计推导而来）：

$$J(\mathit{q},\mathit{p})=-\sum _{j=1}^k{q}_j\log p_j,J(\mathit{y},\hat{\mathit{y}})=-\sum _{j=1}^k{y}_j\log {\hat{y}}_j$$

交叉熵主要用于刻画两个多分类分布 $\mathit{q}$ 和 $\mathit{p}$ 的距离。真实值和预测值不要弄反，是 $\log \hat{y}$！写开来，得到：

$$\underset{\theta }{min}J(\theta )=-\frac{1}{m}\sum _{i=1}^m[\sum _{j=1}^k\mathbf{1}\{y^{(i)}=j\}\log \frac{\exp \left(z_j^{\left(n_l\right)}\right)}{\sum _{j^{\prime }=1}^k\exp \left(z_{j^{\prime }}^{\left(n_l\right)}\right)}]$$

其实这个式子很少，只有 $m$ 项作了求和。

这里再解释一下 ${\mathit{y}}^{(i)}$ 和 $y^{(i)}$ 的区别，对于每一个输入数据 ${\mathit{x}}^{(i)}$，都有唯一一个标签 $y^{(i)}=j$，但我们将它写成独热标签的形式，也就是 ${\mathit{y}}^{(i)}$ 是只有第 $j$ 行为 1，其余行为 0 的 $k$ 维向量，即：

$$\mathbf{1}\{y^{(i)}=j\}=\{\begin{array}{ll}1,& y^{(i)}=j\\ 0,& \text{otherwise}\end{array}$$

所谓独热标签，实际上就是表示类别的一种方法。对于 $k$ 类，可以用 $y=1,2,\cdots ,k$ 表示类别归属，也可以用 $\mathit{y}=[0,1,0,\cdots ,0{]}^T$ 来表示 $y$ 属于第二类。

多选题：以下描述中，正确的是？

• 激活函数中，Sigmoid 和 ReLU 都可能梯度饱和：错误，ReLU 不会
• Softmax 具有赢者通吃的特点：正确，指数函数放缩值太大
• 为了避免数值溢出，Softmax 通常先除以最大值：正确
• MLP 可以用感知机学习算法求解：错误，要用反向传播算法

2.4 软最大回归

软最大回归 Softmax Regression 实际上是一个多分类模型。我们现在有多个类别，我们希望能够预测出输入属于每一个类别的概率：

• 首先我们要找到 $k$ 个分类超平面：${\mathit{w}}_1,{\mathit{w}}_2,\cdots ,{\mathit{w}}_k$ 作为法向量来表示
• ${\mathit{w}}_i^T\mathit{x}$ 负责输出 $\mathit{x}$ 隶属于第 $i$ 类的可能性，注意这里的可能性是一个 $[-\mathrm{\infty },+\mathrm{\infty }]$ 上的数 score
• 直观来看，应该是靠近其他分类点的超平面
• 给可能性分数归一化，得到 [0,1] 上的概率：Softmax 函数
• 其实，可能性分数无非就是人们不知道如何处理多维的特征输入了，那就直接线性组合吧！

公式为：

$$p(y=j\mid \mathit{x};\mathit{W})=\frac{\exp \left({\mathit{w}}_j^{\mathsf{T}}\mathit{x}\right)}{\sum _{j^{\prime }=1}^k\exp \left({\mathit{w}}_{j^{\prime }}^{\mathsf{T}}\mathit{x}\right)}$$

一个直观的图像分类例子给出多分类模型的原理：

2.4.1 统计观点

软最大回归是一个很自然的想法。他的随机试验模型为：扔骰子/多项分布：

$$P(y=j\mid \mathit{q})=q_j,\mathit{q}\in {\mathbb{R}}^k,\sum _{j=1}^k{q}_j=1$$

上式表示在分布 $\mathit{q}$ 的意义下，事件 $y=j$ 发生的概率为 $q_j$。若一共扔了 $m$ 次独立同分布的骰子，考虑第 $i$ 次骰子第 $j$ 面朝上的概率为（注意这里不一定要求骰子是均匀的）：$q_{ij}$。重复 $m$ 次后得到的结果为 $\{y_1,y_2,\cdots ,y_m\}$，即：

$$P(y=j\mid \mathit{q})=q_j,\mathit{q}\in {\mathbb{R}}^k,\sum _{j=1}^k{q}_j=1$$

• 首先，独立重复了 $m$ 次，因此利用独立事件发生的乘法原理，连乘 $m$ 次
• 其次，每次试验有 $k$ 种结果，每个结果出现的概率为 $P(y_i=j\mid q_{ij})$
• 最后，示性函数 $\mathbf{1}\{y_i=j\}$ 表示了该结果 $y_i=j$ 是否出现，出现则乘 $p$，不出现则乘 $1$
• 很多独立同分布重复实验都是这样写的

软最大回归做的假设为：分布 $\mathit{q}$ 可以用 Softmax 函数族来进行逼近：

$$q_{ij}=P(y_i=j\mid {\mathit{x}}_i;\mathit{W})$$

代入公式中，得到参数 $\mathit{W}$ 在样本集 $\mathcal{D}=\{({\mathit{x}}_i,y_i){\}}_{i=1}^m$ 上的似然函数（以参数化模型表达出样本集的可能性）为：

$$\mathcal{L}(\mathit{W};\mathcal{D})=\prod _{i=1}^m\prod _{j=1}^{k}P{(y_i=j\mid \mathit{x}\ast i;\mathit{W})}^{\mathbf{1}\{y\ast i=j\}}$$

极大似然估计：

$$\mathcal{L}(\mathit{W};\mathcal{D})=\underset{{\mathit{w}}_1,\dots ,{\mathit{w}}_k}{max}\prod _{i=1}^m\prod _{j=1}^{k}P{(y_i=j\mid {\mathit{x}}_i;\mathit{W})}^{\mathbf{1}\{y_i=j\}}$$

这里出现了两个连乘，数值上会溢出，因此我们做最小负对数似然估计：

$$\mathcal{L}\mathcal{L}(\mathit{W};\mathcal{D})=\underset{{\mathit{w}}_1,\dots ,{\mathit{w}}_k}{min}-\frac{1}{m}\sum _{i=1}^m\sum _{j=1}^k\{\mathbf{1}\{y_i=j\}\cdot \log P(y_i=j\mid {\mathit{x}}_i;\mathit{W})\}$$

取 $1/m$ 也是担心数据溢出，最后将 Softmax 函数带入参数化模型中：

$$\mathcal{L}\mathcal{L}(\mathit{W};\mathcal{D})=\underset{{\mathit{w}}_1,\dots ,{\mathit{w}}_k}{min}-\frac{1}{m}\sum _{i=1}^m\sum _{j=1}^k\{\mathbf{1}\{y_i=j\}\cdot \log \frac{\exp ({\mathit{w}}_j^T{\mathit{x}}_i+{\mathit{b}}_j)}{\sum \ast {j^{\prime }=1}^k\exp ({\mathit{w}}_{j^{\prime }}^T{\mathit{x}}_i+{\mathit{b}}_{j^{\prime }})}\}$$

这竟然和交叉熵的损失函数完全一样！因此一句话总结软最大回归：就是认为分类问题是一个多重伯努利试验，然后使用 Softmax 函数对概率进行参数化建模，之后对参数做最大似然估计，得到的结果。因为这个过程是最合理的，最自然的 —— 如非必要，勿增实体。

SVM 等模型我们在深度学习中都不会使用，因为我们发现：只要你的函数族足够丰富，就可以在神经网络中对多重伯努利分布（以及其他任何分布）做一个准确的逼近。别的损失函数都是为了弥补函数族，因此深度学习的本质：找到某一个足够丰富的函数族，来对任意分布做参数估计。

为什么不叫软最大分类，而叫软最大回归呢？因为回归方程就是条件概率分布的期望 $\mathit{q}$，而使用了 Softmax 函数做回归方程的逼近，因此也被称为 Softmax 回归。

2.4.2 常见的损失函数

一些常见的损失函数：https://en.wikipedia.org/wiki/Cross_entropy

吉布斯熵函数 Entropy：

$$H(q)=-\sum _{j=1}^k{q}_j\log q_j$$

• 对一个 $q$ 有 $k$ 种不同取值
• 那么用多少比特数可以编码这个 $q$ 的信息
• 强化学习中的最大熵原理、自监督学习

相对熵，KL 散度：

$$\mathrm{KL}(q\parallel p)=-\sum _{j=1}^k{q}_j\log p_j-H(q)$$

• 在给定分布 $q$ 的情况下，还需要多少信息才可以编码分布 $p$，$p$ 和 $q$ 有关

交叉熵：

$$H(q,p)=-\sum _{j=1}^k{q}_j\log p_j$$

• 在多重伯努利试验中，结果的最大似然估计值就是一个交叉熵

交叉熵、相对熵和吉布斯熵之间的关系：

$$H(q,p)=\mathrm{KL}(q\parallel p)+H(q)$$

2.5 反向传播算法

基本上所有国外的优秀课程都细讲了反向传播算法求解，MLP 和 CNN 都讲了，吴恩达 Andrew Ng 还要求用 Matlab 实现，培养扎实的深度学习功底。

一些关键的概念 notations，需要再说明一下：下面是一个元素：

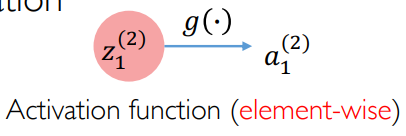
• $g$：激活函数，它是一个逐元素的函数
• $z$：激活前的元素，经过了线性组合
• $a$：激活后的元素，经过了非线性变换，也称为神经元的输出
• 上标 $(l)$ 表示第 $l$ 层，下标 $i$ 表示这一层的第 $i$ 个神经元
• $a_i^{(1)}=x_i$：第一层的输出和输入是相等的
• 第 $l$ 层的第 $i$ 个激活前元素 $z_i^{(l)}$，由第 $l-1$ 层所有激活后元素 $a_j^{(l-1)}$ 线性组合（一共 $s_{l-1}$ 个） + 截距 $b_i^{l-1}$（截距每个单元都不一样，也可以理解为 $b_i^{l-1}\cdot 1$）生成。层数 $l$：从 $2$ 开始，到 $n_l$ 结束：

$$z_i^{(l)}=\sum _{j=1}^{s_{l-1}}{\theta }_{ij}^{(l-1)}{a}_j^{(l-1)}+b_i^{(l-1)}$$

• $a_i^{(l)}=g\left(z_i^{(l)}\right)$ ：第 $l$ 层第 $i$ 个激活后元素，由非线性变换而来
• ${\hat{y}}_i=a_i^{\left(n_l\right)}$ ：最后一层的输出就是第 $n_l$ 层的输出

图示：

2.5.1 基于梯度的训练方法

待求解问题：

$$\underset{\theta }{\arg min}O(\mathcal{D};\theta )=\sum _{i=1}^{m}L(y_i,f\left(x_i\right);\theta )+\mathrm{\Omega }(\theta )$$

迭代算法：

• 函数值的前向传播：ForwardPropagation()
• 误差值的反向传播：BackwardPropagation()
• ${\theta }^{(t+1)}\leftarrow {\theta }^{(t)}-\eta {\mathrm{\nabla }}_{\theta }O(\mathcal{D};{\theta }^{(t)})$

如何求参数 $\mathit{\theta }$ 的梯度？注意目标函数和参数 $\mathit{\theta }$ 之间的关系是间接的 —— 链式求导。只有最后一层不需要使用链式求导法，因此我们先求最后一层。以多分类的 Softmax 输出函数为例，对于第 $i$ 个样本 $(x^{(i)},y^{(i)})$，对数损失函数为：

$$J(\theta ,b;x^{(i)},y^{(i)})=-\sum _{j=1}^k\mathbf{1}\{y^{(i)}=j\}\log \frac{\exp \left(z_j^{\left(n_l\right)}\right)}{\sum _{j^{\prime }=1}^k\exp \left(z_{j^{\prime }}^{\left(n^{\prime }\right)}\right)}$$

因此偏导数为（这个已验算，log-分式的链式求导即可，把示性函数看作系数）：

$$\frac{\partial J(\theta ,b)}{\partial z_j^{\left(n_l\right)}}=-(\mathbf{1}\{y^{(i)}=j\}-p(y^{(i)}=j\mid x^{(i)};\theta ))$$

这个梯度很简单，将真实概率值 - 预测概率值作为梯度方向！问题在于：为什么需要这个梯度呢？

对于其他层的损失函数：

$$J(\theta ,b)=\frac{1}{m}\sum _{i=1}^{m}J(\theta ,b;x^{(i)},y^{(i)})$$

梯度下降法更新各参数/截距的公式如下：

对于参数 $\mathit{\theta }$，第 $l+1$ 层第 $i$ 个神经元和第 $l$ 层第 $j$ 个神经元之间的参数 ${\theta }_{ij}^{(l)}$ 更新方式为：

$${\theta }_{ij}^{(l)}={\theta }_{ij}^{(l)}-\eta \frac{\partial }{\partial {\theta }_{ij}^{(l)}}J(\theta ,b)$$

偏导数为：

$$\frac{\partial }{\partial {\theta }_{ij}^{(l)}}J(\theta ,b)=\frac{1}{m}\sum _{i=1}^m\frac{\partial }{\partial {\theta }_{ij}^{(l)}}J(\theta ,b;x^{(i)},y^{(i)})$$

同理对于第 $l+1$ 层第 $i$ 个神经元的截距 $b_i^{(l)}$ 也有：

$$b_i^{(l)}=b_i^{(l)}-\eta \frac{\partial }{\partial b_i^{(l)}}J(\theta ,b)$$

写开了就是：

$$\frac{\partial }{\partial b_i^{(l)}}J(\theta ,b)=\frac{1}{m}\sum _{i=1}^m\frac{\partial }{\partial b_i^{(l)}}J(\theta ,b;x^{(i)},y^{(i)})$$

2.5.2 前向传播

我们先假设网络中所有的参数都是已知的，如果不知道就随机初始化，因为最后是要用梯度下降法不断地修改参数。传入输入数据，得到输出数据。前向传播干的事情：算出输出值在每一层的激活值。已经训练好的模型在做推理的时候本质上就是一个前向传播。

2.5.3 反向传播

把误差反向传播回去，看看每一层对错误的负责程度，损失函数对哪一层的梯度大，那么那一层负责程度大。

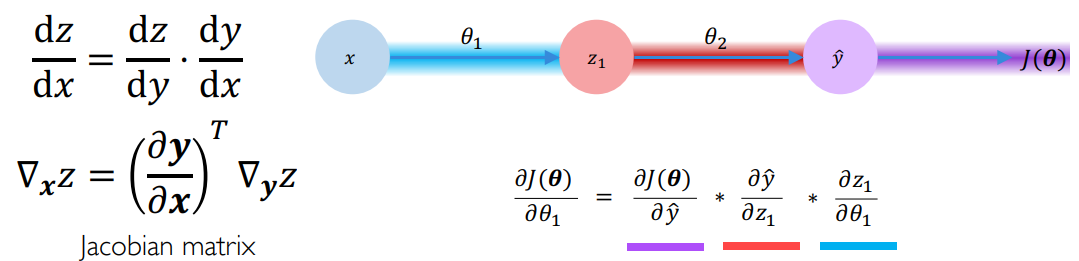
如图所示是一个两层的 MLP：

$$\frac{\partial J(\mathit{\theta })}{\partial {\theta }_1}=\frac{\partial J(\mathit{\theta })}{\partial \hat{y}}\ast \frac{\partial \hat{y}}{\partial z_1}\ast \frac{\partial z_1}{\partial {\theta }_1}$$

注意：在这个公式中，除了你要算的那个 $\theta$ 之外，别的层都是计算对于输出的导数！千万不要写成 $y$ 对 ${\theta }_2$ 的导数，之后就无法计算 $y$ 对 ${\theta }_1$ 的导数了。

反向传播算法是一个对链式法则的高效实现：

• 本质上是一个动态规划算法
• 避免重复计算子结构，保存起来，查表
• 用空间换时间，内存占用大，空间复杂度与样本条数/梯度信息成正比
• 本质上计算 $J$ 对每一层输出的导数，填表

所以反向传播算法的空间复杂度很高，所以显卡大是为了什么？为了提高显存，装下更多的样本。因此我们接下来要做的事就是求 $J$ 对每一层输出的导数，直到要求的那一层再换成求对于参数的导数即可：

2.5.4 残差计算

对于第 $l$ 层的节点 $i$，计算它对未激活输出 $z_j^{(l)}$ 的残差 residual：${\delta }_i^{(l)}$：

$${\delta }_i^{(l)}\triangleq \frac{\partial }{\partial z_i^{(l)}}J(\theta ,b;x,y)$$

也可以用 $a_i^{(l)}$，但是不够漂亮。${\delta }_i^{(l)}$ 刻画的是第 $l$ 层的节点 $i$ 对最后的错误 $J(\theta ,b)$ 责任的大小。也就是输出值 $z_j^{(l)}$ 的微小变化引起错误的多少微小的变化。

对于最后一层来说，残差为：

$${\delta }_i^{\left(n_l\right)}=\frac{\partial }{\partial z_i^{\left(n_l\right)}}J(\theta ,b;x,y)=\frac{\partial }{\partial \hat{y}i}J(\theta ,b;x,y)g^{\prime }\left(z{i}^{\left(n_l\right)}\right)$$

上面这个式子是可以计算的，因为损失函数是定义在预测值 $\hat{\mathit{y}}$ 上的，同时输出层的激活函数也是直到的。因此可以求出残差结果。

对于隐藏层呢？首先，每一个未激活的值都是上一层的神经元输出的线性组合：

$$z_j^{(l+1)}=\sum _{i=1}^{s_l}{\theta }_{ji}^{(l)}{a}_i^{(l)}+b_j^{(l)}$$

考虑残差关系，即下一层的每个未激活值 $z_j^{(l+1)}$ 都受到了上一层某个特定值 $z_i^{(l)}$ 的影响，因为这是一个全连接网络，画出图示为：

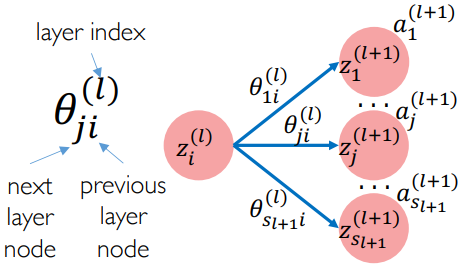
也就是说下一层的每个未激活值 $z_j^{(l+1)}$ 都是 $z_i^{(l)}$ 的函数，即：$z_j^{(l+1)}=f_j(z_i^{(l)}),j=1,2,\cdots ,s_{l+1}$，此时根据多元函数求导的链式法则可知（不需要线性都可以），由全微分的定义：

$$\mathrm{d}J=\sum _{j=1}^{s_{l+1}}\frac{\partial J}{\partial z_j^{(l+1)}}\mathrm{d}{z}_j^{(l+1)}$$

因此：

$$\frac{\partial J(\theta ,b;x,y)}{\partial z_i^{(l)}}=\sum _{j=1}^{s_{l+1}}\frac{\partial J(\theta ,b;x,y)}{\partial z_j^{(l+1)}}\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}$$

回顾线性组合公式：

$$z_j^{(l+1)}=\sum _{i=1}^{s_l}{\theta }_{ji}^{(l)}{a}_i^{(l)}+b_j^{(l)}$$

得到残差的递推公式为：

$${\delta }_i^{(l)}=\sum _{j=1}^{s_{l+1}}{\delta }_j^{(l+1)}{\theta }_{ji}^{(l)}{g}^{\prime }\left(z_i^{(l)}\right)$$

可以看到残差代表的错误信号从下一层反向传播回来了/递推回来了。但是我们注意到，残差是目标函数对输出的导数，而不是我们所关注的对参数的导数。

根据正向传播公式：

$$z_j^{(l+1)}=\sum _{i=1}^{s_l}{\theta }_{ji}^{(l)}{a}_i^{(l)}+b_j^{(l)}$$

可以求出对参数的导数：

$$\frac{\partial }{\partial {\theta }_{ij}^{(l)}}J(\theta ,b;x,y)=\frac{\partial }{\partial z_i^{(l+1)}}J(\theta ,b;x,y)\frac{\partial z_i^{(l+1)}}{\partial {\theta }_{ij}^{(l)}}=a_j^{(l)}{\delta }_i^{(l+1)}$$

因为 $z_i^{(l+1)}$ 本质上是 ${\theta }_{ji}^{(l)}$ 的函数。同时注意，这里面是没有对所有的 $z^{(l+1)}$ 节点求偏导数后求和，而是只对 $z_i^{(l+1)}$ 求了偏导数，因为 $z^{(l+1)}$ 对 ${\theta }_{ji}^{(l)}$ 的依赖只有一次（也就是正向传播公式），或者说第 $l+1$ 层节点中只有 $z_i^{(l+1)}$ 是 ${\theta }_{ji}^{(l)}$ 的函数，而不是所有第 $l+1$ 层节点都是它的函数（其余的节点关于它的偏导数都为 0）。

同理，计算截距对参数的导数为：

$$\frac{\partial }{\partial b_i^{(l)}}J(\theta ,b;x,y)=\frac{\partial }{\partial z_i^{(l+1)}}J(\theta ,b;x,y)\frac{\partial z_i^{(l+1)}}{\partial b_i^{(l)}}={\delta }_i^{(l+1)}$$

总结：目标函数对隐藏层参数的导数就是这一层节点的激活值乘上下一层节点的残差值。前向传播算出激活值，反向传播算出残差值，二者相乘就是梯度。

我们平时去改进一个优化算法，其实改进的是梯度优化，而不是改进前向传播算法和反向传播算法，反向传播算法只是用来计算残差的一个动态规划算法，是计算梯度的一个工具。

多选题 2：关于反向传播算法的描述中，正确的是？

• 使用链式法则计算每一层参数的梯度。
• 通常利用动态规划来避免梯度的重复计算。
• 计算第 $l$ 层残差项时，对第 $l+1$ 层残差项加权平均：错误，加权求和而不是加权平均。
• 上一项中的加权系数总为正数：错误，系数 ${\theta }_{ji}^{(l)}{g}^{\prime }\left(z_i^{(l)}\right)$ 不一定为正数。

2.5.5 自动求导

三种不同的数值微分方法：

符号方法：

$$\frac{\mathrm{d}(fg)}{\mathrm{d}x}=\frac{\mathrm{d}f}{\mathrm{d}x}g+f\frac{\mathrm{d}g}{\mathrm{d}x}$$

• 优点：无
• 缺点：推导复杂；容易推导出很多复杂的中间结构

数值方法：

$$\frac{\partial f(x)}{\partial x_i}\approx \underset{h\to 0}{lim}\frac{f(x+h{e}_i)-f(x-h{e}_i)}{2h}$$

• 优点：简单，可以检查自动求导方法是否错误
• 缺点：有截断误差，计算非常慢

反向传播：

• 优点：易于理解和实践
• 缺点：内存占用多，考虑优化调度，例如哪些需要先算

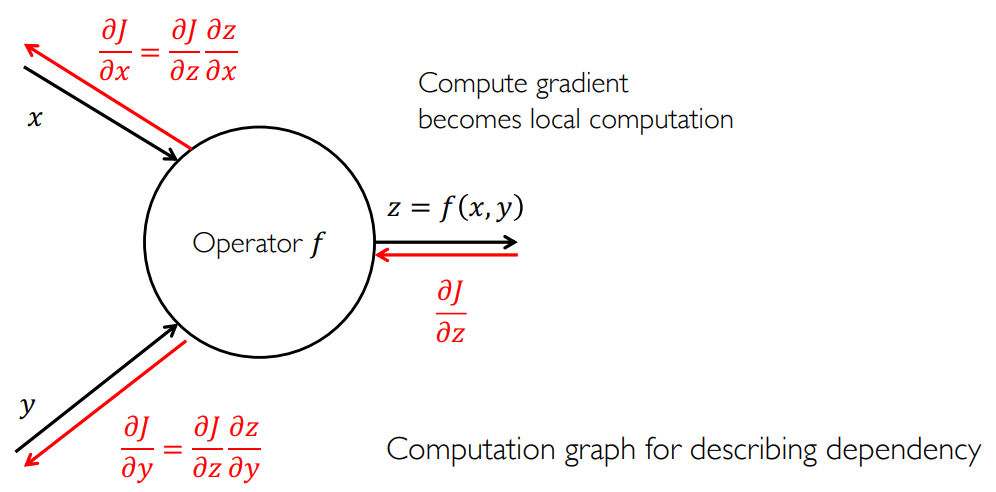
如图所示是一个 BP 算子。算子 $f$ 的输入是 $x$ 和 $y$，输出是 $z$，即 $z=f(x,y)$。后面有一个函数 $J$ 是以 $z$ 为自变量。那么现在要求 $J$ 对 $x$ 和 $y$ 的导数，需要先把目标函数 $J$ 关于输出 $z$ 的导数求出来，之后再求其对输入 $x$ 和 $y$ 的导数。即：

$$\frac{\partial J}{\partial x}=\frac{\partial J}{\partial z}\frac{\partial z}{\partial x};\frac{\partial J}{\partial y}=\frac{\partial J}{\partial z}\frac{\partial z}{\partial y}$$

计算图 computational graph：指定了 BP 算子的输入和输出，刻画了变量之间的依赖，举例：

$$J=\frac{1}{1+e^{-(w_0+w_1{x}_1+w_2{x}_2)}}$$

可以画出计算图，先给出正向传播结果：

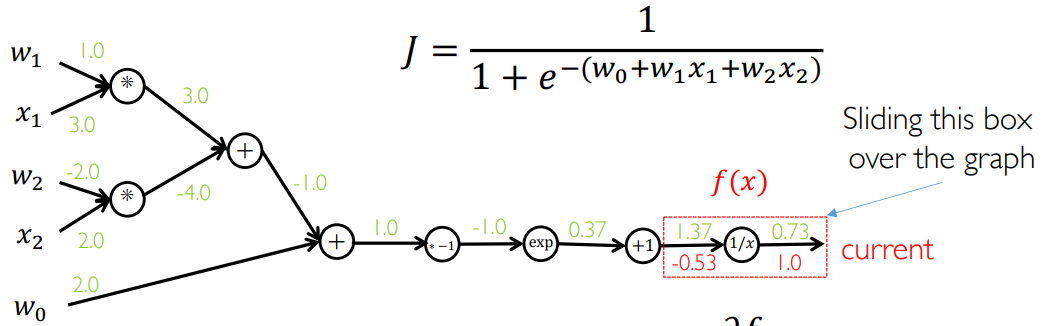
从最后一个算子算反向传播：

$$f(x)=\frac{1}{x}\to \frac{\partial f}{\partial x}=-\frac{1}{x^2}\to \frac{\partial J}{\partial x}=\frac{\partial J}{\partial f}\frac{\partial f}{\partial x}=1\times \frac{-1}{(1.37{)}^2}=-0.53$$

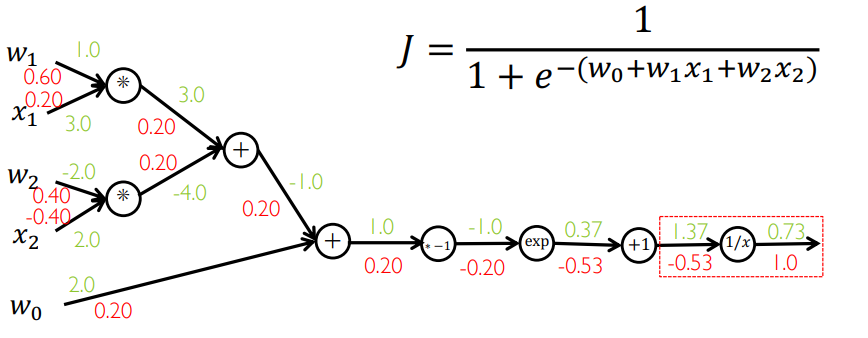
绿色为正向传播结果，红色为反向传播结果，需要将所有的中间结果保存在内存中，不能做优化！因此人们就利用求导的链式法则性质，提出了自动求导 AutoDiff。自动求导就是再构造一个（反向的）计算图，将所有的导函数放在计算图的节点上：

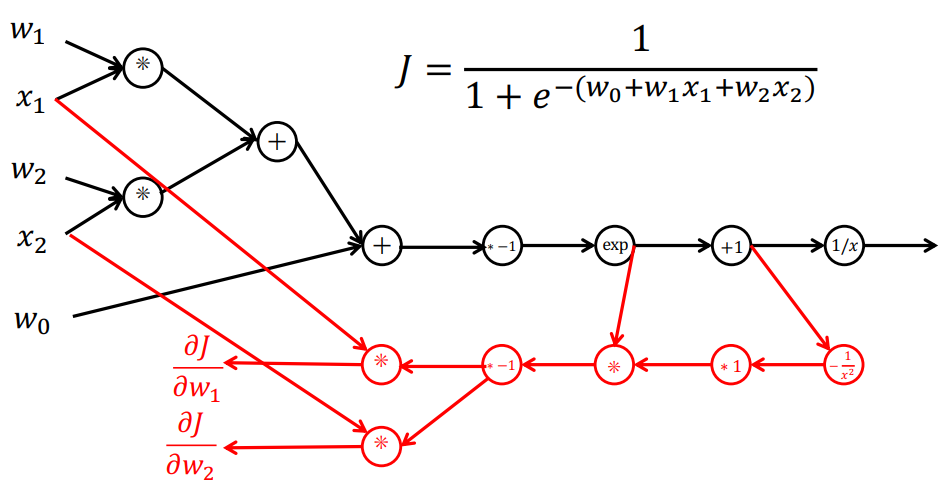
也就是说，直接经过这个导函数的计算图节点即可求出导函数的值：

• 对于 $J=f(x)=1/x$，关于 $x$ 的导数就是 $-1/x^2$，该单元输出为 $\partial J/\partial x$
• 对于 $y+1=x$，则关于 $y$ 的导数就是 $1$，$\partial x/\partial y=1$，该单元输出为 $\partial J/\partial y$
• 对于 $e^z=y$，则关于 $z$ 的导数就是 $e^z$ 自己，即 $\partial y/\partial z=e^z$，该单元输出为 $\partial J/\partial z$
• 对于 $u\ast (-1)=z$，则 $\partial z/\partial u=-1$，和上一个单元输入相乘（链式法则）得到 $\partial J/\partial u$
• 对于 $w_0+w_1{x}_1+w_2{x}_2=u$：
  • $\partial u/\partial w_1=x_1$，因此 $\partial J/\partial w_1=x_1\ast \partial J/\partial u$
  • $\partial u/\partial w_2=x_2$，因此 $\partial J/\partial w_2=x_2\ast \partial J/\partial u$
  • $\partial u/\partial w_0=1$，因此 $\partial J/\partial w_0=\partial J/\partial u$

那么以后我们自定义算子的时候，将前向计算和反向计算都写出来，写在程序里，就可以直接调用了。如何加速计算？研究图的拓扑排序，某个节点前的都可以并行计算。

例子：UW CSE 599W: Systems for ML. 陈天奇 XGBoost 的创立者：http://dlsys.cs.washington.edu/pdf/lecture4.pdf

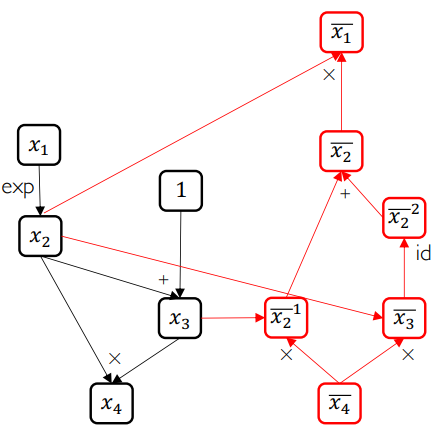
拓扑排序：将都不依赖别人的排在最前面。如图所示：

• $x_4=x_2\times x_3$
• $x_3=x_2+1$
• $x_2=\exp (x_1)$

因此按照求导的拓扑排序的话，应该是：

$$x_4\to x_3\to x_2\to x_1$$

自动求导：

$$\begin{array}{rl}& \frac{\partial J}{\partial x_4}=1\\ & \frac{\partial J}{\partial x_3}=\frac{\partial J}{\partial x_4}\frac{\partial x_4}{\partial x_3}=x_2\\ & \frac{\partial J}{\partial x_2}=\frac{\partial J}{\partial x_4}\frac{\partial x_4}{\partial x_2}+\frac{\partial J}{\partial x_3}\frac{\partial x_3}{\partial x_2}=x_3+x_2\\ & \frac{\partial J}{\partial x_1}=\frac{\partial J}{\partial x_2}\frac{\partial x_2}{\partial x_1}=(x_3+x_2)\exp (x_1)=(x_3+x_2)x_2\end{array}$$

对比反向传播算法和自动求导技术：自动求导的导函数算子都是内置的，只需要画出计算图即可，因此远远快于反向传播算法：

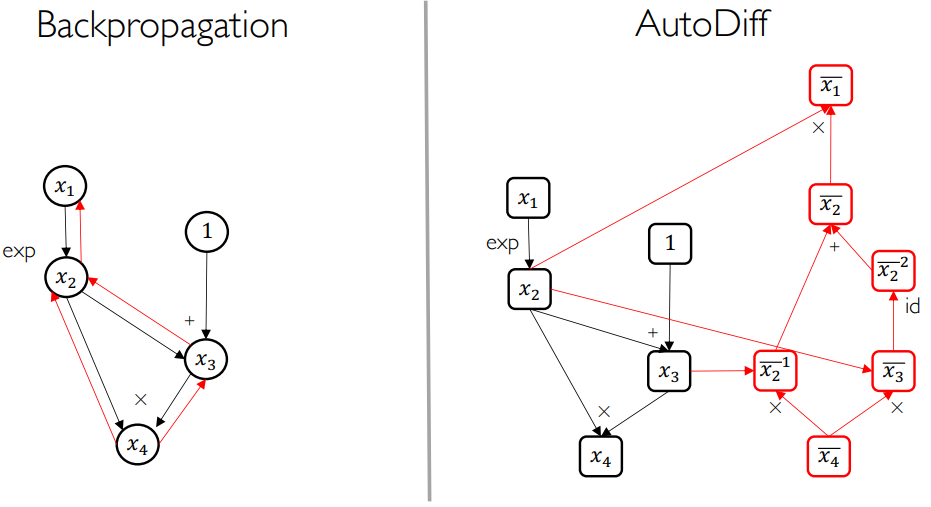
目前深度学习框架就是通过自动求导技术，全面加速神经网络的训练和计算。

• 2007 年，图灵奖得主发布了 theano 框架，实现了自动求导的简单版 2
• 2013 年，谷歌将 theano 变成商业可用的框架 Tensorflow，支持自动求导
• 2013 年，李沐提出了 mxnet 框架，后面还有很多类似的 Chainer、Keras
• 2016 年，百度做了飞桨 PaddlePaddle
• 2017 年，PyTorch 诞生
• 2018 年，清华提出了 Jittor 计图（计算图优化得越好就越快）

命令式 or 符号式。命令式比较好调试，如 PyTorch，符号式是写死了静态计算图，比较好优化。

2.6 实际中的训练技巧

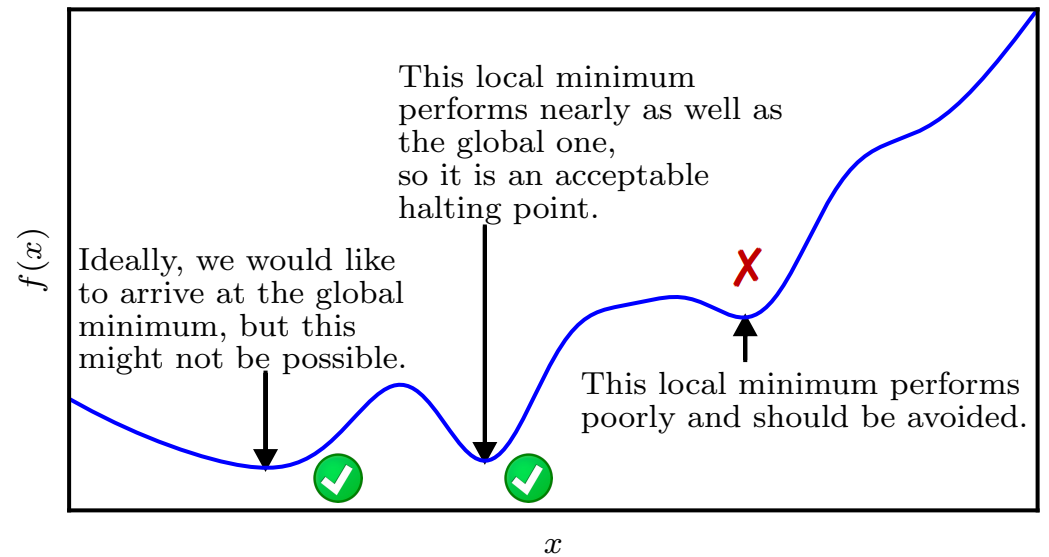
深度学习是一个非凸问题，因此找到比较好的全局极值是深度学习最重要的理论问题。推荐一篇论文：Y. Bengio. 的《Practical Recommendations for Gradient-Based Training of Deep Architectures. 》https://arxiv.org/pdf/1206.5533.pdf

2.6.1 随机梯度下降

不要计算全部输入训练对应的梯度了，而是每次从中取一个小批量 $m$ 来计算损失函数，从而计算样本梯度：

$$\begin{array}{rl}& \frac{\partial }{\partial {\theta }_{ij}^{(l)}}J(\theta ,b)=\frac{1}{m}\sum _{i=1}^m\frac{\partial }{\partial {\theta }_{ij}^{(l)}}J(\theta ,b;x^{(i)},y^{(i)})\\ & \frac{\partial }{\partial b_i^{(l)}}J(\theta ,b)=\frac{1}{m}\sum _{i=1}^m\frac{\partial }{\partial b_i^{(l)}}J(\theta ,b;x^{(i)},y^{(i)})\end{array}$$

• 计算代价小，超参数 $m$ 很重要，过大将会导致随机性变小
• 洗牌问题：一般来说为了保证数据的随机性，将数据集随机打散，按顺序取 $m$ 条
• 遍历 epoch：数据集完全扫描一次叫做一个 epoch，因此每个 epoch 之前都要洗牌
• 迭代 iteration：训练一次叫做一个 iteration，每次挑选 $m$ 条数据做 SGD 即可

$$\text{epoch}=\text{batchsize}\times \text{iteration}$$

2.6.2 含有冲量的随机梯度下降

随机梯度下降只是降低了计算成本，但不利于跳出局部极值。考虑生活中的冲量 Momentum 概念，假如你从山上往下跑，那么梯度会给你一个冲过头的量，也许能够克服局部极值。

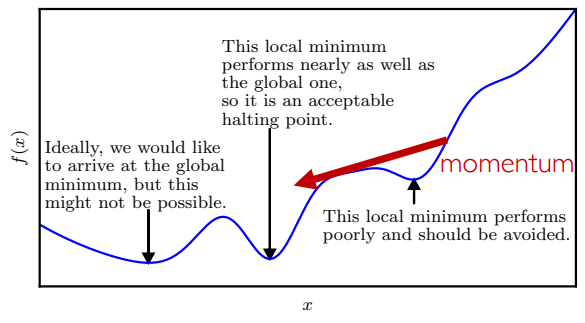
先算历史梯度的累积值（加权和）：

$$\mathrm{\Delta }=\beta \mathrm{\Delta }+\frac{\partial }{\partial {\theta }_i^{(l)}}J(\theta ,b)$$

如果 $\beta =1$，那就是历史梯度的直接求和。一般 $\beta \in [0,1]$，用于表示越远的梯度重要性越低，而越近的梯度影响程度越大 —— 指数滑动平均，也称 $\beta$ 为历史梯度重要性指数。例如第 $n$ 次的 $\mathrm{\Delta }$ 中的 ${\mathrm{\Delta }}_1$ 的系数就是 ${\beta }^{n-1}$。

$${\theta }_{ij}^{(l)}={\theta }_{ij}^{(l)}-\eta \mathrm{\Delta }$$

很多优化方法用了 SGD with Momentum，例如 RMSProp，ADAM。改进优化算法的核心：如何利用当前梯度信息获得更好的优化方向。冲量法是其中最有效也最简单的一种。

2.6.3 学习率衰减

学习率 $\eta$ 是一个相当重要的超参数。任何算法都需要调整学习率。学习率的调整包含两个部分：

• 初始学习率 ${\eta }_0$，一般取 $0.01$ 或 $0.001$
• 随着迭代进行，学习率应当衰减 —— 极值附近往往更加狭窄，因此我们需要降低学习速率。

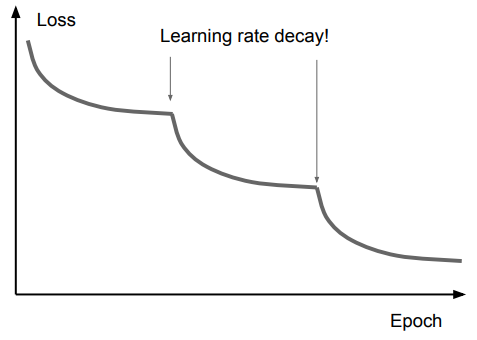
指数衰减：

$$\eta ={\eta }_0{e}^{-kt}$$

反比例衰减：

$$\eta =\frac{{\eta }_0}{1+kt}$$

固定步长衰减：每 $T$ 次迭代 iteration 衰减为原先的 $1/2$ 或者 $1/10$。

• 网络的层数越多，初始学习率越小
• 预训练模型的初始学习率也要很小，$0.001$ 或者更小
• 衰减策略：时间余弦衰减策略是目前 CNN 上效果最好的策略
• 大的学习率对应粗糙的特征，小的学习率对应学习更细粒度的特征

2.6.4 权重衰减

深度神经网络的函数族复杂，拟合能力强，因此很容易出现过拟合的现象。因此需要正则化方法，使得模型的函数族具有一定的正则性：

二范数正则化：

$$\mathrm{\Omega }(\theta )={\displaystyle \frac{\lambda }{2}}\sum _{l=1}^{n_{l-1}}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}({\theta }_{ji}^{(l)}{)}^2,\frac{\partial }{\partial {\theta }^{(l)}}\mathrm{\Omega }(\theta )=\lambda {\theta }^{(l)}$$

一范数正则化：

$$\mathrm{\Omega }(\theta )=\lambda \sum _{l=1}^{n_{l-1}}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}|{\theta }_{ji}^{(l)}|,\frac{\partial }{\partial {\theta }^{(l)}}\mathrm{\Omega }(\theta {)}_{ji}=\lambda (1_{{\theta }_{ji}^{(l)}>0}-1_{{\theta }_{ji}^{(l)}<0})$$

正则化项的加入能够控制假设空间的大小。深度学习一般将加入正则化方法称为权重衰减，虽然在传统机器学习中是一种主流方法，但是在深度学习中只是权重衰减无法很好地处理过拟合的问题。

2.6.5 随机丢弃

考虑一个全连接 MLP 网络，它的参数量过大，我们可以随机将每一层神经元的一半丢弃掉 dropout，那么对应的边和参数也就丢弃掉了，参加训练的参数量也减少了。实际中，将神经元的输入输出，以及对应边的权重全部置零。由于这是一个随机丢弃方法，每次迭代 iteration 丢弃的是不同的神经元，从宏观的角度来说，每一个神经元还是接受了训练。该方法由 Hinton 提出，有定理证明了，该方法等价于时间上的集成学习。因为每次遍历得到的模型其实是和而不同的。

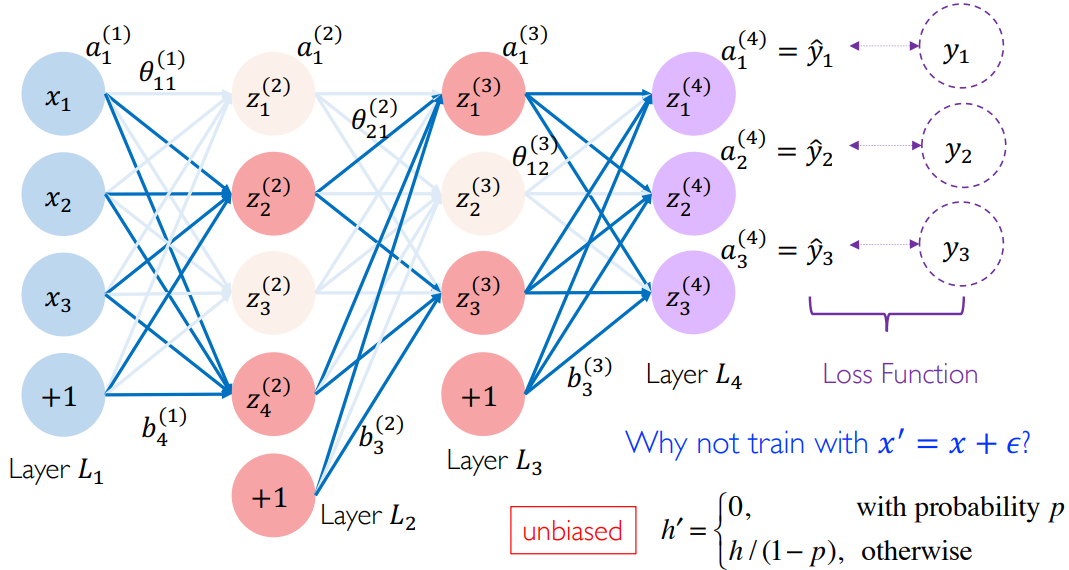
为了保证宏观意义上输出值的线性组合不变，因此要将剩下的神经元的激活值除以 $1-p$。

2.6.6 权重初始化

对于网络中参数而言，每个参数在刚开始时是不知道它们的值的，因此我们需要对参数做初始化。方法一般有两种：全部初始化为 0，或者随机初始化。而我们可以知道，有些优秀的局部极值我们是无法从 0 出发到达的，因此目前一般都是随机初始化。

深度学习中有一个重要结论：随着网络结构设计得越好，那么网络中局部极值的个数就越多。多到从任意点出发，我们稍微走几步就能到达一个较好的局部极值，前提是网络结构得设计好。

那么从什么分布中生成随机数呢？一般从高斯分布中生成随机数，高斯分布有两个参数，一个是均值，一个是方差，均值一般取 0 就可以了。至于方差，这个非常有讲究。目前来说有两种方差设置方法：

第一个是 Xavier 初始化方法，他将方差设置为：

$$\mathrm{Var}(w)=\frac{1}{n_{\text{in}}}$$

这个一般对应线性激活函数或者 Sigmoid 激活函数。

另一个是何恺明于 2015 年提出的初始化方法，他将方差设置为：

$$\mathrm{Var}(w)=\frac{2}{n_{\text{in}}}$$

这个一般对应 ReLU 激活函数，是深入研究了深度网络的结构后提出的。

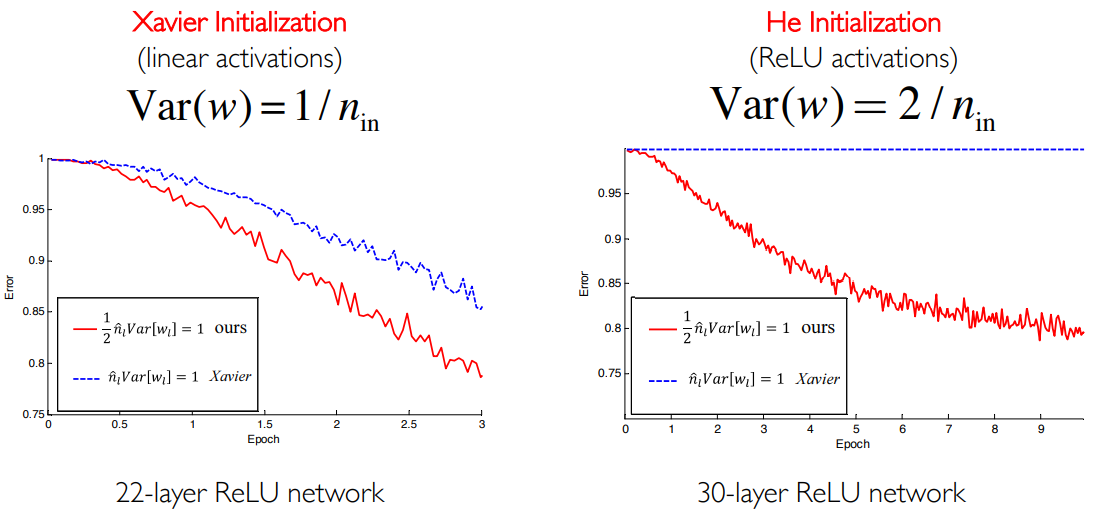
如图所示：在 22 层 ReLU 网络模型中，何的方法较 Xavier 方法有了一些提高；在 30 层 ReLU 网络模型中，Xavier 方法直接不下降了，而只有何的方法才会使得错误率降低。

两篇重要论文：

• Glorot X, Bengio Y. “Understanding the difficulty of training deep feedforward neural networks” JMLR, 2010, 9:249-256
• He K, Zhang X, Ren S, et al. “Delving Deep into Rectifiers: Surpassing Human-level Performace on ImageNet Classification”[J]. 2015:1026-1034

2.6.7 保姆级学习

由于神经网络的训练通常比较困难，因此需要做保姆级训练 Babysitting Learning，步骤如下：

• 在一个较小的数据集上实现过拟合：训练误差接近 0
• 观察到训练误差的抖动：不收敛，可能是学习率过大——初始学习率还是衰减速率？
  • 观察误差曲线：刚开始衰减还不错，那么可能是衰减速率不够快
  • 误差曲线一开始就抖动：初始学习率过大
• 发现某些神经元出现了饱和：没有得到更新
  • 网络的初始化没有做好/输入没有做好——过大，导致陷入饱和区
  • 调整好权重和激活值，何的方法或者 Xavier 方法设置的参数不容易使神经元陷入饱和区
  • 归一化方法处理激活值和输入值
  • 换用新的激活函数

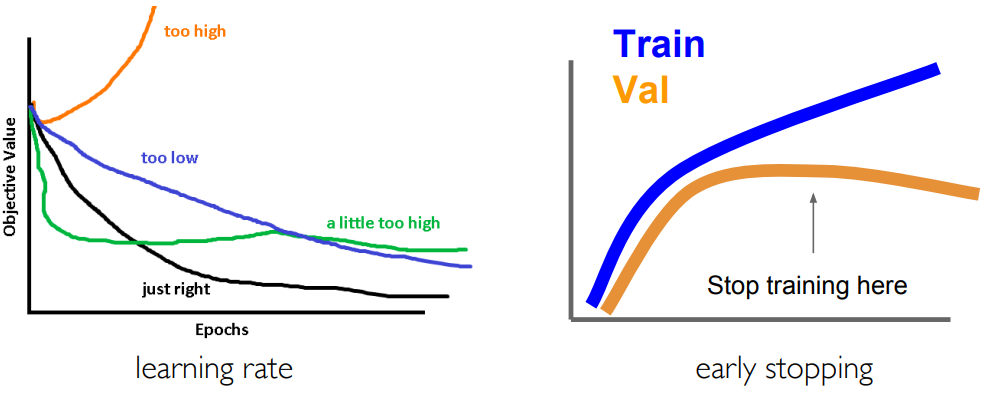
如图所示：

• 初始学习率过高：直接发散
• 初始学习率太低/衰减太慢：训练缓慢
• 不合适的学习率和衰减速率：绿色曲线，先快但是最终有很大的误差
• 合适的曲线：黑色线

观察验证集上的准确率：使用早停策略。神经网络如果无限训练下去，验证集准确率一定会先升后降。但是现在的高级神经网络训练技巧可以使得验证集误差变成渐近线，之后会学习。有人使用了高级的训练技巧，竟然使得残差网络的正确率逼近了 Transformer 模型！

多选题：以下哪些方法有助于深度网络跳出局部极值？

• 每轮遍历后，对数据进行重新洗牌：正确。随机梯度下降的核心，随机性有利于跳出鞍点。
• 每次迭代中，进行 2 次反向传播，更新 1 次梯度：反向传播如果不更新梯度，没有用。
• 在随机梯度下降中，引入冲量：正确。SGD with momentum 也可以冲过局部极值。
• 降低学习率：提高学习率才能越过局部极值。

深度学习是一门以实验为基础的学科。

2.7 通用逼近定理

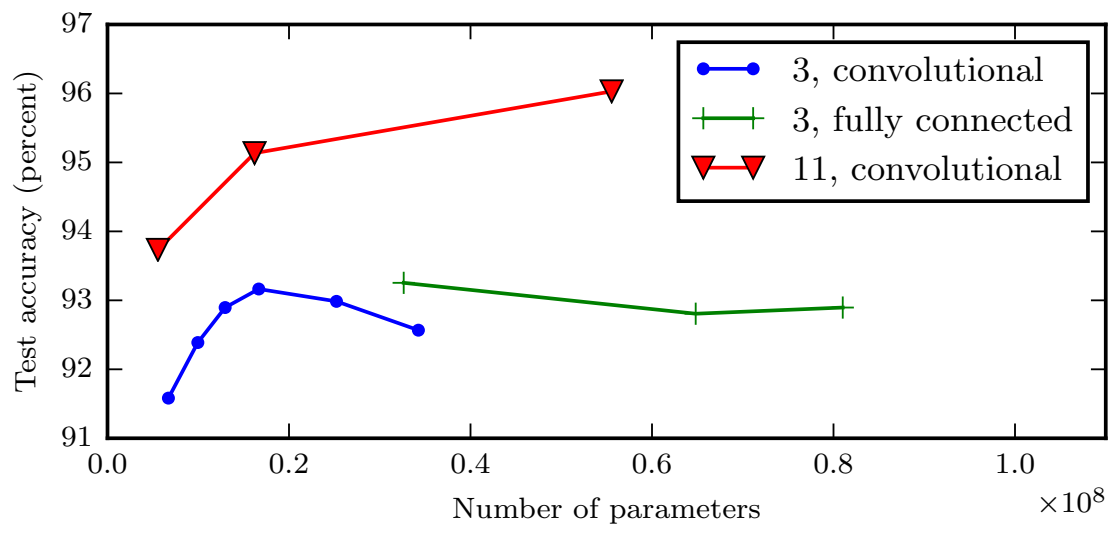
• 横轴：参数量；纵轴：测试准确率
• 参数量更大的全连接网络和参数量小的卷积网络正确率相当：网络结构的重要性
• 同样的网络结构而言：层数更深，准确率更高

2.7.1 万能逼近定理的两种形式

1991 年由 Hornik 和 Kurt 证明了万能逼近定理（任意深度情况）：$C(X,Y)$ 是从 $X$ 到 $Y$ 的一个函数族。设 $\sigma \in C(\mathbb{R}\mathbb{,}\mathbb{R})$ 是其中的一个函数，记 $(\sigma \circ x{)}_i=\sigma (x{)}_i$ 是一个逐元素操作的函数。如果 $\sigma$ 不是多项式，当且仅当：对整数 $n,m\in \mathbb{N}$，集合 $K\text{sub}{\mathbb{R}}^n$，任意函数 $f\in C(K,{\mathbb{R}}^m),\epsilon >0$。那么存在一个整数 $k\in \mathbb{N}$，以及三个矩阵：$A\in {\mathbb{R}}^{k\times n},b\in {\mathbb{R}}^k,W\in {\mathbb{R}}^{m\times k}$，使得：

$$\underset{x\in K}{sup}|f(x)-g(x)|<\epsilon$$

其中：$g(x)=W(\sigma \circ (Ax+b))$ 就是一个两层的 MLP 网络，它能表达任意的连续函数，注意此时的 $\sigma$ 不能是多项式函数。

万能逼近定理的另一个形式由北京大学的王立威老师证明（任意宽度情况）：对于 Bochner-Lebesgue 上 p-可积控制的函数 $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ 以及任意正整数 $\epsilon >0$，存在一个全连接的 ReLU 网络 $F$，并且它的宽度为（大于输入和输出维度） $d_m=max\{n+1,m\}$，满足：

$$\int |f(x)-g(x){|}^p\mathrm{d}x<\epsilon$$

此外，还存在一个函数 $f\in L^p({\mathbb{R}}^n,{\mathbb{R}}^m)$，如果一个 ReLU 网络宽度不够，那么上式不成立。也就是说，如果采用瓶颈层，理论上来说是不能完成逼近的。

2.7.2 浅层 MLP

虽然 Hornik 的万能逼近定理告诉我们：两层 MLP 可以逼近任意网络/决策面，但是他没有告诉你，这种情况下需要指数多个神经元，宽度是无限的。因此王立威老师的结论更强。

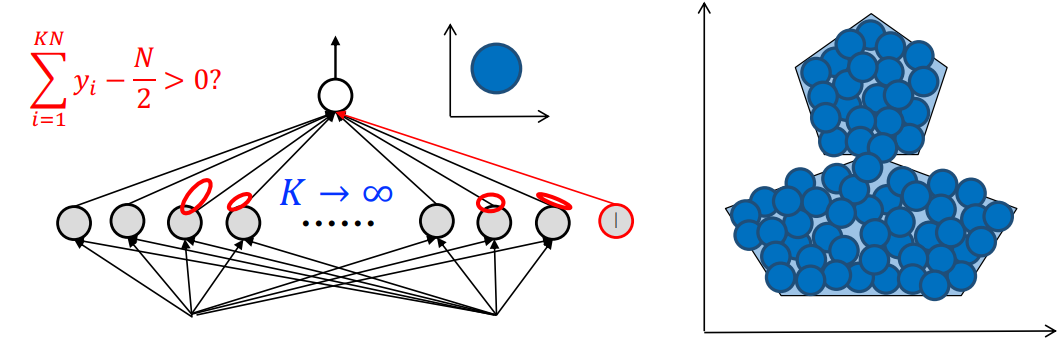
上节课我们说到：三层 MLP 是可以表示右图的，但是如果我们硬是要用两层 MLP 来表示的话，理论上也是可行的，但是却非常困难。首先要用两层 MLP 表示一个圆（凸多边形，“割圆术”，需要很多的神经元）这样的圆有很好的性质：圆内为正，圆外为 0，因此直接把所有的圆加起来，就得到了“或”的效果。因此这个网络就非常宽。

2.7.3 深度的作用

M Telgarsky 于 2016 年在 COLT 上发表《Benefits of depth in neural networks》证明了：对于任意正整数 $k$，那么存在一个层数为 $\mathrm{\Theta }(k^3)$，每层宽度为 $\mathrm{\Theta }(1)$ 的 ReLU 网络，这样的网络时不能被一个层数是 $\mathrm{\Theta }(k)$ 的网络所逼近（深层的函数族比浅层的函数族大），除非该浅层网络的宽度是 $\mathrm{\Omega }(2^k)$ 的。

2.7.4 宽度的作用

宽度显然也很重要，如果限制神经网络的宽度，那么复杂的决策面也是无法表示的。王立威团队于 2017 年在 NIPS 上发表《The Expressive Power of Neural Networks: A View from the Width》证明了：对于任意正整数 $k$，那么存在一个宽度为 $\mathcal{O}(k^2)$，深度为 2 的 ReLU 网络，它是不能被宽度为 $\mathcal{O}(k^{1.5})$，深度为 $k$ 的网络所逼近。

2.7.5 线性区域

由上述结论可知，我们在设计神经网络的时候需要不断地权衡网络的宽度和深度。Yoshua Bengio（深度学习三巨头之一）于 2014 年在 NIPS 上发表《On the number of linear regions of deep nerual networks》，其中指出：一个输入空间在神经元的操作之后相当于折叠。当我们把折叠后的区域舒展回来的时候，等价于对区域做了线性的划分（对应原始空间的很多个分散的小区域）：

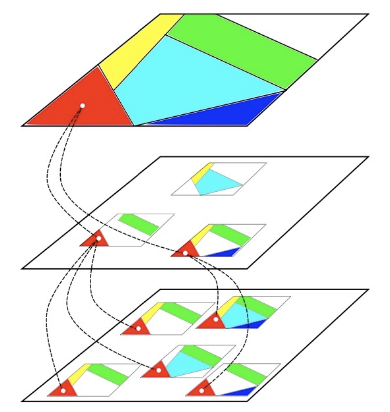
对于一个输入层是 $d$ 个神经元，$L$ 个隐藏层，每层的宽度（神经元个数）为 $n_i\ge d$ 的 ReLU 网络相当于：

$$\left(\prod _{i=1}^{L-1}{\lfloor {\displaystyle \frac{n_i}{d}}\rfloor }^d\right)\sum _{j=1}^d\left(\begin{array}{c}{n}_L\\ j\end{array}\right)$$

这么多个小的线性区域。证明在论文中有。简化：假设每层的神经元都有 $n$ 个，那么可以划分成的小的线性区域有：

$$\mathrm{\Omega }\left({\left({\displaystyle \frac{n}{d}}\right)}^{(L-1)d}{n}^d\right)$$

由于深度 $L$ 在指数上，宽度 $n$ 在底数上，因此所能表达的线性区域是宽度的深度次方。

2.7.6 凸多边形性质

Raghu 于 2017 年在 ICML 上发表了《On the expressive power of deep neural networks》文中指出：每一层的 ReLU 函数实际上就是把输入空间划分为凸多边形区域：

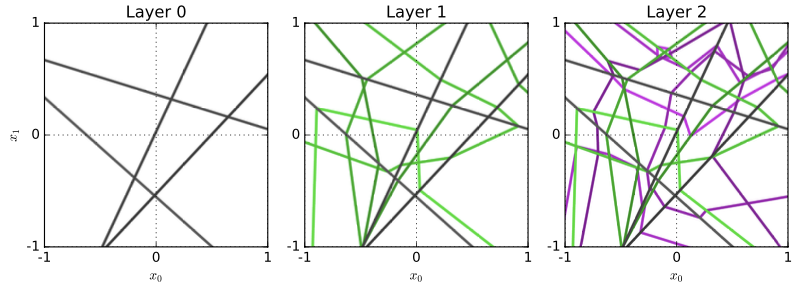
神经网络的决策面：输入空间划分为指数个凸多边形区域，并且打上标签，因此可以用来刻画很复杂、很精细的决策面。还有人指出：简单的输入函数经过网络的逐层变换可以得到复杂函数，复杂函数经过上述的逆过程可以得到简单函数。我们的人脸识别过程就是从右到左的过程：复杂问题转化为简单决策：


2.7.7 MLP 处理二维数据

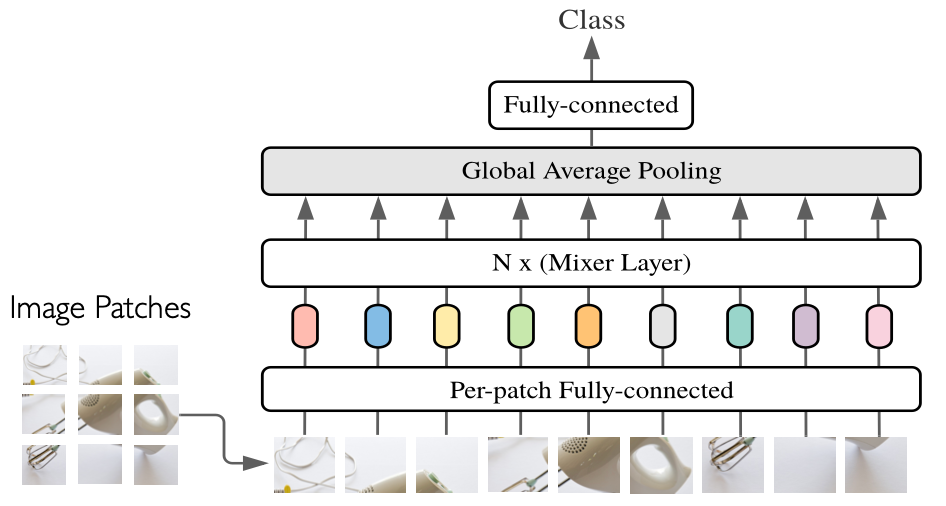
通用逼近定理决定了 MLP 网络可以逼近任意复杂函数——什么都可以干！很多高级模型都使用 MLP 网络，包括 AlphaGo，在用 CNN 提取完特征之后，就使用 MLP 网络进行学习。我们知道，MLP 网络的输入是处理一维数据的，那如果是 $n\times n$ 的二维数据，如图像，该如何处理呢？这个问题困扰了深度学习社区 20 年。

最早大家以为直接展开成一维数据，但是效果不好。CNN 的出现给了大家启发，我们可以把图像分为多个块 patch，例如每一块都是 $7\times 7$ 的小图像，将其展开为长度为 $49$ 的一维数据，这样就可以输入到 MLP 网络中了：

对于这 9 个块，我们如果把它们输入同一个 MLP 网络（参数都相同，也就是当作 9 个样本一次输入）那么自然结果不会好。而我们再引入多个 MLP 网络，重复上述操作，会得到不同的结果矩阵，矩阵的每一行有 9 个数，分别表示块的结果，列的数量就是引入的 MLP 网络的数量。一般把行称为 Tokens，列称为 Channels。

2.7.8 技术的螺旋上升