2286. 以组为单位订音乐会的门票

题目

一个音乐会总共有 n 排座位，编号从 0 到 n - 1 ，每一排有 m 个座椅，编号为 0 到 m - 1 。你需要设计一个买票系统，针对以下情况进行座位安排：

• 同一组的 k 位观众坐在 同一排座位，且座位连续 。
• k 位观众中 每一位 都有座位坐，但他们 不一定 坐在一起。

由于观众非常挑剔，所以：

• 只有当一个组里所有成员座位的排数都 小于等于 maxRow ，这个组才能订座位。每一组的 maxRow 可能 不同 。
• 如果有多排座位可以选择，优先选择 最小 的排数。如果同一排中有多个座位可以坐，优先选择号码 最小 的。

请你实现 BookMyShow 类：

• BookMyShow(int n, int m) ，初始化对象，n 是排数，m 是每一排的座位数。
• int[] gather(int k, int maxRow) 返回长度为 2 的数组，表示 k 个成员中 第一个座位 的排数和座位编号，这 k 位成员必须坐在 同一排座位，且座位连续 。换言之，返回最小可能的 r 和 c 满足第 r 排中 [c, c + k - 1] 的座位都是空的，且 r <= maxRow 。如果 无法 安排座位，返回 [] 。
• boolean scatter(int k, int maxRow) 如果组里所有 k 个成员 不一定 要坐在一起的前提下，都能在第 0 排到第 maxRow 排之间找到座位，那么请返回 true 。这种情况下，每个成员都优先找排数 最小 ，然后是座位编号最小的座位。如果不能安排所有 k 个成员的座位，请返回 false 。

示例 1：

输入：
["BookMyShow", "gather", "gather", "scatter", "scatter"]
[[2, 5], [4, 0], [2, 0], [5, 1], [5, 1]]
输出：
[null, [0, 0], [], true, false]

解释：
BookMyShow bms = new BookMyShow(2, 5); // 总共有 2 排，每排 5 个座位。
bms.gather(4, 0); // 返回 [0, 0]
                  // 这一组安排第 0 排 [0, 3] 的座位。
bms.gather(2, 0); // 返回 []
                  // 第 0 排只剩下 1 个座位。
                  // 所以无法安排 2 个连续座位。
bms.scatter(5, 1); // 返回 True
                   // 这一组安排第 0 排第 4 个座位和第 1 排 [0, 3] 的座位。
bms.scatter(5, 1); // 返回 False
                   // 总共只剩下 2 个座位。

提示：

• 1 <= n <= 5 * 10^4
• 1 <= m, k <= 10^9
• 0 <= maxRow <= n - 1
• gather 和 scatter 总 调用次数不超过 5 * 10^4 次。

解答

思路：线段树

需求分析，对某个数组 nums[1..n]

• 单点修改：时间复杂度为 $O(1)$
• 区间查询最小值/最大值：时间复杂度为 $O(n)$

这种方案维护的状态少，查询的速度慢。

另一个直观的想法就是，列举出它的所有子数组，同时每次修改都进行 维护：

• 单点修改 + 维护最值：时间复杂度为 $O(n^2)$
• 区间查询最小值/最大值：时间复杂度为 $O(1)$

这种方案维护的状态多，查询的速度快。

那么能否有 折中的方案 呢？同时降低维护的状态数和查询的速度，使他们降低到 $O(\log n)$ 的水平？

如图所示，假设我们的 n = 8，我们此时需要额外维护 4 个区间，但同时我们查询的时间复杂度从原先的 6 降低到了 3。如果再额外维护 2 个区间，那么查询的时间复杂度进一步降低到 2；如果最后再维护一个最大的区间，那么原先查询整个区间的时间复杂度 8 就变成了现在的 1 次查询。

• 单点修改的时间复杂度 = 维护的区间个数 $O(2n)$
• 区间查询最小值/最大值的时间复杂度 $O(\log n)$ 所查询 x 就是它二进制表示对应的区间

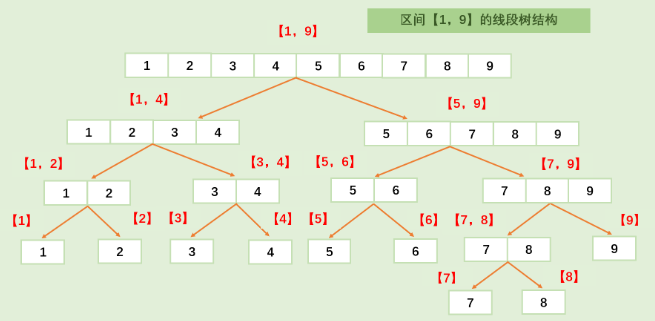
线段树的节点个数相当于一个满二叉树 + 不是满的最后一排，例如长度为 10 区间的线段树，它是由 1, 2, 4, 8 的满二叉树以及最后一排组成，假设最后一排也是满的，因此一共需要 31 个节点。例如，对于 $2^k\le n<2^{k+1}$ 的 $n$ 而言，线段树的节点个数为 $2^{k+2}-1$，因此开一个 $4n$ 长度的数组来表示线段树。

其实最优的数组长度不是 4n，而是 2 << n.bit_length()，例如这里就是 32

规定：

• 分割点是 左右端点和，除以 2 然后下取整
• 区间范围，数组下标都是从 1 开始的，这样方便计算

再谈区间查询的复杂度问题：

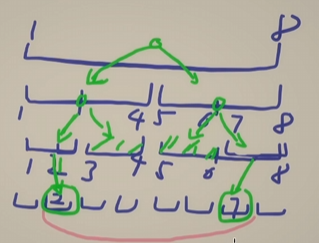
如图所示，假设我们要查询 2..7 区间，那么递归搜索树如图所示，我们从叶子节点回头看，除了递归的节点外，递归的节点的另一半都是直接返回的，因此时间复杂度就是递归次数，也就是树的高度 $\log n$。要么完全包含，要么继续往下递归。

代码：基本线段树

• 单点修改 $O(\log n)$
• 区间和查询 $O(\log n)$
• 区间最小值查询 $O(\log n)$

class BookMyShow:

    def __init__(self, n: int, m: int):
        self.n = n
        self.m = m
        self.sum = [0] * (4 * n)
        self.min = [0] * (4 * n)

    
    # self.add(1, 1, n, idx, val), nums[idx] += val
    def add(self, o: int, l: int, r: int, idx: int, val: int) -> None:
        if l == r:
            self.sum[o] += val  # o == idx
            self.min[o] += val 
            return
        
        mid = (l + r) // 2
        
        if idx <= mid:
            self.add(o * 2, l, mid, idx, val)          # 递归左子树
        else:
            self.add(o * 2 + 1, mid + 1, r, idx, val)  # 递归右子树
        
        self.sum[o] = self.sum[o * 2] + self.sum[o * 2 + 1]
        self.min[o] = min(self.min[o * 2], self.min[o * 2 + 1])


    # self.query_sum(1, 1, n, L, R), return [L, R] 返回内的元素和
    def query_sum(self, o: int, l: int, r: int, L: int, R: int) -> int:
        if L <= l and r <= R:
            return self.sum[o]  # 完全包含
        
        sum = 0
        mid = (l + r) // 2

        if L <= mid:
            sum += self.query_sum(o * 2, l, mid, L, R)
        
        if R > mid:
            sum += self.query_sum(o * 2 + 1, mid + 1, r, L, R)
        
        return sum
    

    # self.index(1, 1, n, R, val), return [1, R] 范围内 <= val 的最小下标，不存在为 0
    def index(self, o: int, l: int, r: int, R: int, val: int):
        if self.min[o] > val:
            return 0
        
        if l == r:
            return l
        
        mid = (l + r) // 2

        if self.min[o * 2] <= val:
            return self.index(o * 2, l, mid, R, val);
        
        if R > mid:
            return self.index(o * 2 + 1, mid + 1, r, R, val);
        
        return 0


    def gather(self, k: int, maxRow: int) -> List[int]:
        i = self.index(1, 1, self.n, maxRow + 1, self.m - k)

        if i == 0:
            return []
        
        seats = self.query_sum(1, 1, self.n, i, i)
        self.add(1, 1, self.n, i, k)

        return [i - 1, seats]

    
    # 总体复杂度 O((n + q)log n) q 表示前面的操作数，前面 gather 了多少次
    def scatter(self, k: int, maxRow: int) -> bool:
        left = (maxRow + 1) * self.m - self.query_sum(1, 1, self.n, 1, maxRow + 1)

        if left < k:
            return False
        
        i = self.index(1, 1, self.n, maxRow + 1, self.m - 1)

        while True:
            left_seats = self.m - self.query_sum(1, 1, self.n, i, i)

            if k <= left_seats:
                self.add(1, 1, self.n, i, k)
                return True
            
            k -= left_seats
            self.add(1, 1, self.n, i, left_seats)
            i += 1