2280. 表示一个折线图的最少线段数
题目
给你一个二维整数数组 stockPrices ,其中 stockPrices[i] = [dayi, pricei] 表示股票在 dayi 的价格为 pricei 。折线图 是一个二维平面上的若干个点组成的图,横坐标表示日期,纵坐标表示价格,折线图由相邻的点连接而成。比方说下图是一个例子:
请你返回要表示一个折线图所需要的 最少线段数 。
示例 1:
Python
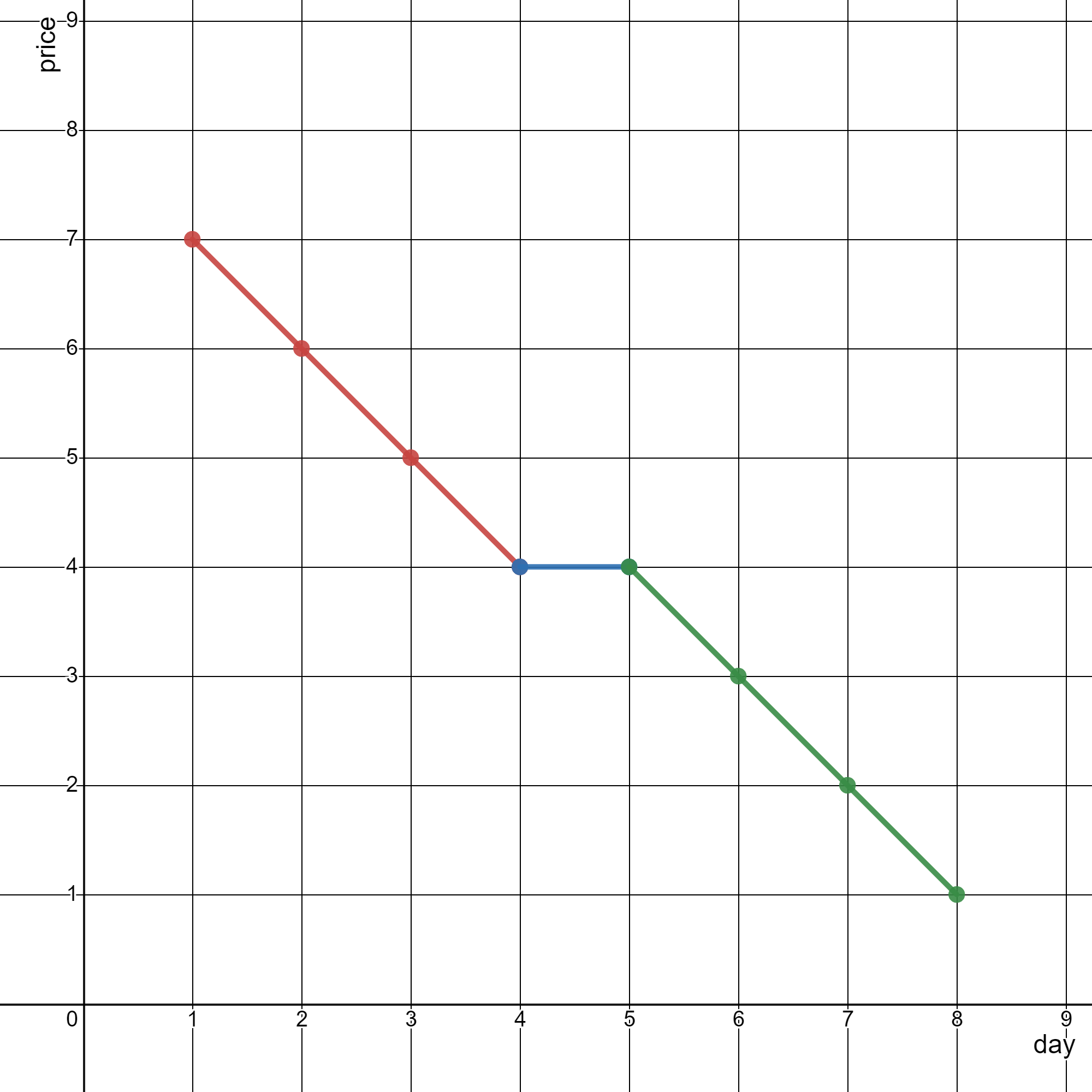
输入:stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
输出:3
解释:
上图为输入对应的图,横坐标表示日期,纵坐标表示价格。
以下 3 个线段可以表示折线图:
- 线段 1 (红色)从 (1,7) 到 (4,4) ,经过 (1,7) ,(2,6) ,(3,5) 和 (4,4) 。
- 线段 2 (蓝色)从 (4,4) 到 (5,4) 。
- 线段 3 (绿色)从 (5,4) 到 (8,1) ,经过 (5,4) ,(6,3) ,(7,2) 和 (8,1) 。
可以证明,无法用少于 3 条线段表示这个折线图。示例 2:
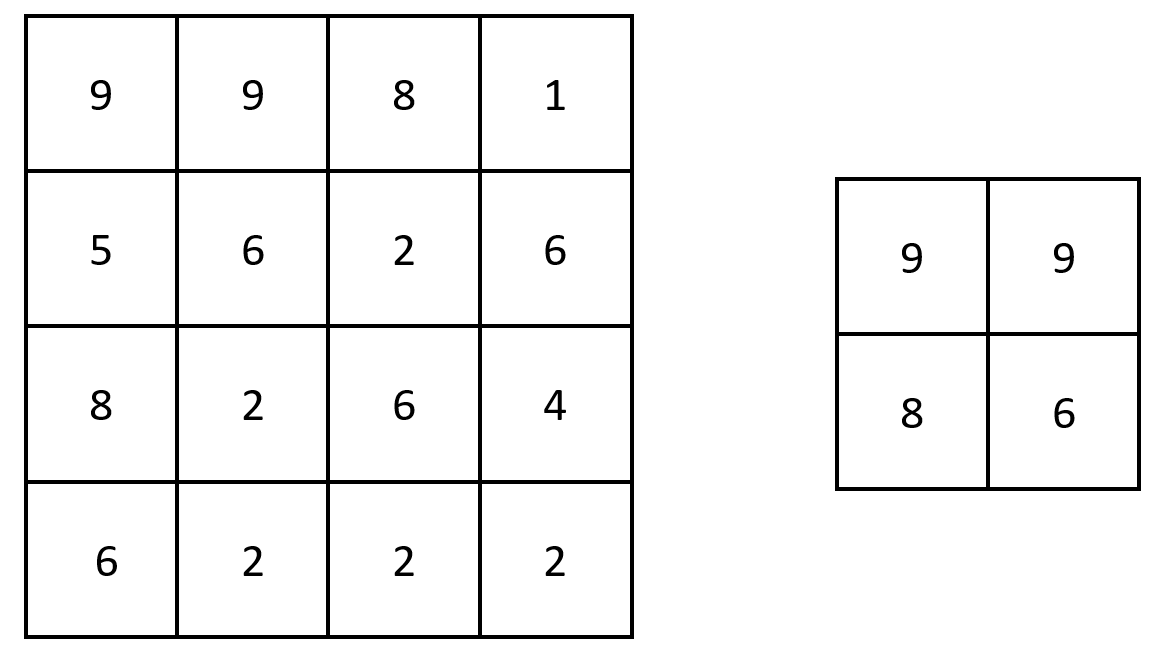
输入:stockPrices = [[3,4],[1,2],[7,8],[2,3]]
输出:1
解释:
如上图所示,折线图可以用一条线段表示。提示:
1 <= stockPrices.length <= 10^5stockPrices[i].length == 21 <= dayi, pricei <= 10^9- 所有
dayi互不相同 。
解答
思路
- 对
stockPrices[]按照第一个关键字排序 - 比较相邻的两个线段斜率是否相同
代码
python
# WA
class Solution:
def minimumLines(self, stockPrices: List[List[int]]) -> int:
s = stockPrices
s.sort()
n = len(s)
pre_k = inf
ans = 0
for i in range(1, n):
dx = s[i][0] - s[i - 1][0]
dy = s[i][1] - s[i - 1][1]
k = float(dy) / dx
if k != pre_k:
ans += 1
pre_k = k
return ans我们改用乘法:此时需要记录两个值,分别是 pre_dx, pre_dy:
python
class Solution:
def minimumLines(self, stockPrices: List[List[int]]) -> int:
s = stockPrices
s.sort()
n = len(s)
pre_dx = 0
pre_dy = 1 # 1 / 0 = inf
ans = 0
for i in range(1, n):
dx = s[i][0] - s[i - 1][0]
dy = s[i][1] - s[i - 1][1]
if dx * pre_dy != dy * pre_dx:
ans += 1
pre_dx = dx
pre_dy = dy
return ansC++ 可以用 long double 来写的,它的小数部分长度为 63 位,满足题目要求:
cpp
class Solution {
public:
int minimumLines(vector<vector<int>>& stockPrices) {
auto& s = stockPrices;
sort(s.begin(), s.end());
long double pre_k = 2e9;
int ans = 0;
for (int i = 1; i < s.size(); i ++) {
long double k = (long double)(s[i][1] - s[i - 1][1]) /
(s[i][0] - s[i - 1][0]);
if (k != pre_k) {
pre_k = k;
ans ++;
}
}
return ans;
}
};换成 double 是不行的,与 Python 是一样的。