2285. 道路的最大总重要性

题目

给你一个整数 n ，表示一个国家里的城市数目。城市编号为 0 到 n - 1 。

给你一个二维整数数组 roads ，其中 roads[i] = [ai, bi] 表示城市 ai 和 bi 之间有一条 双向 道路。

你需要给每个城市安排一个从 1 到 n 之间的整数值，且每个值只能被使用 一次 。道路的 重要性 定义为这条道路连接的两座城市数值 之和 。

请你返回在最优安排下，所有道路重要性 之和 最大 为多少。

示例 1：

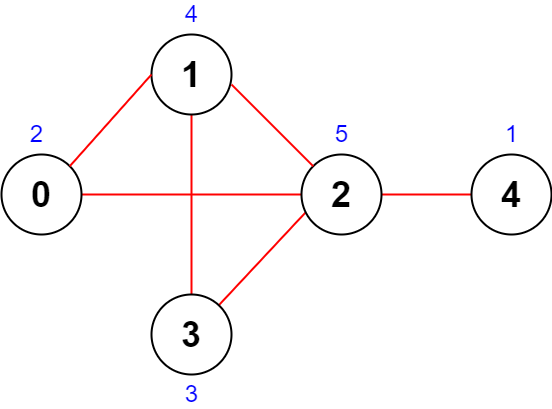
输入：n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
输出：43
解释：上图展示了国家图和每个城市被安排的值 [2,4,5,3,1] 。
- 道路 (0,1) 重要性为 2 + 4 = 6 。
- 道路 (1,2) 重要性为 4 + 5 = 9 。
- 道路 (2,3) 重要性为 5 + 3 = 8 。
- 道路 (0,2) 重要性为 2 + 5 = 7 。
- 道路 (1,3) 重要性为 4 + 3 = 7 。
- 道路 (2,4) 重要性为 5 + 1 = 6 。
所有道路重要性之和为 6 + 9 + 8 + 7 + 7 + 6 = 43 。
可以证明，重要性之和不可能超过 43 。

示例 2：

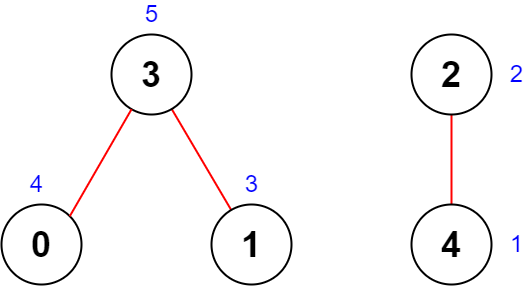
输入：n = 5, roads = [[0,3],[2,4],[1,3]]
输出：20
解释：上图展示了国家图和每个城市被安排的值 [4,3,2,5,1] 。
- 道路 (0,3) 重要性为 4 + 5 = 9 。
- 道路 (2,4) 重要性为 2 + 1 = 3 。
- 道路 (1,3) 重要性为 3 + 5 = 8 。
所有道路重要性之和为 9 + 3 + 8 = 20 。
可以证明，重要性之和不可能超过 20 。

提示：

• 2 <= n <= 5 * 10^4
• 1 <= roads.length <= 5 * 10^4
• roads[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi
• 没有重复道路。

解答

思路

考虑每个点对重要性的贡献，设点 $i$ 的度数为 ${\text{deg}}_i$，权重为 $p_i$，因此所有道路的重要性之和为：

$$\sum _i^n{\text{deg}}_i\times p_i$$

由于 deg[i] 实际上是从 roads[] 中可以求出的固定数组，p[i] 是从 $1\sim n$ 的数，这是可以自己设计的。因此根据 排序不等式 可知，最大的是顺序和：

排序不等式

如果 $a_1\le a_2\le \cdots \le a_n$ 和 $b_1\le b_2\le \cdots \le b_n$ 是两组实数，而 $a_{\sigma (1)},a_{\sigma (2)}\cdots ,a_{\sigma (n)}$ 是 $a_1,a_2,\cdots ,a_n$ 的一个随机排列。排序不等式指出：

$$a_1{b}_1+\cdots +a_n{b}_n\ge a_{\sigma (1)}{b}_1+\cdots +a_{\sigma (n)}{b}_n\ge a_n{b}_1+\cdots +a_1{b}_n$$

证明

首先我们知道，若 $x_i\le x_j,y_i\le y_j$，则有：

$$(x_j-x_i)(y_j-y_i)\ge 0$$

将上式展开并且移项得到：

$$x_i{y}_i+x_j{y}_j\ge x_j{y}_i+x_i{y}_j$$

我们设 $S_i$ 为原序列 $b_1,b_2,\cdots ,b_n$ 的前 $i$ 个数的和，即：

$$S_i=b_1+b_2+\cdots +b_i$$

设 $S_i^{\prime }$ 为打乱顺序后的排列 $b_{\sigma (1)},b_{\sigma (2)}\cdots ,b_{\sigma (n)}$ 的前 $i$ 个数的和，由于 $b_1\le b_2\le \cdots \le b_n$，所以 $S_i$ 也是序列最小的 $i$ 个数之和。因此有 $S_i\le S_i^{\prime }$。这里设 $S_0=0$。

注意到：

$$\sum _{k=1}^n{a}_k{b}_k=\sum _{k=1}^n{a}_k(S_k-S_{k-1})=\sum _{k=1}^{n-1}{S}_k(a_k-a_{k+1})+S_n{a}_n$$

同时：

$$\sum _{k=1}^n{a}_k{b}_{\sigma (k)}=\sum _{k=1}^n{a}_k(S_k^{\prime }-S_{k-1}^{\prime })=\sum _{k=1}^{n-1}{S}_k^{\prime }(a_k-a_{k+1})+S_n^{\prime }{a}_n(S_n^{\prime }=S_n)$$

注意到 $a_i-a_{i+1}\le 0$，则 $S_i(a_i-a_{i+1})\ge S_i^{\prime }(a_i-a_{i+1})$，因此当 $n$ 时：

$$\sum _{k=1}^n{a}_k{b}_k=\sum _{k=1}^{n-1}{S}_k(a_k-a_{k+1})+S_n{a}_n\ge \sum _{k=1}^{n-1}{S}_k^{\prime }(a_k-a_{k+1})+S_n^{\prime }{a}_n=\sum _{k=1}^n{a}_k{b}_{\sigma (k)}$$

同理可以设 $T_i$ 为 $b_n,b_{n-1},\cdots ,b_1$ 也就是倒序的前 $i$ 个数的和。那么显然有 $S_i\le S_i^{\prime }\le T_i$，因为 $T_i$ 是序列最大的 $i$ 个数之和。这里也设 $T_0=0$ 方便计算。

则有：

$$S_i(a_i-a_{i+1})\ge S_i^{\prime }(a_i-a_{i+1})\ge T_i(a_i-a_{i+1})$$

加之：

$$\sum _{k=1}^n{a}_k{b}_{n+1-k}=\sum _{k=1}^n{a}_k(T_k-T_{k-1})=\sum _{k=1}^{n-1}{T}_k(a_k-a_{k+1})+T_n{a}_n(T_n=S_n)$$

因此：

$$\sum _{k=1}^n{a}_k{b}_k\ge \sum _{k=1}^n{a}_k{b}_{\sigma (k)}\ge \sum _{k=1}^n{a}_k{b}_{n+1-k}$$

证毕。

思路：贪心之邻项交换

除了排序不等式，更直观的就是一种贪心思想：邻项交换。

假设现在有 $d_1\le d_2,p_1<p_2$，由于：

$$d_1{p}_1+d_2{p}_2-(d_1{p}_2+d_2{p}_1)=(d_1-d_2)(p_1-p_2)\ge 0$$

也就是说如果把较小的 $p_1$ 赋值给更大度数的点，不会得到更优的结果，这里也有一点抽屉原理的意思。既然不会得到更优的结果，那么按照 $d_i$ 的大小顺序赋值即可。

代码

class Solution:
    def maximumImportance(self, n: int, roads: List[List[int]]) -> int:
        deg = [0] * n
        
        for x, y in roads:
            deg[x] += 1
            deg[y] += 1
        
        deg.sort()

        return sum(d * i for i, d in enumerate(deg, 1))