2281. 巫师的总力量和

题目

作为国王的统治者，你有一支巫师军队听你指挥。

给你一个下标从 0 开始的整数数组 strength ，其中 strength[i] 表示第 i 位巫师的力量值。对于连续的一组巫师（也就是这些巫师的力量值是 strength 的 子数组），总力量 定义为以下两个值的 乘积 ：

• 巫师中 最弱 的能力值。
• 组中所有巫师的个人力量值 之和 。

请你返回 所有 巫师组的 总 力量之和。由于答案可能很大，请将答案对 10^9 + 7 取余 后返回。

子数组 是一个数组里 非空 连续子序列。

示例 1：

输入：strength = [1,3,1,2]
输出：44
解释：以下是所有连续巫师组：
- [1,3,1,2] 中 [1] ，总力量值为 min([1]) * sum([1]) = 1 * 1 = 1
- [1,3,1,2] 中 [3] ，总力量值为 min([3]) * sum([3]) = 3 * 3 = 9
- [1,3,1,2] 中 [1] ，总力量值为 min([1]) * sum([1]) = 1 * 1 = 1
- [1,3,1,2] 中 [2] ，总力量值为 min([2]) * sum([2]) = 2 * 2 = 4
- [1,3,1,2] 中 [1,3] ，总力量值为 min([1,3]) * sum([1,3]) = 1 * 4 = 4
- [1,3,1,2] 中 [3,1] ，总力量值为 min([3,1]) * sum([3,1]) = 1 * 4 = 4
- [1,3,1,2] 中 [1,2] ，总力量值为 min([1,2]) * sum([1,2]) = 1 * 3 = 3
- [1,3,1,2] 中 [1,3,1] ，总力量值为 min([1,3,1]) * sum([1,3,1]) = 1 * 5 = 5
- [1,3,1,2] 中 [3,1,2] ，总力量值为 min([3,1,2]) * sum([3,1,2]) = 1 * 6 = 6
- [1,3,1,2] 中 [1,3,1,2] ，总力量值为 min([1,3,1,2]) * sum([1,3,1,2]) = 1 * 7 = 7
所有力量值之和为 1 + 9 + 1 + 4 + 4 + 4 + 3 + 5 + 6 + 7 = 44 。

示例 2：

输入：strength = [5,4,6]
输出：213
解释：以下是所有连续巫师组：
- [5,4,6] 中 [5] ，总力量值为 min([5]) * sum([5]) = 5 * 5 = 25
- [5,4,6] 中 [4] ，总力量值为 min([4]) * sum([4]) = 4 * 4 = 16
- [5,4,6] 中 [6] ，总力量值为 min([6]) * sum([6]) = 6 * 6 = 36
- [5,4,6] 中 [5,4] ，总力量值为 min([5,4]) * sum([5,4]) = 4 * 9 = 36
- [5,4,6] 中 [4,6] ，总力量值为 min([4,6]) * sum([4,6]) = 4 * 10 = 40
- [5,4,6] 中 [5,4,6] ，总力量值为 min([5,4,6]) * sum([5,4,6]) = 4 * 15 = 60
所有力量值之和为 25 + 16 + 36 + 36 + 40 + 60 = 213 。

提示：

• 1 <= strength.length <= 10^5
• 1 <= strength[i] <= 10^9

解答

思路

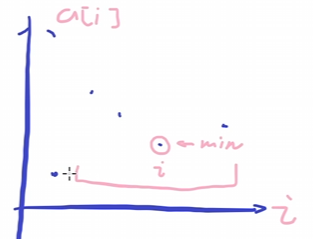
如图所示，假设巫师的能力值 strength[i] 画在了图上，因此对于其中的某个 strength[i]，我们关注它到底是 哪些子数组 的最小值。从图中可以看出，我们要找到的就是：

• 前一个最靠近它且比它小的数：上一个更小的数
• 后一个最靠近它且比它大的数：下一个更小的数

而这正是单调栈模型。假设我们对于 [1, 7, 6, 4, 5] 依次要找到它的下一个更小的数：

nums = 
      [1, 7, 6, 4, 5]
ans = []              # stk = [1]
ans = []              # stk = [1, 7]
ans = [N, 6]          # stk = [1, 6] 此时由于 7 已经找到答案了，因此直接删掉
ans = [N, 6, 4]       # stk = [1, 4]
ans = [N, 6, 4]       # stk = [1, 4, 5]